



suivant: Integration
monter: Derivative and partial derivative
précédent: Derivative and first order
Table des matières
Index
Derivative and n-th order
partial derivative : diff derive deriver
derive (or diff) may take more than two arguments : an
expression and the names of the derivation variables (each variable
may be followed by $n to indicate the number n of derivations).
diff returns the partial derivative of the expression with respect to
the variables given after the first argument.
The notation $ is usefull if you want to derive k times with
respect to the same variable, instead of entering k times the
same variable name, one enters the variable name followed by $k,
for example x$3 instead of (x,x,x).
Each variable may be followed by a $, for example
diff(exp(x*y),x$3,y$2,z) is the same as
diff(exp(x*y),x,x,x,y,y,z)
Examples
- Compute :
Input :
diff(x*y ^2*z^3+x*y*z,x,z)
Output :
y^2*3*z^2+y
- Compute :
Input :
diff(x*y ^2*z^3+x*y*z,x,z,z)
Or input :
diff(x*y ^2*z^3+x*y*z,x,z$2)
Output :
y^2*3*2*z
- Compute the third derivative of :
Input :
normal(diff((1)/(x^2+2),x,x,x))
Or :
normal(diff((1)/(x^2+2),x$3))
Output :
(-24*x^3+48*x)/(x^8+8*x^6+24*x^4+32*x^2+16)
Remark




suivant: Integration
monter: Derivative and partial derivative
précédent: Derivative and first order
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
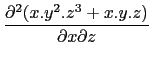
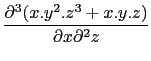
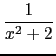
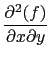 and
and