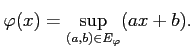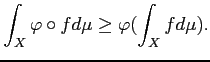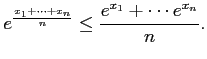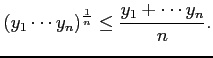Exercice 1.1 Dans cet exercice on suppose que
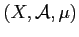
est
un espace mésuré tel que
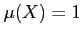
et
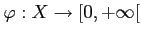
est une fonction connvexe, i. e.,
- Montrer que la fonction
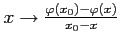 est croissante.
est croissante.
- On pose
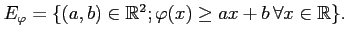 Montrer que
Montrer que
- En déduire que si
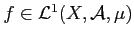 ,
alors
,
alors
- En déduire que si
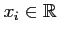 alors
alors
- En déduire que si
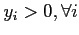 alors on a
alors on a