Topological Methods For The Study Of Discrete Structures

1.  Dates

From March 1st to March 5th, 2010.

2.  Description of the week

This week will focus on the use of tools coming from topology for the study of discrete structures like graphs, clouds of points,... For example, homology is a well-known concept from topology, which can be applied to combinatorial problems: the idea is to associate with a combinatorial object some simplicial complex, so that, by computing its homology, one gets informations on combinatorial properties of the original object.

The main lectures of this week will focus on

• Topological methods for combinatorics
• Topological methods for discrete geometry
• Persistence and homology computation

There will be an introductory course about homology on Monday.

Note that this week, the last one of the thematic month, is followed by a (one-week) conference on computational geometry geometry organized by Éric Colin de Verdière and Boris Thibert, from 08-03 to 12-03. Participants of both weeks can thus also interact.

3.  Confirmed morning lectures (4h30 each)

• Ron Aharoni: Connectivity, colorability and matchability.

Abstract: Hypergraphs (namely sets of sets, the latter being called "edges") can be realized geometrically: every vertex is represented by a point in Rn and every edge is represented by a "simplex", which is plainly the convex hull of the points corresponding to its vertices. (There is a simple requirement – no intersections between simplices should exist that do not follow from the intersection of the edges themselves. But this is easy to obtain if n is high enough.) The realization is called a "simplicial complex" It is usually demanded that the complex is closed downwards, so we shall always assume that the original hypergraph has this property. A closed down hypergraph is suitably called an abstract complexes, or also plainly a complex. Surprisingly, the properties of the geometric realization can sometimes shed light on combinatorial properties of the abstract complex. In particular, one property containing important information is the connectivity of the complex. This is the dimension of the lowest dimensional "hole" in the complex, namely an image of Sn that cannot be filled by simplices from the complex. From the combinatorial point of view, connectivity of order k means being able to move continuously between edges of size up to k. Combinatorial usage of the notion of connectivity usually consists of two parts: 1. showing how properties of the abstract complex follow from high connectivity of the geometrical complex, and 2. proving lower bounds on the connectivity in terms of combinatorial parameters. In the talks I will discuss two applications – the Lovasz lower bound on the chromatic number of a graph in terms of the connectivity of the neighborhood complex of the graph, and my extension with P. Haxell of Hall's theorem. Most of the talks will be concerned with the latter, and its various applications.

• Herbert Edelsbrunner: Persistence Homology, Algorithms, and Applications

Abstract: In this series of three lectures, I will introduce the concept of persistent homology, discuss algorithms, and present applications. A. Homology and Persistent Homology. Homology groups belong to the oldest topics in Algebraic Topology, dating back to the founding years. Persistence is a recent addition to the theory, motivated by practical needs that clash with the instability of homology computations for noisy data. In contrast, persistence is stable in a sense we will make precise in this first lecture. B. Matrix Reduction Algorithms. The classic algorithm for computing homology works by reduction of the boundary matrices to Smith normal form. A variant of this algorithm can be used to get the rich collection of persistence information of a filtration within about the same amount of time. There are fast implementations for important special cases, including functions on 2-manifolds. C. Applications. Persistent homology quantifies scale through a measure of the features in a discrete or continuous structure. It has been used to prove new mathematical theorems, to analyze scientific datasets, and to generally shed light on multiscale phenomena in nature.

• Konstantin Mischaikow : Computational Topology and Dynamics

Abstract:The focus of these lectures is on the use of computational topology to obtain coarse robust global descriptions of nonlinear dynamics. A rough breakdown of the topics is as follows: Lecture 1: We will begin with the definitions of homology groups of spaces and the homorphisms induced by continuous maps. We will then discuss methods for computing these quantities. Lecture 2: We will give a brief introduction to dynamical systems and bifurcation theory. The focus is on why algebraic topological methods are crucial for applications. We will then discuss isolating neighborhoods, attractor-repeller pairs, and Morse decompositions in the context of the decomposition of dynamics and discuss the computation of these objects. Lecture 3: We will define and discuss the Conley index as a algebraic tool to understand the structure of invariant sets. We will conclude with applications to a variety of different types of problems.

4.  Schedule for the morning lectures

	Lundi	Mardi	Mercredi	Jeudi	Vendredi
9h-10h30	Aharoni	Edelsbrunner	Mischaikow	Edelsbrunner	-
11h-12h30	Mischaikow	Aharoni	Edelsbrunner	Aharoni	Mischaikow

5.  Currently uploaded slides

6.  Participants

See the page http://www.lirmm.fr/~monteil/participants-week-5.html

7.  Proposed workshops (add your suggestions here)

• People from the ANR project "Graphs through Topological Structures": The topological meaning of the Colin-de-Verdiere invariant 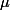defined for graphs (and other similar parameters)
• Pavle Blagojevic : "Topological methods in geometric combinatorics with the view toward open problems"
• Pedro Real: 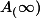-algebras, homological trees, and digital images";
• Javier Carnero Iglesias.
• Nicolas Delanoue. Guaranteeing the homotopy type of a set defined by non-linear inequalities.
• Samuel Peltier and Guillaume Damiand: Presentation of a cellular combinatorial structure used in geometric modeling, generalized maps, and its use in homology computation
• Christian Mercat: "Discrete Complex Analysis" How to turn a weighted graph into a discrete Riemann structure and how far the analogy goes (very far!).
• Eli Berger : Cake slicing and wait-free synchronizing.
• Francis Sergeraert: Discrete vector fields in algebraic topology.
• Pawel Dlotko: Homology and cohomology reduction algorithms and applications.