MIAS2 TP3
Méthode de Newton

Rappels
Pour résoudre l'équation f (x) = 0 lorsque f est suffisamment régulière, on itère la fonction :

g(x) = x - $${\frac{f(x)}{f'(x)}}$$

On a :

g'(x) = $${\frac{f(x).f''(x)}{f'(x)^2}}$$

donc si a est un zéro de f et n'est pas un zéro de f' :

g(a) = a,    g'(a) = 0

et a est un point fixe de g qui annule g'. Lorsque la suite des itérées de g ( u_n = g(u_{n - 1})) converge (ce sera le cas si on part d'un u₀ suffisamment proche de a), alors elle converge de façon quadratique :

| u_n - a| $$\leq$$ k| u_{n - 1} - a|²

parce que g'(a) = 0, alors que pour une suite qui vérifie seulement les hypothèses du théorème du point fixe, la convergence est moins rapide (linéaire) :

| u_n - a| $$\leq$$ k| u_{n - 1} - a|,    k < 1

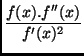
Exemple: l'algorithme de Héron Cet algorithme, basé sur la méthode de Newton, permet de déterminer des valeurs approchées de racines d'entiers.
Pour calculer une valeur approchée de $\sqrt{b}$ où b > 1, on pose :

$${\textstyle\frac{1}{2}} {\frac{b}{u_{n-1}}}$$ (1)

Exercice (à faire en TD)
Justifiez la convergence quadratique de la suite u_n de (1) vers $\sqrt{b}$. Indication, montrer que :

$$\sqrt{b} \leq \leq \sqrt{b} {\frac{(u_{n-1}-\sqrt{b})^2}{2u_{n-1}}}$$ (2)

-/-

On rappelle qu'on a programmé au TP2 une fonction iter(f,a,N,epsilon) qui calcule les valeurs successives de la suite u_n définie par u₀ et u_{n + 1} = f (u_n) et s'arrête lorsque | u_{n + 1} - u_n| < $\varepsilon$ ou lorsque n > N.

Exercice 1 (à rendre à la fin de la séance)
Déterminez avec la fonction iter pour quelles valeurs de n, on a

| u_{n + 1} - u_n| < 10^-4,    | u_{n + 1} - u_n| < 10^-8

pour la suite de Héron pour b = 2 et pour la suite récurrente définie par

u₀ = 1,    u_{n + 1} = $${\frac{u_n+2}{u_n+1}}$$

N.B.: les justifications de convergence vers $\sqrt{2}$ font l'objet de l'exercice 3.

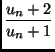
Exercice 2 (à rendre à la fin de la séance)
Appliquez la méthode de Newton pour résoudre x⁴ - 6 = 0, On donnera la suite récurrente u_n correspondante, une valeur initiale, le résultat de la fonction iter avec $\varepsilon$ = 10^-10, et on justifiera rigoureusement que la suite est convergente.

Exercice 3 (à rendre au début de la séance suivante)
Justifier que les deux suites de l'exercice 1 satisfont les hypoyhèses du théorème du point fixe sur [1, 2] (vous pouvez utiliser un logiciel de calcul formel pour faire les calculs!). Donnez alors une majoration de | u_{n + 1} - $\sqrt{2}$| dans les deux cas pour n tel que | u_{n + 1} - u_n| < 10^-7 (utilisez la majoration | u_n - $\sqrt{2}$| $\leq$ ${\frac{\vert u_{n+1}-u_n\vert}{1-k}}$ où k est la constante du théorème du point fixe et utilisez (2) pour la suite de Héron). Justifiez l'intérêt de la méthode de Newton.

Exercice 4 (à rendre au début de la séance suivante)
Programmez la méthode de Newton pour trouver une racine d'un polynôme P à coefficients complexes (on écrira une fonction racine(P,a,N,epsilon) où P désigne le polynôme, a la valeur initiale de la suite récurrente, N le nombre maximal d'itérations et le test d'arrêt du programme sera | u_{n + 1} - u_n| < $\varepsilon$).
Vérifiez votre programme avec le polynôme x⁴ - 6 et une valeur de départ proche du $\sqrt[4]{6}$.
Testez votre programme avec x⁴ + 1 et plusieurs valeurs de départ (essayez d'en trouver une pour chacune des racines complexes de x⁴ + 1), expliquez pourquoi il faut donner une valeur de départ non réelle pour espérer converger vers une racine de ce polynôme.