


suivant: À propos de ce
monter: Méthode itératives
précédent: Méthode des itérations inverses.
Soit
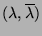 le couple de valeurs propres
correspondant au couple de vecteurs propres
le couple de valeurs propres
correspondant au couple de vecteurs propres
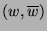 .
Montrer que
.
Montrer que 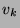 s'approche de
l'espace vectoriel engendré par
s'approche de
l'espace vectoriel engendré par 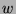 et
et 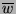 . En déduire que
. En déduire que
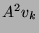 est approximativement combinaison linéaire à coefficients
réels de
est approximativement combinaison linéaire à coefficients
réels de 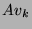 et
et 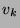 lorsque
lorsque 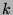 est grand :
est grand :
Exercice 6 (à rendre au plus tard le jour de l'examen)
Trouver le couple de valeurs propres de plus grand module de la matrice :
Faites de même pour le couple de plus petit module.
2003-02-19
