


suivant: Méthode des itérations inverses.
monter: Méthode itératives
précédent: Méthode itératives
Méthode de la puissance.
La méthode de la puissance est une méthode numérique qui permet de
déterminer la valeur propre de module maximal d'une matrice à coefficients
réels (en supposant que 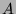 possède
une seule valeur propre de module maximal qui est alors réelle).
On prend un vecteur
colonne
possède
une seule valeur propre de module maximal qui est alors réelle).
On prend un vecteur
colonne 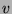 au hasard et on calcule la suite récurrente:
au hasard et on calcule la suite récurrente:
Si la composante de  sur l'espace propre correspondant à la valeur
propre de plus grand module n'est pas nulle,
sur l'espace propre correspondant à la valeur
propre de plus grand module n'est pas nulle, 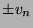 tend vers un vecteur
(normé) de cet espace propre.
tend vers un vecteur
(normé) de cet espace propre.
Démonstration :
si la base propre est  (avec
(avec
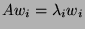 avec
avec
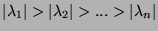 ) on a :
) on a :
donc :
et on pose
 .
Comme
.
Comme
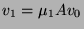 , on a :
, on a :
et on pose
 donc :
donc :
.....
si on pose
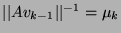 et
et
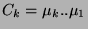 on a :
on a :
donc :
On a bien pour 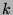 assez grand,
assez grand, 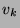 colinéaire au vecteur propre
colinéaire au vecteur propre 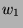 donc
donc
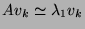 et puisque
et puisque 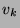 est de norme 1,
est de norme 1,
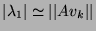 .
Si la première coordonnée
.
Si la première coordonnée 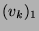 de
de 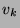 est non nulle, on a :
est non nulle, on a :
d'autre part :
donc 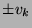 converge vers un vecteur propre, en pratique on teste
si
converge vers un vecteur propre, en pratique on teste
si
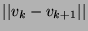 ou
ou
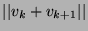 est inférieur à
est inférieur à 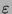 ,
auquel cas on arrête le calcul des
,
auquel cas on arrête le calcul des 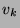 .
.
Exercice 3 (à rendre à la fin de la 2ème séance de ce TP)
Écrire un programme MuPAD ou calculatrice mettant en oeuvre
cet algorithme. Utilisez ce programme pour trouver une valeur approchée
de la valeur propre de norme maximale par la méthode
de la puissance de la matrice  de l'exercice 1 puis
d'une matrice aléatoire.
de l'exercice 1 puis
d'une matrice aléatoire.
Pour générer une matrice aléatoire:
- Avec
MuPAD utilisez linalg::randomMatrix(m, n,Dom::Integer)
- Avec maple utilisez linalg::randmatrix
- HP49:
RAND({4,4}), TI89/92: RandMat(4,4).
Attention, votre matrice aléatoire peut avoir un couple de complexe
conjugués comme valeur propre de plus grand module (en pratique
le test d'arrêt du programme ne sera jamais atteint). Dans ce cas
réessayez avec une autre matrice.



suivant: Méthode des itérations inverses.
monter: Méthode itératives
précédent: Méthode itératives
2003-02-19
![]() (avec
(avec
![]() avec
avec
![]() ) on a :
) on a :
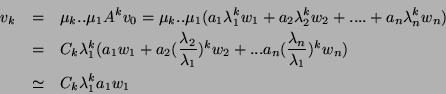
![]() de l'exercice 1 puis
d'une matrice aléatoire.
de l'exercice 1 puis
d'une matrice aléatoire.