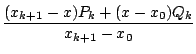


suivant: Intégration numérique
monter: Polynômes : arithmétique, factorisation, interpolation
précédent: Factorisation exacte
Index
Étant donné la facilité de manipulation qu'apportent les
polynomes, on peut chercher à approcher une fonction par un
polynôme. La méthode la plus naturelle consiste à chercher
un polynôme de degré le plus petit possible
égal à la fonction en certains points
x0,..., xn
et à trouver une majoration de la différence entre la fonction
et le polynôme.
Le polynome interpolateur de Lagrange répond à cette question.
Soit donc
x0,..., xn des réels distincts et
y0,..., yn
les valeurs de la fonction à approcher en ces points (on posera
yj = f (xj) pour approcher la fonction f). On cherche
donc P tel que
P(xj) = yi pour
j 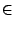 [0, n].
[0, n].
Commencons par voir s'il y a beaucoup de solutions. Soit P et Q
deux solutions distinctes du problème, alors P - Q est non nul
et va s'annuler en
x0,..., xn donc possède n + 1 racines donc
est de degré n + 1 au moins. Réciproquement, si on ajoute
à P un multiple du polynome
A = 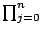 (X - xj), on obtient
une autre solution. Toutes les solutions se déduisent donc
d'une solution particulière en y ajoutant un polynome de degré
au moins n + 1 multiple de A.
(X - xj), on obtient
une autre solution. Toutes les solutions se déduisent donc
d'une solution particulière en y ajoutant un polynome de degré
au moins n + 1 multiple de A.
Nous allons maintenant construire
une solution particulière de degré au plus n.
Si n = 0, on prend P = x0 constant. On procède ensuite par
récurrence. Pour construire le polynôme correspondant
à
x0,..., xn+1 on part du polynoôme Pn correspondant à
x0,..., xn et on lui ajoute un multiple réel de A
Pn+1 =
Pn +
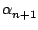
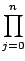
(
X -
xj)
Ainsi on a toujours
Pn+1(xj) = yj pour j = 0,..n, on calcule
maintenant
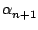 pour que
Pn+1(xn+1) = yn+1.
En remplacant avec l'expression de Pn+1 ci-dessus, on obtient
pour que
Pn+1(xn+1) = yn+1.
En remplacant avec l'expression de Pn+1 ci-dessus, on obtient
Pn(
xn+1) +
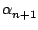
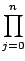
(
xn+1 -
xj) =
yn+1
Comme tous les xj sont distincts, il existe une solution unique :
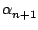
=
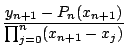
On a donc prouvé le :
Théorème 13
Soit n + 1 réels distincts
x0,..., xn et n + 1
réels quelconques
y0,..., yn.
Il existe un unique polynôme P de degré inférieur ou égal à
n, appelé polynome de Lagrange, tel que :
P(xi) = yi
Exemple : déterminons le polynome de degré inférieur ou égal
à 2 tel que
P(0) = 1, P(1) = 2, P(2) = 1. On commence par P0 = 1.
Puis on pose
P1 = P0 + 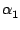 X = 1 +
X = 1 + 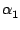 X.
Comme
P(1) = 2 = 1 +
X.
Comme
P(1) = 2 = 1 + 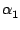 on en tire
on en tire
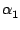 = 1
donc P1 = 1 + X. Puis on pose
P2 = P1 +
= 1
donc P1 = 1 + X. Puis on pose
P2 = P1 + 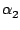 X(X - 1), on a
P2(2) = 3 + 2
X(X - 1), on a
P2(2) = 3 + 2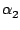 = 1
donc
= 1
donc
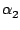 = - 1, finalement
P2 = 1 + X - X(X - 1).
= - 1, finalement
P2 = 1 + X - X(X - 1).
Reste à estimer l'écart entre une fonction et son polynome
interpolateur, on a le :
Ainsi l'erreur commise dépend d'une majoration de la taille
de la dérivée n + 1-ième sur l'intervalle, mais aussi
de la disposition des points xj par rapport à x. Par exemple
si les points xj sont équidistribués, le terme
|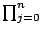 (x - xj)| sera plus grand près du bord de I qu'au
centre de I.
(x - xj)| sera plus grand près du bord de I qu'au
centre de I.
Preuve du théorème : Si x est l'un des xj l'égalité est vraie. Soit
C = (
f (
x) -
P(
x))/
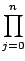
(
x -
xj)
on considère maintenant la fonction :
g(
t) =
f (
t) -
P(
t) -
C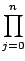
(
t -
xj)
elle s'annule en xj pour j variant de 0 à n ainsi qu'en x
suite au choix de la constante C, donc g s'annule au moins n + 2 fois
sur l'intervalle contenant les xj et x, donc g' s'annule au moins
n + 1 fois sur ce même intervalle, donc g'' s'annule au moins
n fois, etc. et finalement g[n+1] s'annule une fois
au moins sur cet intervalle. Or
g[n+1] = f[n+1] - C(n + 1)!
car P est de degré inférieur ou égal à n
et
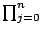 (x - xj) - xn+1 est de degré
inférieur ou égal à n. Donc il existe bien un réel
(x - xj) - xn+1 est de degré
inférieur ou égal à n. Donc il existe bien un réel 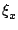 dans
l'intervalle contenant les xj et x tel que
dans
l'intervalle contenant les xj et x tel que
C =
![$\displaystyle {\frac{{f^{[n+1]}(\xi_x)}}{{(n+1)!}}}$](img164.png)
Calcul efficace du polynôme de Lagrange.
Avec la méthode de calcul précédent, on remarque que le
polynôme de Lagrange peut s'écrire à la Horner sous la forme :
| P(x) |
= |
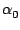 + + 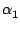 (x - x0) + ... + (x - x0) + ... + 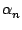 (x - x0)...(x - xn-1) (x - x0)...(x - xn-1) |
|
| |
= |
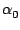 + (x - x0)( + (x - x0)(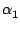 + (x - x1)( + (x - x1)(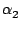 + ... + (x - xn-2)( + ... + (x - xn-2)(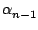 + (x - xn-1) + (x - xn-1)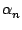 )...)) )...)) |
|
ce qui permet de le calculer rapidement une fois les 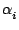 connus.
On observe que
On va voir que les
connus.
On observe que
On va voir que les 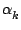 peuvent aussi se mettre sous forme
d'une différence.
On définit les différences divisées d'ordre n par récurrence
peuvent aussi se mettre sous forme
d'une différence.
On définit les différences divisées d'ordre n par récurrence
f[
xi] =
f (
xi),
f[
xi,...,
xk+i+1] =
![$\displaystyle {\frac{{f[x_{i+1},...,x_{k+i+1}]-f[x_i,...,x_{k+i}]}}{{x_{k+i+1}-x_i}}}$](img173.png)
On va montrer que
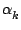 = f[x0,..., xk].
C'est vrai au rang 0, il suffit donc de le montrer au rang k + 1 en
l'admettant au rang k. Pour cela on observe qu'on peut construire
le polynôme d'interpolation en
x0,..., xk+1 à partir des polynômes
d'interpolation Pk en
x0,..., xk et Qk en
x1,..., xk+1
par la formule :
= f[x0,..., xk].
C'est vrai au rang 0, il suffit donc de le montrer au rang k + 1 en
l'admettant au rang k. Pour cela on observe qu'on peut construire
le polynôme d'interpolation en
x0,..., xk+1 à partir des polynômes
d'interpolation Pk en
x0,..., xk et Qk en
x1,..., xk+1
par la formule :
Pk+1(
x) =
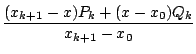
en effet on vérifie que
Pk+1(xi) = f (xi) pour
i 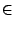 [1, k] car
Pk(xi) = f (xi) = Qk(xi),
et pour i = 0 et i = k + 1, on a aussi
Pk+1(x0) = f (x0) et
Pk+1(xk+1) = f (xk+1).
Or
[1, k] car
Pk(xi) = f (xi) = Qk(xi),
et pour i = 0 et i = k + 1, on a aussi
Pk+1(x0) = f (x0) et
Pk+1(xk+1) = f (xk+1).
Or
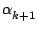 est le coefficient dominant de Pk+1 donc
c'est la différence du coefficient dominant de Qk et de Pk
divisée par
xk+1 - x0, c'est-à-dire la définition de
f[x0,..., xk+1] en fonction de
f[x1,..., xk+1] et
f[x0,..., xk].
est le coefficient dominant de Pk+1 donc
c'est la différence du coefficient dominant de Qk et de Pk
divisée par
xk+1 - x0, c'est-à-dire la définition de
f[x0,..., xk+1] en fonction de
f[x1,..., xk+1] et
f[x0,..., xk].
Exemple : on reprend
P(0) = 1, P(1) = 2, P(2) = 1. On a
| xi |
f[xi] |
f[xi, xi+1] |
f[x0, x1, x2] |
| 0 |
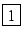 |
|
|
| |
|
(2 - 1)/(1 - 0) = 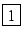 |
|
| 1 |
2 |
|
(- 1 - 1)/(2 - 0) = 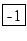 |
| |
|
(1 - 2)/(2 - 1) = - 1 |
|
| 2 |
1 |
|
|
donc
P(x) = 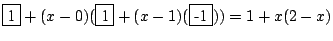 .
.
On peut naturellement utiliser l'ordre que l'on souhaite pour les
xi, en observant que le coefficient dominant de P ne dépend pas de
cet ordre, on en déduit que
f[x0,..., xk] est indépendant de
l'ordre des xi, on peut donc à partir du tableau ci-dessus
écrire P par exemple avec l'ordre 2,1,0, sous la forme
P(x) = 1 + (x - 2)(- 1 + (x - 1)(- 1)) = 1 + (x - 2)(- x)



suivant: Intégration numérique
monter: Polynômes : arithmétique, factorisation, interpolation
précédent: Factorisation exacte
Index
Retour à la page principale de mat249
![]() [0, n].
[0, n].
![]() (X - xj), on obtient
une autre solution. Toutes les solutions se déduisent donc
d'une solution particulière en y ajoutant un polynome de degré
au moins n + 1 multiple de A.
(X - xj), on obtient
une autre solution. Toutes les solutions se déduisent donc
d'une solution particulière en y ajoutant un polynome de degré
au moins n + 1 multiple de A.
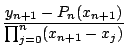
![]() X = 1 +
X = 1 + ![]() X.
Comme
P(1) = 2 = 1 +
X.
Comme
P(1) = 2 = 1 + ![]() on en tire
on en tire
![]() = 1
donc P1 = 1 + X. Puis on pose
P2 = P1 +
= 1
donc P1 = 1 + X. Puis on pose
P2 = P1 + ![]() X(X - 1), on a
P2(2) = 3 + 2
X(X - 1), on a
P2(2) = 3 + 2![]() = 1
donc
= 1
donc
![]() = - 1, finalement
P2 = 1 + X - X(X - 1).
= - 1, finalement
P2 = 1 + X - X(X - 1).
![$\displaystyle {\frac{{f^{[n+1]}(\xi_x)}}{{(n+1)!}}}$](img164.png)
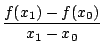
![$\displaystyle {\frac{{f[x_{i+1},...,x_{k+i+1}]-f[x_i,...,x_{k+i}]}}{{x_{k+i+1}-x_i}}}$](img173.png)