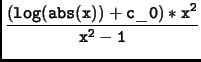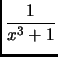Exercices utilisant différentes commandes

1. Calculer
   $$\int_{1}^{2}$$$${\frac{1}{x^3+1}}$$dx
   On tape :
   $$\tt int(1/(x\circonflexe3+1),x,1,2)$$
   On obtient apres simplification (en utilisant normal :
   $$\tt (sqrt(3)*log(2)+pi)*1/3/sqrt(3)$$

2. Soit M_a = $\left[\vphantom{ \begin{array}{ccc} 2a-1 & a & 2a-1\\ a^2+a-2 & a^2-1 & a-1\\ a^2+a-1 & a^2+a-1 & a \end{array}}\right.$$\begin{array}{ccc} 2a-1 & a & 2a-1\\ a^2+a-2 & a^2-1 & a-1\\ a^2+a-1 & a^2+a-1 & a \end{array}$$\left.\vphantom{ \begin{array}{ccc} 2a-1 & a & 2a-1\\ a^2+a-2 & a^2-1 & a-1\\ a^2+a-1 & a^2+a-1 & a \end{array}}\right]$
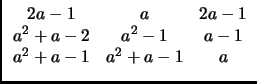
   a) Pour quelles valeurs de a, M_a est-elle inversible ?
   Préciser son rang lorsqu'elle n'est pas inversible.
   b) Calculer l'inverse deM₂

   On tape :

   $$\tt M:=[[2a-1,a,2a-1],[a^2+a-2,a^2-1,a-1],[a^2+a-1,a^2+a-1,a]]$$
   ou on se sert de l'éditeur de matrices pour entrer la matrice.
   On calcule le déterminant de M, on tape :
   $$\tt det(M)$$
   On obtient :
   $$\tt 2*a^4+-2*a^3+-2*a^2+2*a$$
   Pour avoir l'inverse de M on tape :
   $$\tt inv(M)$$
   On obtient dans l'historique :
   $$\tt\frac{1}{2a^4-2a^3-2a^2+2a}\left[ \begin{array}{ccc} a-1 & 2a... ...2+2a-1 & 2a^3-a^2-2a+1\\ a^3-2a+1 & -a^3+2a-1 & a^3-2a^2+1 \end{array}\right]$$
   On tape :
   $$\tt solve(2a^4-2*a^3-2*a^2+2*a,a)$$
   On obtient :
   $$\tt [-1,0,1]$$
   Donc la matrice est inversible si a $\not\in$[- 1, 0, 1] Ou on tape :
   $$\tt factor(2a^4-2*a^3-2*a^2+2*a)$$
   On obtient :
   $$\tt 2*(a+1)*a*(a-1)^2$$
   On tape :
   $$\tt rank(subst(M,a,-1))$$
   On obtient :
   $$\tt 2$$
   On tape :
   $$\tt rank(subst(M,a,0))$$
   On obtient :
   $$\tt 2$$
   On tape :
   $$\tt rank(subst(M,a,1))$$
   On obtient :
   $$\tt 1$$
   On tape :
   $$\tt inv(subst(M,a,2))$$
   On obtient : A = ${\frac{1}{12}}$$\left[\vphantom{ \begin{array}{ccc} 1 & 11 & -7\\ -3 & -9 & 9\\ 5 & -5 & 1 \end{array}}\right.$$\begin{array}{ccc} 1 & 11 & -7\\ -3 & -9 & 9\\ 5 & -5 & 1 \end{array}$$\left.\vphantom{ \begin{array}{ccc} 1 & 11 & -7\\ -3 & -9 & 9\\ 5 & -5 & 1 \end{array}}\right]$
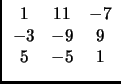
   Remarque : pour éviter de faire des substitutions on peut définir la matrice M comme une fonction de a, il faut alors écrire :
   $\tt M(a):=\{[[2a-1,a,2a-1],[a^2+a-2,a^2-1,a-1],[a^2+a-1,a^2+a-1,a]]\}$
   surtout ne pas oublier { et } car M(a) : = [..] serait considéré comme étant la définition d'un programme.
   On peut alors taper : inv(M(2).
3. Soit A = $\left[\vphantom{ \begin{array}{ccc} 1 & 1 & a\\ 1 & a & 1\\ a & 1 & 1 \end{array}}\right.$$\begin{array}{ccc} 1 & 1 & a\\ 1 & a & 1\\ a & 1 & 1 \end{array}$$\left.\vphantom{ \begin{array}{ccc} 1 & 1 & a\\ 1 & a & 1\\ a & 1 & 1 \end{array}}\right]$
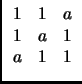
   Pour quelles valeurs de a, A est-elle diagonalisable ?

   On tape :

   $$\tt A:=[[1,1,a],[1,a,1],[a,1,1]]$$
   ou on se sert de l'éditeur de matrices pour entrer la matrice :
   Pour avoir les valeurs propres de A on tape :
   $$\tt egvl(A)$$
   On obtient dans l'historique :
   $$\tt\left[ \begin{array}{ccc} -a+1 & 0 & 0\\ 0 & a+2 & 0\\ 0 & 0 & a-1 \end{array}\right]$$
   ce qui s'écrit dans la ligne de commande : $\tt [[-a+1,0,0],[0,a+2,0],[0,0,a-1]]$
   Si a $\neq$ 1 il y a 3 valeurs propres distinctes - a + 1, a + 2, a - 1 et
   si a = 1 il y a une valeur propre double ($\lambda$ = 0) et une valeur propre simple ($\lambda$ = 3).
   Puis on cherche la matrice de passage, on tape :
   $$\tt egv(A)$$
   On obtient dans l'historique :
   $$\tt\left[ \begin{array}{rrr} -1 & 1 & 1\\ 0 & 1 & -2\\ -1 & 1 & 1 \end{array}\right]$$
   ce qui s'écrit dans la ligne de commande :
   
   $$\tt [[1,1,1],[0,1,-2],[-1,1,1]]$$
   les vecteurs propres sont les colonnes de cette matrice.
   Ou on tape pour avoir directement les deux informations, matrice de passage et réduite de Jordan :
   $$\tt jordan(A)$$
   On obtient dans l'historique une liste de deux matrices [P, B] (P est la matrice de passage et B = P^-1AP) :
   $$\tt\left[ \left[ \begin{array}{rrr} -1 & 1 & 1\\ 0 & 1 & -2\\ ... ...}{ccc} -a+1 & 0 & 0\\ 0 & a+2 & 0\\ 0 & 0 & a-1 \end{array}\right] \right]$$
   ce qui s'écrit dans la ligne de commande :
   
   $$\tt [[[1,1,1],[0,1,-2],[-1,1,1]],[[-a+1,0,0],[0,a+2,0],[0,0,a-1]]]$$
   On remarque qu'en faisant : $\tt a:=1$ puis $\tt jordan(A)$
   les valeurs propres doubles sont regroupées et on obtient :
   $$\tt\left[ \left[ \begin{array}{rrr} 1 & -3 & 0\\ 1 & 0 & -3\\ ... ...n{array}{ccc} 3 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right] \right]$$
   :
   ce qui s'écrit dans la ligne de commande :
   $\tt [[[1,-3,0],[1,0,-3],[1,3,3]],[[3,0,0],[0,0,0],[0,0,0]]]$
   A est donc diagonalisable quelque soit a et B = P^-1AP.
4. Donner un développement limité à l'ordre 7 au voisinage de x = 0 de :
   sin(sinh(x)) - sinh(sin(x))
   On tape :
   $$\tt series(sin(sinh(x))-sinh(sin(x)),x=0,7)$$
   On obtient:
   $$\tt 1/-45*x^7+x^8*order\_size(x)$$
   La fonction $\tt order\_size$ est telle que, pour tout $\tt\alpha>0$, $\tt x^\alpha order\_size(x)$ tend vers 0 quand $\tt x$ tend vers 0.
5. Donner un développement limité à l'ordre 4 au voisinage de x = 0 de :
   $${\frac{\ln(\cos(x))}{\exp(x+x^2)}}$$
   On tape :
   $$\tt series(\ln(\cos(x))/\exp(x+x^2),x=0,4)$$
   On obtient :
   $$\tt 1/-2*x^2+1/2*x^3+1/6*x^4+x^5*order\_size(x)$$
   La fonction $\tt order\_size$ est telle que, pour tout $\tt\alpha>0$, $\tt x^\alpha order\_size(x)$ tend vers 0 quand $\tt x$ tend vers 0.
6. Trouver les solutions de l'équation différentielle :
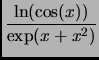
   x(x² - 1)y' + 2y = 0
   On tape :
   $$\tt desolve(x*(x^2-1)*y'+2*y=0,y)$$
   On obtient :
   $$\tt\frac{c\_0*x^2}{x^2-1}$$

7. Trouver les solutions de l'équation différentielle :
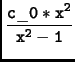
   x(x² - 1)y' + 2y = x²
   On tape :
   $$\tt desolve(x*(x^2-1)*y'+2*y=x^2,y)$$
   On obtient :
   $$\tt\frac{(log(abs(x))+c\_0)*x^2}{x^2-1}$$