Chapitre 6  Probabilités et simulation

6.1  Rappels : les fonctions aléatoires de Xcas

6.1.1  Pour initialiser les nombres aléatoires : srand randseed RandSeed

srand() (ou randseed ou RandSeed) sert à initialiser la suite des nommbres aléatoires que l’on obtient avec rand() ou avec randnorm().
RandSeed a toujours un argument entier, alors que randseed ou srand peut ne pas avoir d’arguments (dans ce cas le générateur aléatoire est intialisé avec l’horloge du système).
On tape :

On obtient par exemple :

Ou on tape :

On obtient par exemple :

Ou on tape :

On obtient par exemple :

6.1.2  Tirage équiréparti rand alea hasard

Tirage équiréparti sur [0,1,..,2³²[ : rand() alea() hasard()

rand() renvoie au hasard, de façon équiprobable, un nombre entier de [0,2³²[ (2³²=4294967296).
On tape :

ou on tape

On obtient :

Pour avoir, au hasard, de façon équiprobable, un nombre de [0;1[, on peut donc utiliser :

On obtient :

Mais il est plus simple de taper : rand(0,1) (voir le paragraphe suivant).

Tirage aléatoire équiréparti sur l’intervalle [a;b[ : rand(a,b) hasard(a,b) rand(a..b)() hasard(a..b)()

Si a et b sont des réels rand(a,b) désigne un nombre décimal aléatoire compris dans l’intervalle [a;b[.
Donc, rand(a,b) ou (hasard(a,b)) renvoie au hasard, et de façon équiprobable, un nombre décimal de [a;b[.
Pour avoir, au hasard et de façon équiprobable, un nombre décimal de [0;1[, on tape :

On obtient :

Pour avoir, au hasard et de façon équiprobable, un nombre décimal de [0;0.5[, on tape :

On obtient :

Pour avoir, au hasard et de façon équiprobable, un nombre décimal de ]−0.5;0], on tape :

ou on tape :

On obtient par exemple :

Si a et b sont des réels rand(a..b) ou alea(a..b) ou hasard(a..b) désigne une fonction qui est un générateur de nombres aléatoires compris dans l’intervalle [a;b[.
Donc, rand(a..b)() renvoie au hasard, et de façon équiprobable, un nombre décimal de [a;b[.
Pour avoir, au hasard et de façon équiprobable, un nombre décimal de [0;1[, on tape :

On obtient :

Pour avoir, au hasard et de façon équiprobable, plusieurs nombres aléatoires décimaux compris dans l’intervalle [1;2[, on tape :

puis il suffit de taper r().
On tape :

On obtient :

Tirage aléatoire d’entiers équirépartis sur [0,..,n[ : rand(n) alea(n) hasard(n)

Si n est un entier relatif rand(n) ou hasard(n) renvoie au hasard, et de façon équiprobable, un entier de [0,1,..,n[ (ou de ]n,..1,0] si n est negatif).
On tape :

Ou on tape :

On obtient :

ou on obtient :

On tape :

Ou on tape :

On obtient :

ou on obtient :

On tape pour avoir un entier aléatoire entre 6 et 10, bornes comprises :

Ou on tape :

On obtient par exemple :

6.1.3  Tirage aléatoire sans remise de p objets parmi n : rand alea hasard

rand a dans ce cas, soit 2, soit 3 arguments.
Si rand a 2 arguments : les arguments sont un entier p et une liste L alors rand(p,L) renvoie, au hasard, p éléments de la liste L.
Si rand a 3 arguments : les arguments sont trois entiers p,min,max alors rand(p,min,max) renvoie, au hasard, p entiers de [min,..,max] On tape :

On obtient :

On tape :

On obtient :

On tape :

On obtient :

6.1.4  Tirage aléatoire selon la loi binomiale négative

6.1.5  Tirage aléatoire avec remise de n objets parmi k

Choisir au hasard n nombres selon la loi multinomiale de probabilité P. Cela veut dire qu’on effectue un tirage avec remise de n objets parmi k=size(P) objets. Pour j=0..k-1, l’objet j a la probabilité P[j] dêtre tiré (on doit avoir pour sum(P)=1). On tape :

randmult(n,P):={
  local k,j,l,r,X,L;
  k:=size(P);
  X:=cumsum(P);
  si X[k-1]!=1 alors return "erreur"; fsi;
    L:=[0$(j=1..k)];
  pour j de 1 jusque n faire 
    r:=alea(0,1);
    //afficher(r);
    l:=0;
    tantque r>X[l] faire
      l:=l+1;
    ftantque;
  L[l]:=L[l]+1  
  fpour;
  return L;
}:;

On tape :
randmult(5,[1/2,1/3,1/6])
On obtient par exemple :
[3,1,0]
ou bien, on utilise la commande Xcas : randvector avec multinomial comme paramètre On tape :
randvector(5,multinomial,[1/2,1/3,1/6])
On obtient par exemple :
[3,1,1]
Si on effectue un tirage avec remise de n objets de la liste C. Si k=size(C), l’objet C[j] a la probabilité P[j] dêtre tiré pour (j=0..k-1). On doit avoir k=size(C)=size(P) et sum(P)=1.
Si n==1, on renvoie l’objet qui a été tiré.
Si n!=1, on renvoie la séquence de k listes constituées du nom des objets et de leur nombre d’apparition.
On tape :

randmultinom(n,P,C):={
  local k,j,l,r,X,L;
  k:=size(P);
  si size(C)!=k alors retourne "erreur"; fsi;
  X:=cumsum(P);
  si X[k-1]!=1 alors return "erreur"; fsi;  
    L:=[C[j],0]$(j=0..k-1);
  pour j de 1 jusque n faire 
    r:=alea(0,1);
    l:=0;
    tantque r>X[l] faire
      l:=l+1;
    ftantque;
  L[l,1]:=L[l,1]+1  
  fpour;
  si n==1 alors return L[l,0];fsi;
 return L; 
}:;

On tape :
randmultinom(5,[1/2,1/3,1/6],["R","V","B"])
On obtient par exemple :
[["R",2],["V",2],["B",1]]
ou bien, on utilise la commande Xcas : randvector avec multinomial comme paramètre On tape :
randvector(5,multinomial,[1/2,1/3,1/6],["R","V","B"])
On obtient dans ce cas la liste des 5 tirages, par exemple :
["R","B","R","R","V"]
On simule le tirage de 1 objet parmi 3 objets de probabilité respective :
P=[1/2,1/3,1/6] en faisant 6000 tirages.
On tape :
randmult(6000,[1/2,1/3,1/6])
On obtient par exemple :
[3026,2009,965]
ou bien, on utilise la commande Xcas : randvector avec multinomial comme paramètre On tape :
randvector(6000,multinomial,[1/2,1/3,1/6])
On obtient, par exemple :
[2947,2040,1013]
On écrit le programme qui simule m fois le choix au hasard de n nombres selon la loi multinomiale de probabilité P et qui compte le nombre r de fois que l’on a obtenu le tirage K (sum(K)=n) et qui renvoie r/m c’est à dire une estimation de la probabilité d’obtenir K. probmult(m,n,P,K) renvoie donc ne estimation de multinomiale(n,P,K). On tape :

probmult(m,n,P,K):={
  local l,T,r;
  r:=0;
  pour l de 1 jusque m faire
    T:=randmult(n,P);
    si T==K alors r:=r+1; fsi;
  fpour;
return r/m;
}:;

Exercice Soit une urne ayant 3 boules noires, 2 boules rouges et 1 boule verte. On tire avec remise 2 boules de cette urne.
Quelle est la probabilité de tirer une boule rouge et une boule verte ?
On peut simuler le tirage avec remise 2 boules de cette urne avec :
randmult(2,[1/2,1/3,1/6])
qui renvoie par exemple :
[1,0,1]
randmultinom(2,["N","R","V"],[1/2,1/3,1/6])
qui renvoie par exemple :
[["N",1],["R",0],["V",1]]
On simule 6000 fois ce tirage et on tape :
probmult(6000,2,[1/2,1/3,1/6],[0,1,1])
On obtient par exemple :
671/6000
671/6000. ≃ 0.111833333333 On utilise la commande multinomial de Xcasé et on tape : multinomial(2,[1/2,1/3,1/6],[0,1,1])
On obtient :
1/9
1/9. ≃ 0.111111111111
Exercice Une urne contient 12 boules rouges et 3 boules vertes. On se propose de simuler le tirage d’une boule de l’urne puis d’observer la fluctuation d’échantillonnage sur des échantillons de taille 225. D’après le contenu de l’urne, la probabilité de tirer une boule verte est de 1/5=0.2.
Notre simulation est-elle convenable ? On tape :
L:=[randmultinomial([4/5,1/5],["R","V"])$(j=1..225)]:;
On obtient :
Done
On tape :
count_eq("V",L)
On obtient par exemple :
45
On analyse tout d’abord 50 échantillons de taille 225 pour voir la fluctuation.
On note N le nombre de fois que l’on fait une simulation (une simulation c’est 225 tirages).
n le nombre de fois que l’on a obtenu une boule verte,
p le pourcentage de boules vertes obtenues par cette simulation,
Lp la séquence des pourcentages obtenues.
On tape :

test0(N):={
  local L,p,n,k,Lp;
  Lp:=NULL;
pour k de 1 jusque N faire
  L:=[randmultinomial([4/5,1/5],["R","V"])$(j=1..225)];
  n:=count_eq("V",L)
  p:=n/225.;
  Lp:=Lp,p;
fpour;
 retourne Lp;
  }:;

Puis :
plotlist(test0(50)),droite(y=2/15),droite(y=4/15)
On obtient :
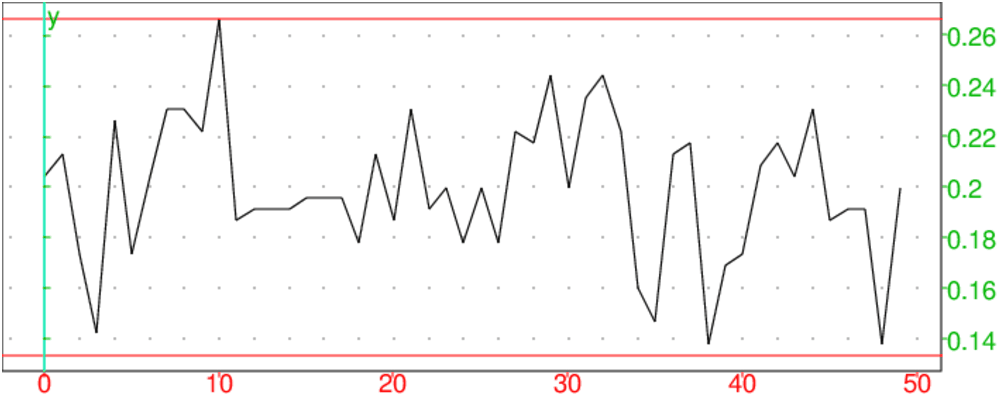On analyse successivement t échantillons de taille n=225 pour, t∈ 10, 20, 50, 100, 200, 500. Pour notre problème, l’intervalle de fluctuation au seuil de 95% est : p−1/√n p+1/√n avec p=1/5 et n=225 c’est à dire 2/15,4/15
Pour savoir si la simulation est corecte on fait un programme pour savoir si on a bien dans 95% des cas p dans l’intervalle 2/15,4/15
On note N le nombre de fois que l’on fait une simulation (une simulation c’est 225 tirages).
Pour la k ième simulation, (k=1..N) on note :
L la liste des 225 tirages obtenus,
n le nombre de fois que l’on a obtenu une boule verte,
p le pourcentage de boules vertes obtenues par cette simulation,
l s le nombre de tirages tels que 2/15<p<4/15 lorsqu’on a fait k simulations,
sn le nombre de fois que l’on a obtenu une boule verte lorsqu’on a fait k simulations.
pcn le pourcentage de boules vertes obtenues par ces N*225 tirages est donc sn/(225*N) Le nombre de fois où on a 2/15<p<4/15 est s. En pourcentage cela fait donc pc=s/N.
On vérifie alors si pc>0.95

test0(N):={
  local s,L,p,n,pc,sn,pcn,k,Le;
  s:=0;sn:=0;
Le:=NULL;
pour k de 1 jusque N faire
  L:=[randmultinomial([4/5,1/5],["R","V"])$(j=1..225)];
  n:=count_eq("V",L)
  p:=n/225;
  Le:=Le,p;
fpour;
 retourne Le;
  }:;
test(N):={
  local s,L,p,n,pc,sn,pcn,k,Le;
  s:=0;sn:=0;
Le:=NULL;
pour k de 1 jusque N faire
  L:=[randmultinomial([4/5,1/5],["R","V"])$(j=1..225)];
  n:=count_eq("V",L)
  p:=n/225;
  Le:=Le,p;
  si p>2/15 and p<4/15 alors s:=s+1; fsi;
  sn:=sn+n;
fpour;
  pc:=evalf(s/N);
  pcn:=evalf(sn/N/225);
  si pc>0.95 alors retourne pcn,pc,"correcte"; sinon retourne pcn,pc,"pas correcte"; fsi;
  }:;

On tape :
test(10)
On obtient :
0.203111111111,1.0,"correcte"
On tape :
test(20)
On obtient :
0.194888888889,0.95,"pas correcte"
On tape :
test(50)
On obtient :
0.194311111111,0.98,"correcte"
On tape :
test(100)
On obtient :
0.198888888889,0.97,"correcte"
On tape :
test(200)
On obtient :
0.193777777778,0.99,"correcte"
test(500)
On obtient :
0.19984,0.984,"correcte"
On tape :
plotlist([10,20,50,100,200,500],[0.203,0.195,0.194,0.199,0.1940.1999] ), droite(y=0.2)
On obtient :

6.1.6  Tirage selon une loi normale : randnorm randNorm

randnorm(m,sigma) ou randNorm(m,sigma) renvoie au hasard des nombres répartis selon la loi normale de moyenne m et d’écart type sigma.
On tape :

On obtient par exemple :

ou on obtient par exemple :

On tape :

On obtient par exemple :

6.1.7  Tirage selon une loi exponentielle : randexp

randexp(a) renvoie au hasard des nombres répartis selon la loi exponentielle de paramètre a positif.
La densité de probabilité est proportionnelle à exp(−a*t) et on a :
Proba(X≤ t)=a∫₀^texp(−a*u)du.
On tape :

On obtient par exemple :

ou on obtient par exemple :

6.1.8  Matrice aléatoire : ranm randmatrix randMat

ranm (ou randmatrix ou randMat) peut avoir comme 1,2 ou 3 arguments :

• avec un entier s comme argument, ranm renvoie une liste de longueur s dont les éléments sont des entiers pris au hasard de façon équiprobable dans :
  [-99,-98,...,98,99].
  On tape :
  ranm(5)
  On obtient par exemple :
  [-40,27,4,-1,94]
• avec deux entiers n,p comme argument, ranm renvoie une matrice de n lignes et p colonnes dont les éléments sont des entiers pris au hasard de façon équiprobable dans :
  [-99,-98,...,98,99].
  On tape :
  ranm(2,3)
  On obtient par exemple :
  [[-32,53,-44],[10,-4,25]]
• avec deux entiers n,p et un entier relatif a comme argument, ranm renvoie une matrice de n lignes et p colonnes dont les éléments sont des entiers pris au hasard de façon équiprobable dans [0;a[ (ou ]a;0] si a est négatif)
  On tape :
  ranm(2,3,10)
  On obtient par exemple :
  [[8,3,7],[7,9,1]]
• avec deux entiers n,p et un intervalle a..b comme argument, ranm renvoie une matrice de n lignes et p colonnes dont les éléments sont des réels pris au hasard de façon équiprobable dans [a;b[.
  On tape :
  ranm(2,3,0..1)
  On obtient par exemple :
  [[0.840187716763,0.394382926635,0.783099223394],
  [0.798440033104,0.911647357512,0.197551369201]]
• deux entiers n,p et une fonction aléatoire de Xcas qu’il faut quoter, dans ce cas ranm renvoie une matrice de n lignes et p colonnes dont les éléments sont pris au hasard selon la fonction donnée en troisième argument.
  On tape :
  ranm(3,2,’rand(3)’)
  ou
  ranm(3,2,3)
  On obtient par exemple :
  [[2,1],[0,0],[1,0]]
  On tape :
  ranm(1,2,’randnorm(0,1)’)
  On obtient par exemple :
  [[1.37439065645,-1.33195982697]]

6.2  Déplacement aléatoire

6.2.1  Déplacement sur un axe

Une tortue se déplace sur un axe gradué.
Au début de chaque parcours la tortue se trouve à l’origine.
On choisit de la faire avancer en jouant à pile ou face : pile la tortue reste sur place, face elle avance d’une unité.
Un parcours aléatoire de la tortue est constitué par 5 tirages aléatoires.
On veut simuler 30 parcours aléatoires et trouver la probabilité de l’événement : la tortue est arrivée au point d’abscisse x_i pour x_i ∈ ℕ.

Simulation d’un parcours

On note T l’abscisse du point d’arrivée de la tortue.
On écrit le programme parcours, en utilisant rand(2) qui renvoie de façon équiprobable 0 ou 1.
On considère que 0 correspond à pile et correspond 1 à face.

parcours() :={
  local T,r;
  T:=0;
  // on fait 5 tirages
  for (k:=1;k<6;k++){ 
    r:=rand(2);
    // la tortue avance si r==1 (tirage = face)
    if (r==1){
       T:=T+1;
    }
  }
  return(T);
}; 

Voici les résultats obtenus lorsque l’on fait 10 fois parcours() ,on tape:
for (k:=1;k<11;k++) parcours()
On obtient par exemple :
4,2,4,1,1,4,3,2,2,1

Simulation de n parcours

On note T l’abscisse du point d’arrivée de la tortue et TA le tableau des résultats : TA[0] represente le nombre de fois que la tortue est au point 0 à l’arrivée.
On écrit le programme suivant dans l’éditeur de programmes de Xcas (raccourci Alt+p) et on sauve ce programme dans le fichier parsim.

parcoursim(n) :={
  local T,r,TA,R,j,k;
  ClrGraph();
  TA:=[0,0,0,0,0,0];
  for (j:=1;j<n+1;j++){
    T:=0;
    for (k:=1;k<6;k++){ 
      r:=rand(2);
      if (r==1){
        T:=T+1;
      }
    }
  TA[T]:=TA[T]+1;
  };
  orint(TA);
  switch_axes(NULL);
  xyztrange(-0.5,5.2,-0.1,16.0,-10.0,10.0,-10.0,-10.0,
            -0.5,5.2,-0.1,16.0,1);
  R:=segment(0,i*TA[0]); 
  R:=R,segment(1,1+i*TA[1]);
  R:=R,segment(2,2+i*TA[2]);
  R:=R,segment(3,3+i*TA[3]);
  R:=R,segment(4,4+i*TA[4]);
  R:=R,segment(5,5+i*TA[5]);
  return R;
}; 

Attention Ici parcoursim renvoie une liste de segments et écrit en bleu la valeur de TA. Le programme se trouve dans un éditeur prg de Xcas, on le teste avec le bouton OK, puis si on a obtenu //Success compilling, le programme est validé.
On tape dans la ligne de commande :
parcoursim(30)
On obtient en bleu :
TA:[0,4,14,6,6,0]
et le graphique :

Voici des résultats obtenus pour la liste des abscisses des points d’arrivée :
pour parcoursim(30) on a trouvé [0,2,7,13,7,1]
pour parcoursim(300) on a trouvé [7,41,94,102,47,9]
pour parcoursim(1000) on a trouvé [36,172,310,306,148,28]
pour parcoursim(10000) on a trouvé [287,1575,3184,3136,1517,301]

Analyse des résultats

Soit l’univers Ω formé par les 5 tirages successifs possibles (chacun étant équiprobable) :
Ω={{p,p,p,p,p},{p,p,p,p,f},{p,p,p,f,p},...,{f,f,f,f,f,}}.
Ω a 2⁵=32 éléments.
Soit A la variable aléatoire égale à l’abscisse du point d’arrivée.
On a :
P(A=0)=1/2⁵=0.03125 car cela correspond à 5 fois "pile",
P(A=1)=5/2⁵=0.15625 car cela correspond à 4 fois "pile" et 1 fois "face" ce qui peut se produire de 5 façons,
P(A=2)=10/2⁵= 0.3125 car cela correspond à 3 fois "pile" et 2 fois "face" ce qui peut se produire de C₅²= 10 façons,
P(A=3)=10/2⁵= 0.3125 car cela correspond à 2 fois "pile" et 3 fois "face" ce qui peut se produire de C₅³= 10 façons,
P(A=4)=5/2⁵=0.15625 car cela correspond à 1 fois "pile" et 4 fois "face" ce qui peut se produire de 5 façons,
P(A=5)=1/2⁵=0.03125 car cela correspond à 5 fois "face".

6.2.2  Déplacement dans deux directions

Au début de chaque parcours la tortue se trouve à l’origine.
On choisit de la faire avancer en jouant à pile ou face :
- pile, la tortue avance d’une unité selon un axe vertical,
- face, elle avance d’une unité selon un axe horizontal.
Un parcours aléatoire de la tortue est constitué par 5 tirages aléatoires.
On veut simuler n parcours aléatoires et trouver la probabilité de l’évènement : le parcours aléatoire de la tortue se termine au point de coordonnées [x,y] pour (x,y) ∈ N × N

Simulation d’un parcours

On note X,Y les coordonnées du point d’arrivée de la tortue.
On écrit :

parcours2() :={
  local X,Y,r;
  X:=0;
  Y:=0;
  for (k:=1;k<6;k++){
    r:=rand(2);
    if (r==1){
       X:=X+1;
    } else {
       Y:=Y+1;
    }
  }
  return([X,Y]);
}; 

Voici les résultats obtenus lorsque l’on fait 10 fois parcours2() :
[2,3],[1,4],[3,2],[4,1],[3,2],[2,3],[1,4],
[1,4],[3,2],[2,3]
On remarque qu’à chaque tirage soit X, soit Y est augmenté d’une unité donc à chaque tirage X+Y aygmente de 1. Au début X+Y=0, donc, au bout de 5 tirages c’est à dire à la dernière étape X+Y=5.
Il suffit donc de connaitre l’abscisse d’arrivée X pour connaitre le point d’arrivée (point(X,5-X))). Ce problème est donc le même que le précédent.

Simulation de n parcours

On note XA le tableau des résultats selon les abscisses.
On remarquera qu’ici Y ne sert à rien puisqu’on peut repérer le point d’arrivée seulement à l’aide de son abscisse, elle permet juste de visualiser le point d’arrivée.
On écrit :

parcoursim2(n) :={
  local X,Y,r,j,k,XA;
  XA:=[0,0,0,0,0,0];
  for (j:=1;j<n+1;j++){
    r:=rand(2);
    X:=0;
    Y:=0;
    for (k:=1;k<6;k++){
      if (r==1){
        X:=X+1;
      } else {
        Y:=Y+1;
      }
    r:=rand(2);
    }
  XA[X]:=XA[X]+1;
  }
  switch_axes(NULL);
  ClrGraph();
  xyztrange(-0.5,5.2,-0.1,16.0,-10.0,10.0,-10.0,-10.0,
            -0.5,5.2,-0.1,16.0,1);
 
  return([XA,segment(0,i*XA[0]),segment(1,1+i*XA[1]),
     segment(2,2+i*XA[2]),segment(3,3+i*XA[3]),
     segment(4,4+i*XA[4]),segment(5,5+i*XA[5])]);
}; 

Voici les résultats obtenus :
pour parcoursim2(30) on a trouvé :
XA=[0,4,9,9,7,1]
pour parcoursim2(300) on a trouvé :
XA=[6,48,91,99,46,10]
pour parcoursim2(1000) on a trouvé :
XA=[26,170,313,320,148,23]
pour parcoursim2(10000) on a trouvé :
XA=[290,1498,3207,3128,1572,305]
Attention Ici parcoursim2 renvoie une liste de segments : ces segments seront donc dessinés dans un écran de géométrie et dans l’écran DispG. Il faut donc écrire ClrGraph() en début de programme si on veut effacer l’écran de géométrie DispG.

Analyse des résultats

On a donc la même analyse que dans le parcours linéaire.
Soit A la variable aléatoire égale aux coordonnées du point d’arrivée.
P(A=[0,5])=1/2⁵= 0.03125 car cela correspond à 5 fois "pile",
P(A=[1,4])=5/2⁵=0.15625 car cela correspond à 4 fois "pile" et 1 fois "face" ce qui peut se produire de 5 façons,
P(A=[2,3])=10/2⁵=0.3125 car cela correspond à 3 fois "pile" et 2 fois "face" ce qui peut se produire de C₅²= 10 façons,
P(A=[3,2])=10/2⁵= 0.3125 car cela correspond à 2 fois "pile" et 3 fois "face" ce qui peut se produire de C₅³= 10 façons,
P(A=[4,1])=5/2⁵=0.15625 car cela correspond à 1 fois "pile" et 4 fois "face" ce qui peut se produire de 5 façons,
P(A=[5,0])=1/2⁵= 0.03125 car cela correspond à 5 fois "face".

6.3  Les trois cartes bicolores

On met dans un chapeau trois cartes : une des cartes a deux côtés rouges, une autre a un côté rouge et un côté blanc et la troisième a deux côtés blancs.
On tire une carte : le côté que nous voyons est rouge.
Quelle est la probabilité pour que l’autre côté soit blanc ?

6.3.1  Simulation de n tirages

Pour écrire le programme de simulation, on numérote les cartes par 0,1 et 2 et on numérote les faces de chaque carte par 0 et 1 : par exemple la carte blanche a le numéro 0, la carte bicolore a le numéro 1, la carte rouge a le numéro 2 et la face blanche de la carte bicolore a le numéro 0.
Puis, on représente donc une carte par un vecteur qui est la couleur de ses faces :
par exemple la carte bicolore sera représentée par [B,R].
On peut aussi représenter le blanc par 0 et le rouge par 1 :
par exemple la carte bicolore sera représentée par [0,1].
On représente ainsi les cartes par un vecteur de deux composantes 0 ou 1 (0 et 1 désigne la couleur).
La variable C:=[[0,0],[0,1],[1,1]] représente donc les trois cartes :
[0,0] est la carte avec 2 faces blanches, [1,1] est la carte avec 2 faces rouges et [0,1] est la carte bicolore (on a supposé que la face blanche a le numéro 0 et la rouge le numéro 1).
C est donc une matrice et la valeur de C[a,b] (pour a=0,1,2 et b=0,1) représente la couleur de la face b de la carte a.
On tire une des cartes (a:=rand(3);),
puis on tire la face visible (b:=rand(2);).
Si b est la face visible, irem(b+1,2) c’est à dire b+1 mod 2 est la face cachée.
On simule n tirages qui donne comme coté visible une face rouge et on compte le nombre de cartes bicolores.
On écrit pour cela le programme cartebicolor :

cartebicolor(n):={
local C,a,b,nbi;
C:=[[0,0],[0,1],[1,1]];
//nbi est le nbre de cartes bicolores obtenus 
//qd la face visible est blanche
nbi:=0
for (k:=0;k<n;k++){
//on tire une carte
a:=rand(3);
// on tire une face (la face visible)
b:=rand(2);
// on refait le tirage si la face visible est blanche
while (C[a,b]==0) {
a:=rand(3);
b:=rand(2);
}
//la face visible est rouge, si la face cachee est blanche,
// nbi augmente de 1
if (C[a,irem(b+1, 2)]]==0) {
nbi:=nbi+1;
}
}
return(evalf(nbi/n));
};

On a obtenu :
cartebicolor(300)=0.34
cartebicolor(3000)=0.343666666667
cartebicolor(30000)=0.331533333333

6.3.2  Analyse du résultat

Etant donné qu’il y a autant de côtés rouges que de côtés blancs, le problème suivant a la même réponse :
On tire une carte : le côté que nous voyons est blanc.
Quelle est la probabilité pour que l’autre côté soit rouge ?
ou encore :
On tire une carte : nous voyons un côté de cette carte.
Quelle est la probabilité pour que l’autre côté ne soit pas de la même couleur?
Cela revient à demander quelle est la probabilité pour que l’on ait tiré la carte bicolore. Comme il y a trois cartes dont une seule est bicolore, la probabilité cherchée est égale à 1/3.
On peut aussi traiter ce problème avec les probabilités conditionnelles :
soit Ω l’ensemble des faces visibles. On repére la face visible par 2 nombres le numéro de sa carte et son numéro de face (par exemple [1,0] désigne la face 0 de la carte 1 alors que [0,1] désigne la face 1 de la carte 0) on a
Ω={[0,0],[0,1],[1,0],[1,1],[2,0],[2,1]}.
Les trois premiers éléments de Ω ont comme face visible une face blanche, les trois derniers éléments de Ω sont comme face visible une face rouge.
Soit A l’évènement "le coté visible est rouge",
soit B l’évènement "le coté non visible est blanc",
soit C l’évènement "le coté visible est rouge et le coté non visible est blanc" ou "le coté visible est blanc et le coté non visible est rouge" (ie la carte tirée est bicolore).
P(A)= 1/2
P(B)= 1/2
P(C)= 1/3
P(A et B)= 1/6
P(C)=P(A et B)+P(nonA et nonB)= 1/3
P(B/A)=P(A et B)/P(A)= 1/6/ 1/2= 1/3
On peut aussi numéroter les faces rouges et les faces blanches et dire qu’un couple represente une carte et le premier élément du couple est la face visible.
Par exemple, (R₃,B₃) représente la carte bicolore ayant comme face visible la face rouge.
Ω={(R₁,R₂),(R₂,R₁),(R₃,B₃),(B₃,R₃),(B₁,B₂),(B₂,B₁)}.
Soit A l’évènement "le coté visible est rouge" :
A={(R₁,R₂),(R₂,R₁),(R₃,B₃)}
Donc :
P(A)= 1/2
soit B l’évènement "le coté non visible est blanc" :
A et B={(R₃,B₃)}
Donc :
P(A et B)= 1/6
Donc :
P(B/A)=P(A et B)/P(A)= 1/6/ 1/2= 1/3

6.4  Les quatre cartes bicolores

On met dans un chapeau quatre cartes : une des cartes a deux côtés blancs, une autre a un côté rouge et un côté blanc et les deux restantes ont deux côtés rouges.
On tire une carte : le côté que nous voyons est rouge.
Quelle est la probabilité pour que l’autre côté soit blanc ?

6.4.1  Simulation

cartebic4(n):={
  local C,a,b,nbi;
  C:=[[0,0],[0,1],[1,1],[1,1]];
  nbi:=0
  for (k:=0;k<n;k++){
    a:=rand(4);
    b:=rand(2);
    while (C[a,b]==0) {
      a:=rand(4);
      b:=rand(2);
    }
    if (C[a,irem(b+1, 2)]==0) {
      nbi:=nbi+1;
    }
  }
  return(evalf(nbi/n));
};

On a obtenu :
cartebic4(300)= 0.18
cartebic4(3000)= 0.203666666667
cartebic4(30000)=0.2019

6.4.2  Analyse du résultat

On va traiter ce problème avec les probabilités conditionnelles :
soit Ω l’ensemble des faces visibles.
On repére la face visible par 2 nombres le numéro de sa carte et son numéro de face (par exemple [1,0] désigne la face 0 de la carte 1 alors que [0,1] désigne la face 1 de la carte 0) on a
Ω={[0,0],[0,1],[1,0],[1,1],[2,0],[2,1],[3,0],,[3,1]}.
Onsuppose que la carte 0 a 2 faces blanches,que la face 0 de la carte 1 est blanche et que sa face 1 est rouge et que les cartes 2 et 3 ont 2 faces rouges. Donc les trois premiers éléments de Ω sont des faces blanches, les cinq derniers éléments de Ω sont des faces rouges.
Soit A l’évènement "le coté visible est rouge",
soit B l’évènement "le coté non visible est blanc",
soit C l’évènement la carte tirée est bicolore.
P(A)= 5/8
P(B)= 3/8
P(A et B)= 1/8
P(C)=P(A et B)+P(nonA et nonB)= 1/4
P(B/A)=P(A et B)/P(A)= 1/8/ 5/8= 1/5.
Donc la probabilité que la face cachée soit blanche sachant que la face visible est rouge est : 1/5
Etant donné qu’il n’y a pas autant de côtés rouges que de côtés blancs, le problème posé n’est pas le même que :
On tire une carte : le côté que nous voyons est blanc.
Quelle est la probabilité pour que l’autre côté soit rouge ?
On a :
P(nonA)= 3/8
P(nonB)= 5/8
P(nonA et nonB)= 1/8
P(nonB/nonA)=P(nonA et nonB)/P(nonA)= 1/8/3/8= 1/3.
On retrouve la même probabilité que dans le cas des trois cartes bicolores car la probabilité demandée ne tient compte que de l’ensemble des cartes qui ont un côté blanc et dans les deux problèmes cet ensemble est le même.
ce n’est pas non plus le même problème que :
On tire une carte : nous voyons un côté de cette carte.
Quelle est la probabilité pour que l’autre côté ne soit pas de la même couleur?
On demande ici la probabilité de tirer la carte bicolore c’est à dire : P(C)= 1/4
Remarque
P(C)=P(A)*P(B/A)+P(nonA)*P(nonB/nonA)=
P(A et B)+P(nonA et nonB)= 1/4=3/8*1/3+5/8*1/5

6.5  La voiture et les deux chèvres

Un candidat à un jeu doit choisir entre trois portes et gagne ce qui se trouve derrière la porte choisie. Il y a une voiture derrière une porte et une chèvre derrière chacune des deux autres portes. Le candidat choisit une porte et le présentateur qui connait la porte gagnante, ouvre une des deux portes restantes derrière laquelle se trouve une chèvre, et demande au candidat si il veut changer son choix. A votre avis le candidat a-t-il plus de chances de gagner la voiture en changeant systématiquement son choix ?
Pour répondre à cette question, commençons par une simulation.

6.5.1  Simulation

Le paramètre n représente le nombre de jeux.
ng1 est le nombre de fois où le candidat gagne quand il ne change jamais de choix (situation1) et
ng2 est le nombre de fois où le candidat gagne quand il change systématiquement de choix (situation2).
La porte où l’on met la voiture est tirée au hasard (v:=rand(3);P[v]:=1).
Le candidat choisit une porte au hasard (a:=rand(3)).
Si (a==v) il gagne dans la situation1 (ng1:=ng1+1) et perd dans la situation2 (ng2 reste inchangé).
Si (a!=v) il gagne dans la situation2 (ng2:=ng2+1) et perd dans la situation1 (ng1 reste inchangé).
Dans ce qui suit la variable P ne sert à rien et permet juste de visualiser les 3 portes (si P[n]==0, derrière la porte de numéro n il y a une chèvre, et si P[n]==1, derrière la porte de numéro n il y a une voiture).
On écrit le programme chevre qui compte le nombre de gains dans ng1 quand on ne change pas son choix et qui compte le nombre de gains dans ng2 quand on change systématiquement son choix.

chevre(n):={
local a,v,ng1,ng2;
ng1:=0;
ng2:=0
for (k:=0;k<n;k++){
\\on choisit la porte v o\`u l'on met la voiture
v:=rand(3);
P:=[0,0,0];
P[v]:=1;
//le candidat choisit une porte a
a:=rand(3);
if (a==v){ng1:=ng1+1;}
else {ng2:=ng2+1;}
}
return ([evalf(ng1/n),evalf(ng2/n)]);
};

On a obtenu : chevre(10000)= [0.3303,0.6697]

6.5.2  Analyse du résultat

La voiture est derrière la porte v.
Le candidat choisit une porte a au hasard.
Si (a==v) il gagne dans la situation1 et perd dans la situation2 et,
si (a!=v) il gagne dans la situation2 et perd dans la situation1.
On a donc :
P(a=v)= 1/3
et donc P(a!=v)=1-P(a=v)= 2/3
Le candidat a donc deux fois plus de chances de gagner s’il change son choix systématiquement !
Remarque
Pourtant malgré la simplicité de la situation, notre intuition semble en défaut ...
Si ce qui précéde ne vous a pas convaincu faites le même problème avec 100 portes (1 voiture et 99 chèvres) et le présentateur ouvre 98 portes derrière lesquelles il y a des chèvres : on comprend bien qu’en désignant une porte, la voiture a plus de chances (99 chances sur 100) d’être derrière les portes restantes, et en ouvrant les 98 portes le présentateur élimine 98 chèvres et donc derrière la porte restante il y a 99 chances sur 100 pour qu’il y ait la voiture.

6.6  Comment couper des spaghettis en trois ?

Voici l’énoncé d’un problème :
On coupe de façon aléatoire un spaghetti en trois morceaux. Quelle est la probabilité pour qu’avec les trois morceaux obtenus on puisse former un triangle ? Comment peut-on simuler cette situation ou autrement dit que veut dire "on coupe de façon aléatoire un spaghetti en trois morceaux" ?
On suppose dans ce qui suit le spaghetti de longueur 1.

• Première méthode : on choisit au hasard deux points x et y de [0,1].
• Deuxième méthode : on choisit au hasard un point x de [0,1], puis on choisit au hasard le point y dans [0,x].
• Troisième méthode : on choisit au hasard un point x de [0,1], puis on choisit au hasard l’un des segments [0,x] ou [x,1], puis on choisit au hasard le point y dans le segment choisi.
• Quatrième méthode : on choisit au hasard un point x de [0,1], puis on choisit le plus grand des segments [0,x] ou [x,1], puis on choisit au hasard le point y dans le segment choisi.

Ces différentes méthodes conduisent-elles au même résultat ?
Quelle est la méthode qui donne la plus forte probabilité ?
Pour répondre à ces questions commençons par des simulations.
Pour cela, il faut savoir répondre à la question : à quelles conditions trois segments de longueurs a, b et c=1−a−b forment-ils un triangle ?
Une condition necessaire et suffisante est que :
a<b+c et b−c<a et c−b<a ou encore que :
a<1−a et a+2b−1<a et 1−a−2b<a ou encore que :
a<0.5 et b<0.5 et 0.5<a+b

6.6.1  Simulation première méthode

On choisit au hasard deux points d’abscisses x et y de l’intervalle [0;1].
On note :
x et y les abscisses des points de coupures.
a et b la longueur du premier et du deuxième morceau de spaghetti.
t le nombre de triangles obtenus au bout de n essais.

spag1(n):={
  local x,y,a,b,t;
  t:=0;
  for (k:=1;k<=n;k++){
     x:=evalf(rand(2^30)/2^30);
     y:=evalf(rand(2^30)/2^30);
     if (x<y) {
        a:=x;
        b:=y-x;
     } else {
        a:=y;
        b:=x-y;
     }
     if ((a<0.5) and (b<0.5) and (a+b>0.5)) {
        t:=t+1;
     }
  }
  return(evalf(t/n));
}; 

On a trouvé pour n=30000 : 0.2506
On a trouvé pour n=300000 : 0.24965

6.6.2  Simulation deuxième méthode

On choisit au hasard un point d’abscisse x de l’intervalle [0;1], puis on choisit au hasard un point d’abscisse y de l’intervalle [0;x].
On note :
x et y les abscisses des points de coupures.
a et b la longueur du premier et du deuxième morceau de spaghetti.
t le nombre de triangles obtenus au bout de n essais.

spag2(n):={
  local x,y,a,b,t;
  t:=0;
  for (k:=1;k<=n;k++){
     x:=evalf(rand(2^30)/2^30);
     y:=evalf(rand(2^30)/2^30)*x;
     a:=y;
     b:=x-y;
     if ((a<0.5) and (b<0.5) and (a+b>0.5)) {
        t:=t+1;
     }
  }
  return(evalf(t/n));
}; 

On a trouvé pour n=30000 : 0.193266666667
On a trouvé pour n=300000 : 0.191666666667

6.6.3  Simulation troisième méthode

On choisit au hasard un point d’abscisse x de l’intervalle [0;1], puis on choisit au hasard l’intervalle [0;x] ou [x;1] puis, on choisit au hasard un point d’abscisse y dans l’intervalle choisi.
On note :
x et y les abscisses des points de coupures.
a et b la longueur du premier et du deuxième morceau de spaghetti.
t le nombre de triangles obtenus au bout de n essais.

spag3(n):={
  local x,y,a,b,t;
  t:=0;
  for (k:=1;k<=n;k++){
     x:=evalf(rand(2^30)/2^30);
     if (rand(2)==0){
       y:=evalf(rand(2^30)/2^30)*x;
       a:=y;
       b:=x-y;
     } else {
       y:=evalf(rand(2^30)/2^30)*(1-x)+x;
       a:=x;
       b:=y-x;
     }
     if ((a<0.5) and (b<0.5) and (a+b>0.5)) {
       t:=t+1;
     }
  }
  return(evalf(t/n));
}; 

On a trouvé pour n=30000 : 0.195533333333
On a trouvé pour n=300000 : 0.194083333333

6.6.4  Simulation quatrième méthode

On choisit au hasard un point d’abscisse x de l’intervalle [0;1], puis on choisit le plus grand des deux intervalles [0;x] ou [x;1] puis, on choisit au hasard un point d’abscisse y dans l’intervalle choisi.
On note :
x et y les abscisses des points de coupures.
a et b la longueur du premier et du deuxième morceau de spaghetti.
t le nombre de triangles obtenus au bout de n essais.

spag4(n):={
  local x,y,a,b,t;
  t:=0;
  for (k:=1;k<=n;k++){
     x:=evalf(rand(2^30)/2^30);
     if (x>0.5){
       y:=evalf(rand(2^30)/2^30)*x;
       a:=y;
       b:=x-y;
     } else {
       y:=evalf(rand(2^30)/2^30)*(1-x)+x;
       a:=x;
       b:=y-x;
     }
     if ((a<0.5) and (b<0.5) and (a+b>0.5)) {
       t:=t+1;
     }
  }
  return(evalf(t/n));
}; 

On a trouvé pour n=30000 : 0.388366666667
On a trouvé pour n=300000 : 0.385946666667
On remarque que :
0.194083333333*2 = 0.388166666666
0.191666666667*2 = 0.383333333334
ln(2)-0.5= 0.19314718056

6.6.5  Analyse des résultats

Première méthode

Première méthode : on choisit au hasard deux points x et y de [0,1].
On sait que si l’on obtient x<0.5, pour obtenir un triangle dans ce cas, il faut choisir y dans l’intervalle [1/2,x+1/2] qui est un intervalle de longueur x. La probabilité d’obtenir un y qui convient est donc alors égale à x.
On sait que si l’on obtient x>0.5, pour obtenir un triangle dans ce cas, il faut choisir y dans l’intervalle [x−1/2,1/2] qui est un intervalle de longueur 1−x. La probabilité d’obtenir un y qui convient est donc alors égale à 1−x.
Donc la probabilité d’obtenir un triangle est :
∫₀^1/2xdx+∫_1/2¹(1−x)dx=1/8+1/8=1/4

Deuxième méthode

Deuxième méthode : on choisit au hasard un point x de [0,1], puis on choisit au hasard le point y dans [0,x].
On sait que si l’on obtient x<0.5, on a une probabilité nulle d’obtenir un triangle puisque ensuite on choisit y vérifiant y<x. On sait que si l’on obtient x>0.5, pour obtenir un triangle dans ce cas, il faut choisir y dans l’intervalle [x−1/2,1/2] qui est un intervalle de longueur 1−x. La probabilité d’obtenir un y qui convient est donc égale à 1−x/x.
Donc la probabilité d’obtenir un triangle est :
∫_1/2¹1−x/xdx=ln(2)−1/2

Troisième méthode

Troisième méthode : on choisit au hasard un point x de [0,1], puis on choisit au hasard l’un des segments [0,x] ou [x,1], puis on choisit au hasard le point y dans le segment choisi.
Si on choisit avec une probabilité 0.5 l’un des deux segments [0,x[ ou [x,1[, si x<0.5 pour obtenir un y qui convient il faut choisir ( avec une probabilité de 0.5) l’intervalle [x,1[ (qui est un intervalle de longueur 1−x), puis choisir y dans l’intervalle [1/2,x+1/2] qui est un intervalle de longueur x et la probabilité d’obtenir un y qui convient est donc égale à 1/2*x/1−x.
Si x>0.5 pour obtenir un y qui convient il faut choisir ( avec une probabilité de 0.5) l’intervalle [0,x[ (de longueur x), puis choisir y dans l’intervalle [x−1/2,1/2] qui est un intervalle de longueur 1−x et la probabilité d’obtenir un y qui convient est donc égale à 1/2*1−x/x.
Donc la probabilité d’obtenir un triangle est :
1/2∫₀^1/2x/1−xdx+1/2∫_1/2¹1−x/xdx=1/2(ln(2)−1/2)+1/2(ln(2)−1/2)=ln(2)−1/2

Quatrième méthode

Quatrième méthode : on choisit au hasard un point x de [0,1], puis on choisit le plus grand des segments [0,x] ou [x,1], puis on choisit au hasard le point y dans le segment choisi.
Si x<0.5, on choisit y dans [x,1[ (de longueur 1−x), puis pour obtenir un y qui convient il faut le choisir dans l’intervalle [1/2,x+1/2] qui est un intervalle de longueur x et la probabilité d’obtenir un y qui convient est donc égale à x/1−x.
Si x>0.5, on choisit y dans [0,x[ (de longueur x), puis pour obtenir un y qui convient il faut le choisir dans l’intervalle [x−1/2,1/2] qui est un intervalle de longueur 1−x et la probabilité d’obtenir un y qui convient est donc égale à 1−x/x.
Donc la probabilité d’obtenir un triangle est :
∫₀^1/2x/1−xdx+∫_1/2¹1−x/xdx=ln(2)−1/2+ln(2)−1/2=2*ln(2)−1

Quelques questions

Lorsque x a été choisi, on choisit de placer y soit sur [0,x[ soit sur [x,1[ avec quelle probabilité doit-on faire ce choix pour avoir les cotés d’un triangle avec une probabilité de 0.25 ?
Il faut choisir le segment [0,x[ avec une probabilité de x et donc choisir le segment [x,1[ avec une probabilité de 1−x.
En effet la probabilité d’obtenir les 3 côtés d’un triangle est alors :
∫₀^1/2(1−x)*x/1−xdx+∫_1/2¹x*1−x/xdx= ∫₀^1/2xdx+∫_1/2¹(1−x)dx=1/8+1/8=1/4.
Voici la simulation :

spag5(n):={
  local x,y,a,b,t;
  t:=0;
  for (k:=1;k<=n;k++){
     x:=evalf(rand(2^30)/2^30);
     if (evalf(rand(2^30)/2^30)<x){
       y:=evalf(rand(2^30)/2^30)*x;
       a:=y;
       b:=x-y;
     } else {
       y:=evalf(rand(2^30)/2^30)*(1-x)+x;
       a:=x;
       b:=y-x;
     }
     if ((a<0.5) and (b<0.5) and (a+b>0.5)) {
       t:=t+1;
     }
  }
  return(evalf(t/n));
}; 

On a trouvé pour n=30000 : 0.2502
On a trouvé pour n=300000 : 0.251556666667
Que se passe-t-il si on choisit le segment [0,x[ avec une probabilité de 1−x et le segment [x,1[ avec une probabilité de x ?
Voici la simulation :

spag6(n):={
  local x,y,a,b,t;
  t:=0;
  for (k:=1;k<=n;k++){
     x:=evalf(rand(2^30)/2^30);
     if (evalf(rand(2^30)/2^30)<1-x){
       y:=evalf(rand(2^30)/2^30)*x;
       a:=y;
       b:=x-y;
     } else {
       y:=evalf(rand(2^30)/2^30)*(1-x)+x;
       a:=x;
       b:=y-x;
     }
     if ((a<0.5) and (b<0.5) and (a+b>0.5)) {
       t:=t+1;
     }
  }
  return(evalf(t/n));
}; 

On a trouvé pour n=30000 : 0.138533333333
On a trouvé pour n=300000 : 0.136773333333
Exercice : Montrer que de façon théorique, on trouve : 2*ln(2)-5/4
On vérifie : evalf(2*log(2)-5/4)=0.13629436112

6.6.6  Comment simuler l’expérimentation ?

première façon

Supposons que l’on fasse faire à un groupe de personnes l’expérimentation de la quatrième méthode (on recoupe le plus grand morceau). Lorsqu’une personne efféctue l’expérience la première cassure (celle qui détermine x) se fera en général entre h et 1−h : h étant l’emplacement des doigts. On suppose ensuite que l’emplacement des doigts nécessaire pour faire la cassure est proportionnel à la longueur donc si y se trouve sur [0,x[ la cassure se fera sur [hx,x−xh[.
On écrit donc la fonction suivant dépendant de n nombre d’expériences et h l’emplacement des doigts.

spagex(n,h):={
local x,y,a,b,t;
t:=0;
for (k:=1;k<=n;k++){
  x:=evalf(rand(2^30)/2^30);
  x:=h+x*(1-2*h);
  if (x>0.5){
    y:=h*x+evalf(rand(2^30)/2^30)*x*(1-2*h);
    a:=y;
    b:=x-y;
  } else {
    y:=(1-x)*h+evalf(rand(2^30)/2^30)*(1-x)*(1-2*h)+x;
    a:=x;
    b:=y-x;
  }
  if ((a<0.5) and (b<0.5) and (a+b>0.5)) {
    t:=t+1;
  }
}
return(evalf(t/n));
};

On trouve pour n=30 et h=0.08 : 0.6
On trouve pour n=3000 et h=0.08 : 0.626666666667
On trouve pour n=3000 et h=0.1 : 0.561
On trouve pour n=300 et h=0.1 : 0.535666666667
On trouvera dans le répertoire simulation, les valeurs du couple [x,y] trouvées lors de l’exécution de spag4(100) dans le fichier Asim et, les valeurs du couple [x,y] trouvées lors de l’exécution de spagex(100,0.1) dans le fichier Aex. Bien sûr, on doit rajouter dans ces deux programmes une variable globale dans laquelle on engrange les valeurs de [x,y].
Le calcul théorique de la probabilité d’obtenir un triangle est alors :
1/1−2h (∫_h^1/2 x/(1−x)*(1−2h)dx+∫_1/2^1/2−2h dx+∫_1/2−2h^1−h1−x/x(1−2h)dx)
ce qui donne la formule :
1/(1−2h)²(ln(2(1−h)²)+−6h²+9h−2/2(1−h)(1−2h)².
En effet,
- quand h<x<1/2, on choisit y dans ]x+(1−x)*h;1−(1−x)*h[ (segment de longueur (1−x)*(1−2*h)) on aura un triangle si 1/2<y<x+1/2 (segment de longueur x),
- quand 1/2<x<1/2−2h, on choisit y dans ]h.x;x−h.x[ on est sûr d’avoir un triangle car y<x−h*x<1/2,
- quand 1/2−2h<x<1−h, on choisit y dans ]h.x;x−h.x[ (intervalle de longueur x(1−2h)) on aura un triangle si 1/2−x<y<1/2 (intervalle de longueur 1−x).
d’ou les trois intégrales qu’il faut diviser par 1−2h car on choisit x dans ]h;1−h[ (intervalle de longueur 1−2h)

Une autre façon de simuler l’expérimentation

On peut aussi, par exemple, supposer que l’on coupe le spaghetti en suivant une loi de probabilité de densité f(x), avec comme graphe de f une parabole, par exemple, pour un spaghetti de longueur 1, on peut choisir :
f(x)=kx(1−x) pour x ∈ [0,1].
On doit donc avoir ∫₀¹f(t)dt=k/6=1 donc k=6.
On suppose donc que f(x)=6x(1−x) pour x ∈ [0,1]
On suppose que l’on recoupe le morceau le plus grand.
On a alors :
Soit F(x)=∫₀^xf(t)dt=3x²−2x³.
Si U est une variable aléatoire uniforme (donné par exemple par la fonction rand() de Xcas) on a :
X=F⁻¹(U) et,
Proba(U<F(x))=Proba(F⁻¹(U)<x)=Proba(X<x)=F(x).
Pour déterminer X selon cette loi, on cherche x vérifiant x=F^-1(u).
Dans le programme ci-dessous on note g la fonction F et on écrit :

g(v):=3*v^2-2*v^3;
u:=evalf(rand(2^30)/2^30);
j:=0.1;
while (x> g(j)){j:=j+0.1;}
x:=j-0.05;

on peut aussi écrire :

g(v):=3*v^2-2*v^3;
u:=evalf(rand(2^30)/2^30);
solve(g(x)=u,x)

Ainsi, si F(J-0.1)<U<F(J) on a J-0.1<F^-1(U)=X<J.
Pour choisir y dans l’intervalle [0;a] selon cette loi, la densité de probabilité correspondante est f_a(t)=6t(a−t)/a³ et F_a(t)=F(t/a).
Pour déterminer la loi de Y, lorsqu’on coupe un spaghetti de longueur x, selon cette loi, on écrit :

y:=evalf(rand(2^30)/2^30);
j:=0.1;
while (y> g(j)){j:=j+0.1;}
y:=(j-0.05)*x;

Si x∈ [1/2;1], et y∈[0;x], la probabilité d’avoir un triangle est que :
y∈[x−1/2;1/2].
Cherchons la probabilité d’avoir :
y∈[x−1/2;1/2], sachant que x∈ [1/2;1], et y∈[0;x].
On a :
Proba(y∈[x−1/2;1/2])=F_x(1/2)−F_x(x−1/2)=F(1/2x)−F((2x−1)/2x)=−2x³+3x−1/2x³
Pour le calcul théorique de la probabilité d’avoir un triangle, on utilise la symétrie : en effet, on a soit x∈ [1/2;1] et y∈[0;x] soit, x∈ [0;1/2] et y∈[x;1] (donc on fait le calcul de cette probabilité lorsque x∈ [1/2;1] et on multiplie par 2 cette probabilité pour avoir le résultat).
Donc la probabilité d’avoir un triangle, avec ce choix de découpage est :
2∫_1/2¹ f(x)(F(1/2x)−F((2x−1)/2x))dx
Puisque F(1/2x)−F((2x−1)/2x)=−2x³+3x−1/2x³, et que f(x)=6x(1−x), on tape :
normal(6*int((1-x)*(-2*x^3+3*x-1)/(x^2),x,1/2,1))
On obtient :
-24*log(1/2)-16
et avec la commande evalf on obtient :
0.635532333439
C’est à dire :
6∫_1/2¹(1−x)(−2x³+3x−1)/x² dx=(−24ln(1/2)−16) ≃ 0.635532333439
Voici le programme de simulation avec Xcas

spagb(n):={
//integrate(6*x*(1-x)*(g(0.5/x)-g(1-0.5/x)),x,0.5,1) 
local x,y,a,b,t;
t:=0;
g(u):=3*u^2-2*u^3;
//Ab:=[];
for (k:=1;k<=n;k++){
x:=evalf(rand(2^30)/2^30);

j:=0.1;while (x> g(j)){j:=j+0.1;}
x:=j-0.05;
y:=evalf(rand(2^30)/2^30);
j:=0.1;while (y> g(j)){j:=j+0.1;}
if (x>0.5){
y:=(j-0.05)*x;
a:=y;
b:=x-y;
} else {
y:=(j-0.05)*(1-x)+x;
a:=x;
b:=y-x;
}
//Ab:=append(Ab,[x,y]);
if ((a<0.5) and (b<0.5) and (a+b>0.5)) {
t:=t+1;
}
}
return(evalf(t/n));
};

6.7  La ration de pain

En un pays lointain, le pain était limité à 200 grammes par personne et par jour. Le boulanger ne fabriquait donc que des pains de 200 grammes pour ses 1000 clients. Chaque matin, un vieux professeur allait chez le boulanger chercher sa ration quotidienne. Un jour il dit au boulanger :
- "Vous volez vos clients, les pains que vous vendez sont 1 pour cent plus petits qu’ils ne devraient l’être et vous devez donc donner à tous vos clients un pain gratuit tous les 100 jours".
- "Mais Monsieur, dit le boulanger tous les pains ne peuvent pas tous avoir le même poids ! Certains sont quelquefois, quelques pour cent plus lourds et d’autres quelques pour cent plus légers !"
- "Depuis 100 jours, je pèse mon pain et j’ai obtenu une courbe de Gauss de moyenne un poids de 198.04 grammes, et c’est inadmissible ! Si vous ne modifiez pas le poids de vos pains, je le signalerai à la répression des fraudes"
- "Je vous promets de faire le nécessaire dès demain"
Le Boulanger ne voulait pas changer sa manière de faire et chaque matin, avant le passage du professeur, il choisissait un pain et le pesait : s’il pesait au moins 200 grammes il le mettait de côté pour le professeur, sinon il en choisissait un autre jusqu’à obtenir un pain d’au moins 200 grammes qu’il mettait de côté pour le professeur. Cent jours plus tard, le professeur dit :
- "Vous n’avez rien changé ! vous continuez à voler vos clients"
"Mais Monsieur, vous ne pouvez rien prouver car tous les pains que je vous ai donnés ces derniers mois pesaient tous au moins 200 grammes"
- "Justement si !"
Pouvez-vous trouver l’argument du professeur ?

6.7.1  Simulation avec une loi binomiale

Simulation de la fabrication des pains

Voici un programme qui fabrique n pains dont le poids en grammes est dans l’intervalle [192,204] et suit une loi binomiale de moyenne 198.
On utilise pour cela la loi binomiale : on peut se servir de la simulation du parcours sur un axe (cf 6.2.1) : pour fabriquer un pain on ajoute à 192 le nombre de faces obtenu quand on lance 12 fois de suite une pièce.
Contrairement, au parcours on ne classe pas les pains par leur poids, on met les poids des n pains fabriqués dans une liste A.

pain(n) :={
  local T,r,A,j,k;
  A:=makelist(x->192,1,n,1);
  for (j:=0;j<n;j++){
    r:=rand(2); 
    T:=0;
    for (k:=0;k<12;k++){
      if (r==1){
        T:=T+1;
      }
    r:=rand(2);
    }
  A[j]:=A[j]+T;
  }
return(A);
}; 

Un exemple de fournée de 100 pains:
pain(100) = [197,199,199,198,197,199,196,199,199,
196,199,198,195,196,197,198,199,198,197,198,197,201,202,196,200,
201,197,195,200,200,197,198,196,199,197,196,197,201,198,198,199,
201,202,201,199,201,197,200,197,199,196,201,201,197,199,199,195,
198,199,199,198,198,200,195,198,197,199,200,200,196,195,199,197,
200,200,201,200,199,198,198,200,199,199,198,197,197,200,199,198,
195,199,198,198,198,197,200,195,198,200,196]
En théorie on aurait du avoir :
0 pains de poids 193 g et 0 de poids 203 g
2 pains de poids 194 g et 2 de poids 202 g
5.5 pains de poids 195 g et 5.5 de poids 201 g
12 pains de poids 196 g et 12 de poids 200 g
19 pains de poids 197 g et 19 de poids 199 g
23 pains de poids 198 g

Simulation de la pesée du professeur

Remarque
Pour la simulation, on ne refait pas le pain tous les jours !
A:=pain(n);
est mis au début, et non dans la boucle (là où il est commenté), car sinon le programme est trop long à l’exécution.
p représente le nombre de jours pendant lesquels on effectue la pesée et pj représente le poids obtenu chaque jour.
On classe ces poids dans P : P[0] est égal au nombre de pains de poids 192 grammes, P[1] est égal au nombre de pains de poids 193 grammes... m est alors la moyenne des poids obtenus.

client(p,n):={
local pj,A,P,D,j,k,m;
P:=makelist(x->0,0,12,1);
A:=pain(n);
S:=0;
for (k:=0;k<p;k++){
    //A:=pain(n);
    j:=rand(n); 
    pj:=A[j];
    S:=S+pj;
    pj:=pj-192;
    P[pj]:=P[pj]+1;
};
m:=evalf(S/p);
print(P);
print(m);
xyztrange(-0.2,12.2,-1,36,-10,10,-10,-10,-0.2,12.2,
          -1,36,1);
return segment(0,i*P[0]),segment(1,1+i*P[1]),
 segment(2,2+i*P[2]),segment(3,3+i*P[3]),
 segment(4,4+i*P[4]),segment(5,5+i*P[5]),
 segment(6,6+i*P[6]),segment(7,7+i*P[7]),
 segment(8,8+i*P[8]),segment(9,9+i*P[9]),
 segment(10,10+i*P[10]),segment(11,11+i*P[11]),
 segment(12,12+i*P[12]);
}; 

On tape :
client(100,1000)
On obtient écrit en bleu :
P:[0,0,6,7,10,22,15,20,11,8,1,0,0]
m=197.83
En théorie on doit avoir :
3 pains de poids 193 g et 3 de poids 203 g
16 pains de poids 194 g et 16 de poids 202 g
54 pains de poids 195 g et 54 de poids 201 g
121 pains de poids 196 g et 121 de poids 200 g
193 pains de poids 197 g et 193 de poids 199 g
225 pains de poids 198 g
Voici le "diagramme en bâtons" de la distribution des pains que le professeur a obtenu :

Il suffit de rajouter la ligne dans le programme précédent (au bon enfroit!) :
while (pj<200) {j:=rand(n); pj:=A[j];}
qui permet de choisir un pain de poids supérieur ou égal à 200 grammes.

chouchou(p,n):={
  local pj,A,P,S,j,k,m;
  P:=makelist(x->0,0,12,1);
  A:=pain(n);
  S:=0;
  for (k:=0;k<p;k++){
    //A:=pain(n);
    j:=rand(n); 
    pj:=A[j];
    //si le poids pj<200g on prend un autre pain
    while (pj<200) {j:=rand(n); pj:=A[j];}
    S:=S+pj;
    pj:=pj-192;
    P[pj]:=P[pj]+1;
  };
  m:=evalf(S/p);
  print(P);
  print(m);
  xyztrange(-0.2,12.2,-1,62.5,-10,10,-10,-10,-0.2,
            12.2,-1,60,1);
  return segment(0,i*P[0]),segment(1,1+i*P[1]),
    segment(2,2+i*P[2]),segment(3,3+i*P[3]),
    segment(4,4+i*P[4]),segment(5,5+i*P[5]),
    segment(6,6+i*P[6]),segment(7,7+i*P[7]),
    segment(8,8+i*P[8]),segment(9,9+i*P[9]),
    segment(10,10+i*P[10]),segment(11,11+i*P[11]),
    segment(12,12+i*P[12]);
};   

On tape : chouchou(100,1000)
On obtient écrit en bleu :
P=[0,0,0,0,0,0,0,0,61,29,6,4,0]
m=200.53
et le "diagramme en bâtons" de la distribution des pains que le professeur a obtenu a été le suivant :

6.7.2  Analyse du résultat

6.7.3  Simulation avec une loi gaussienne

On considère que le poids des pains du boulanger suit une loi gaussienne de moyenne 198 grammes et d’écart type σ grammes.

Simulation avec rand()

Le nombre de pains de poids x est donc approximativement de :

Pour σ=2 on a :
f(192)=f(204)=0.002 f(193)=f(203)=0.009 f(194)=f(202)=0.027 f(195)=f(201)=0.065 f(196)=f(200)=0.121 f(197)=f(199)=0.176 f(198)=0.200

et on a bien f(192)+f(193)+...+f(204)=1
Voici une fournée de 1000 pains selon cette répartition représentée par la liste G des poids de ces 1000 pains.

//f(x):=0.5/sqrt(2*pi)*exp(-0.125*(x-198)^2)
G:=[192,204,192,204];
for(j:=0;j<9;j++){
G:=concat(G,[193,203]);
};
for(j:=0;j<27;j++){
G:=concat(G,[194,202]);
};
for(j:=0;j<65;j++){
G:=concat(G,[195,201]);
};
for(j:=0;j<121;j++){
G:=concat(G,[196,200]);
};
for(j:=0;j<176;j++){
G:=concat(G,[197,199]);
};
for(j:=0;j<200;j++){
G:=concat(G,[198]);
};

La fournée G de 10000 pains se trouve dans le fichier painG.
Le professeur achéte p pains (par exemple p=100).

prof(p):={
local pj,A,P,j,m,S,k;
P:=makelist(0,0,12,1);
A:=G;
S:=0;
for (k:=0;k<p;k++){
    j:=rand(1000); 
    pj:=A[j];
    S:=S+pj;
    pj:=pj-192;
    P[pj]:=P[pj]+1;
};
m:=evalf(S/p);
print(P);
print(m);
return segment(0,i*P[0]),segment(1,1+i*P[1]),
 segment(2,2+i*P[2]),segment(3,3+i*P[3]),
 segment(4,4+i*P[4]),segment(5,5+i*P[5]),
 segment(6,6+i*P[6]),segment(7,7+i*P[7]),
 segment(8,8+i*P[8]),segment(9,9+i*P[9]),
 segment(10,10+i*P[10]),segment(11,11+i*P[11]),
 segment(12,12+i*P[12]);
};  

Le pain du professeur a un poids (en grammes) toujours supérieur ou égal à 200.

profchou(p):={
local pj,A,P,j,m,S,k;
P:=makelist(0,0,12,1);
A:=G;
S:=0;
for (k:=0;k<p;k++){
    j:=rand(1000); 
    pj:=A[j];
    while (pj<200) {j:=rand(n); pj:=A[j];}
    S:=S+pj;
    pj:=pj-192;
    P[pj]:=P[pj]+1;
};
m:=evalf(S/p);
print(P);
print(m);
return segment(0,i*P[0]),segment(1,1+i*P[1]),
 segment(2,2+i*P[2]), segment(3,3+i*P[3]),
 segment(4,4+i*P[4]),segment(5,5+i*P[5]), 
 segment(6,6+i*P[6]),segment(7,7+i*P[7]),
 segment(8,8+i*P[8]), segment(9,9+i*P[9]),
 segment(10,10+i*P[10]),segment(11,11+i*P[11]),
 segment(12,12+i*P[12]);
};  

Simulation avec randnorm()

Pour simuler une fournée du boulanger, on va utiliser randnorm(198,2) Le professeur achéte p pains (par exemple p=100)

profnorm(p):={
local pj,P,j,m,S,k;
P:=makelist(0,0,12,1);
S:=0;
for (k:=0;k<p;k++){
    pj:=floor(randnorm(198,2)); 
    S:=S+pj;
    pj:=pj-192;
    if (pj<0) {P[0]:=P[0]+1;} 
          else
          {if (pj>12) {P[12]:=P[12]+1;}
               else
               {P[pj]:=P[pj]+1;}
           }
};
m:=evalf(S/p);
return([P,m,segment(0,i*P[0]),segment(1,1+i*P[1]),
 segment(2,2+i*P[2]),segment(3,3+i*P[3]),
 segment(4,4+i*P[4]),segment(5,5+i*P[5]),
 segment(6,6+i*P[6]),segment(7,7+i*P[7]),
 segment(8,8+i*P[8]),segment(9,9+i*P[9]),
 segment(10,10+i*P[10]),segment(11,11+i*P[11]),
 segment(12,12+i*P[12])]);
};  

Puis on tape par exemple :
profnorm(100) écrit en bleu :
P=[0,0,0,0,0,0,0,0,61,29,6,4,0]
m=200.53
et le "diagramme en bâtons" de la distribution des pains On obtient écrit en bleu :
P:[0,2,5,7,13,25,14,16,8,6,3,0,1]
m:197.66
et le "diagramme en bâtons" de la distribution des pains selon la loi normale de moyenne 198 et d’écart-type 2 :

On écrit ensuite le programme profchounorm pour simuler le poids du pain du professeur lorsque ce pain a toujours un poids (en grammes) supérieur ou égal à 200.

profchounorm(p):={
  local pj,P,j,m,S,k;
  P:=makelist(0,0,12,1);
  S:=0;
  for (k:=0;k<p;k++){
    pj:=floor(randnorm(198,2)); 
    while (pj<200) {pj:=floor(randnorm(198,2));}
    S:=S+pj;
    pj:=pj-192;
    if (pj<0) 
     {P[0]:=P[0]+1;} 
    else
     {if (pj>12) {P[12]:=P[12]+1;}
      else
       {P[pj]:=P[pj]+1;}
     };
  };
  m:=evalf(S/p);
  print(P);
  print(m);
  return segment(0,i*P[0]),segment(1,1+i*P[1]),
  segment(2,2+i*P[2]),segment(3,3+i*P[3]),
  segment(4,4+i*P[4]),segment(5,5+i*P[5]),
  segment(6,6+i*P[6]),segment(7,7+i*P[7]),
  segment(8,8+i*P[8]),segment(9,9+i*P[9]),
  segment(10,10+i*P[10]),segment(11,11+i*P[11]),
  segment(12,12+i*P[12]);
};  

On valide ce programme, puis on tape par exemple :
profchounorm(100)
On obtient écrit en bleu :
P=[0,0,0,0,0,0,0,0,60,27,8,4,1]
m=200.59
et le "diagramme en bâtons" de la distribution des pains selon la loi normale de moyenne 198 et d’écart-type 2, pour des poids p>=200.