Permutations

A permutation p of size n is a bijection from [0..n - 1] on [0..n - 1] and is represented by the list : [p(0), p(1), p(2)...p(n - 1)].
For example, the permutation p represented by [1, 3, 2, 0] is the application from [0, 1, 2, 3] on [0, 1, 2, 3] defined by :

p(0) = 1, p(1) = 3, p(2) = 2, p(3) = 0

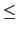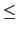A cycle c of size p is represented by the list [a₀,..., a_p-1] ( 0 $\leq$ a_k $\leq$ n - 1) it is the permutation such that

c(a_i) = a_i+1 for (i = 0..p - 2),    c(a_p-1) = a₀,    c(k) = k otherwise

A cycle c is represented by a list and a cycle decomposition is represented by a list of lists.
For example, the cycle c represented by the list [3, 2, 1] is the permutation c defined by c(3) = 2, c(2) = 1, c(1) = 3, c(0) = 0 (i.e. the permutation represented by the list [0, 3, 1, 2]).