




suivant: Airy functions : Airy_Ai
monter: Real numbers
précédent: Derivatives of the DiGamma
Table des matières
Index
The 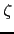 function : Zeta
function : Zeta
Zeta takes as argument a real x.
Zeta returns for x > 1 :
and for x < 1 it's meromorphic continuation.
Input :
Zeta(2)
Output :
pi^2/6
Input :
Zeta(4)
Output :
pi^4/90
giac documentation written by Renée De Graeve and Bernard Parisse