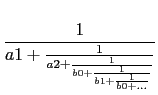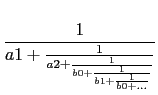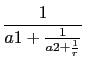Continued fraction representation of a real : dfc

dfc takes as argument a real or a rational or a floating point number a and an integer n (or a real epsilon).
dfc returns the list of the continued fraction representation of a of order n (or with precision epsilon i.e. the continued fraction representation which approachs a or evalf(a) with precision epsilon, by default epsilon is the value of the epsilon defined in the cas configuration with the menu Cfg $\blacktriangleright$Cas Configuration).
convert with the option confrac has a similar functionnality: in that case the value of epsilon is the value of the epsilon defined in the cas configuration with the menu Cfg $\blacktriangleright$Cas Configuration (see 1.21.23) and the answer may be stored in an optionnal third argument.

Remarks

• If the last element of the result is a list, the representation is ultimaltely periodic, and the last element is the period. It means that the real is a root of an equation of order 2 with integer coefficients.
• if the last element of the result is not an integer, it represents a remainder r ( a = a0 + 1/.... + 1/an + 1/r). Be aware that this remainder has lost most of it's accuracy.

If dfc(a)=[a0,a1,a2,[b0,b1] that means :

a = a0 + $${\frac{{1}}{{a1+\frac{1}{a2+\frac{1}{b0+\frac{1}{b1+\frac{1}{b0+...}}}}}}}$$

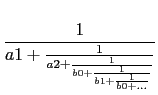
If dfc(a)=[a0,a1,a2,r] that means :

a = a0 + $${\frac{{1}}{{a1+\frac{1}{a2+\frac{1}{r}}}}}$$

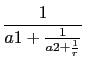
Input :

dfc(sqrt(2),5)

Output :

[1,2,[2]]

Input :

dfc(evalf(sqrt(2)),1e-9)

Or :

dfc(sqrt(2),1e-9)

Output :

[1,2,2,2,2,2,2,2,2,2,2,2,2]

Input :

convert(sqrt(2),confrac,'dev'

Output (if in the cas configuration epsilon=1e-9) :

[1,2,2,2,2,2,2,2,2,2,2,2,2]

and [1,2,2,2,2,2,2,2,2,2,2,2,2] is stored in dev.
Input :

dfc(9976/6961,5)

Output :

[1,2,3,4,5,43/7]

Input to verify:
1+1/(2+1/(3+1/(4+1/(5+7/43))))
Output :
9976/6961
Input :

convert(9976/6961,confrac,'l')

Output (if in the cas configuration epsilon=1e-9) :

[1,2,3,4,5,6,7]

and [1,2,3,4,5,6,7] is stored in l
Input :

dfc(pi,5)

Output :

[3,7,15,1,292,(-113*pi+355)/(33102*pi-103993)]

Input :

dfc(evalf(pi),5)

Output (if floats are hardware floats, e.g. for Digits=12) :

[3,7,15,1,292,1.57581843574]

Input :

dfc(evalf(pi),1e-9)

Or :

dfc(pi,1e-9)

Or (if in the cas configuration epsilon=1e-9) :

convert(pi,confrac,'ll')

Output :

[3,7,15,1,292]