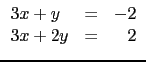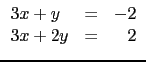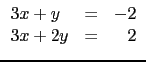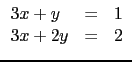suivant: Step by step Gauss-Jordan
monter: Linear systems
précédent: Gauss-Jordan reduction: rref gaussjord
Table des matières
Index
Solving A*X=B : simult
simult is used to solve a linear system of equations (resp.
several linear systems of equations with the same matrix A) written
in matrix form (see also 1.31.17) :
A*X=b (resp A*X=B)
simult takes as arguments the matrix A of the system and the
column vector (i.e. a one column matrix) b of the second
member of the system (resp.
the matrix B whose columns are the
vectors b of the second members of the different systems).
The result is a column vector, solution of the system (resp. a matrix
whose columns are the solutions of the different systems).
For example, to solve the system :
input :
simult([[3,1],[3,2]],[[-2],[2]])
Output :
[[-2],[4]]
Hence x = - 2 and y = 4 is the solution.
Input :
simult([[3,1],[3,2]],[[-2,1],[2,2]])
Output :
[[-2,0],[4,1]]
Hence x = - 2 and y = 4 is the solution of
whereas x = 0 and y = 1 is the solution of





suivant: Step by step Gauss-Jordan
monter: Linear systems
précédent: Gauss-Jordan reduction: rref gaussjord
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse