LU decomposition : lu

lu takes as argument a square matrix A of size n (numeric or symbolic).
lu(A) returns a permutation p of 0..n - 1, a lower triangular matrix L, with 1 on the diagonal, and an upper triangular matrix U, such that :

• P*A = L*U where P is the permutation matrix associated to p (that may be computed by P:=permu2mat(p)),
• the equation A*x = B is equivalent to :
  L*U*x = P*B = p(B) where p(B) = [b_p(0), b_p(1)..b_p(n-1)],    B = [b₀, b₁..b_n-1]

The permutation matrix P is defined from p by :

P[i, p(i)] = 1,    P[i, j] = 0 if j 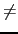 $$\neq$$  p(i)

In other words, it is the identity matrix where the rows are permuted according to the permutation p. The function permu2mat may be used to compute P (permu2mat(p) returns 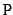$\tt P$).
Input :

(p,L,U):=lu([[3.,5.],[4.,5.]])

Output :

[1,0],[[1,0],[0.75,1]],[[4,5],[0,1.25]]

Here n = 2, hence :

P[0, p(0)] = P₂[0, 1] = 1,    P[1, p(1)] = P₂[1, 0] = 1,    P = [[0, 1],[1, 0]]

Verification :
Input :

permu2mat(p)*A; L*U

Output:

[[4.0,5.0],[3.0,5.0]],[[4.0,5.0],[3.0,5.0]]

Note that the permutation is different for exact input (the choice of pivot is the simplest instead of the largest in absolute value).
Input :

lu([[1,2],[3,4]])

Output :

[1,0],[[1,0],[3,1]],[[1,2],[0,-2]]

Input :

lu([[1.0,2],[3,4]])

Output :

[1,0],[[1,0],[0.333333333333,1]],[[3,4], [0,0.666666666667]]