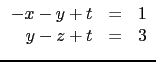suivant: Different matrix norm
monter: Linear Programmation
précédent: Linear Programmation
Table des matières
Index
The simple case
The function simplex_reduce makes the reduction
by the simplex algorithm to find :
max(
c.
x),
A.
x 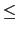 b
b,
x 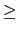
0,
b 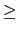
0
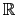 n, b
n, b 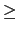 0 is a vector of
0 is a vector of
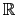 p and A is a matrix of p rows and n columns.
p and A is a matrix of p rows and n columns.
simplex_reduce takes as argument A,b,c et
returns max(c.x), the augmented solution of x
(augmented since the algorithm works by adding rows(A) auxiliary
variables) and the reduced matrix.
Example
Find
max(
X + 2
Y) where
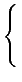
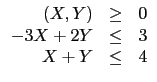
simplex_reduce([[-3,2],[1,1]],[3,4],[1,2])
Output :
7,[1,3,0,0],[[0,1,1/5,3/5,3],[1,0,(-1)/5,2/5,1], [0,0,1/5,8/5,7]]
Which means that the maximum of X+2Y under these conditions
is 7, it is obtained for X=1,Y=3
because [1,3,0,0] is the augmented solution and the reduced matrix is :
[[0,1,1/5,3/5,3],[1,0,(-1)/5,2/5,1], [0,0,1/5,8/5,7]].
A more complicate case that reduces to the simple case
With the former call of simplex_reduce, we have to :
- rewrite constraints to the form
xk
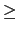 0,
0,
- remove variables without constraints,
- add variables such that all the constraints have positive components.
For example, find :
min(2
x +
y -
z + 4) where
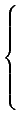
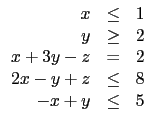
or to find the minimum of :
(-
X - 2
Y + 3) where
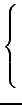
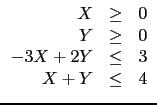
The general case
A linear programming problem may not in general be directly
reduced like above to the simple case. The reason is that
a starting vertex must be found before applying the simplex
algorithm. Therefore,
simplex_reduce may be called by specifying this starting
vertex, in that case, all the arguments including the starting
vertex are grouped in a single matrix.
We first illustrate this kind
of call in the simple case where the starting point does not
require solving an auxiliary problem.
If A has p rows and n columns and if we define :
B:=augment(A,idn(p)); C:=border(B,b);
d:=append(-c,0$(p+1)); D:=augment(C,[d]);
simplex_reduce may be called with D as single argument.
For the previous example, input :
A:=[[-3,2],[1,1]];B:=augment(A,idn(2)); C:=border(B,[3,4]);
D:=augment(C,[[-1,-2,0,0,0]])
Here
C=[[-3,2,1,0,3],[1,1,0,1,4]]
and D=[[-3,2,1,0,3],[1,1,0,1,4],[-1,-2,0,0,0]]
Input :
simplex_reduce(D)
Output is the same result as before.
Back to the general case.
The standard form of a linear programming problem is similar
to the simplest case above, but with Ax = b (instead of Ax 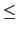 b)
under the conditions x
b)
under the conditions x 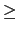 0. We may further assume that b
0. We may further assume that b 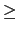 0
(if not, one can change the sign of the corresponding line).
0
(if not, one can change the sign of the corresponding line).
- The first problem is to find an x in the
Ax = b, x
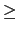 0 domain.
Let m be the number of lines of A. Add artificial variables
y1,..., ym and maximize
-
0 domain.
Let m be the number of lines of A. Add artificial variables
y1,..., ym and maximize
- 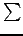 yi under the conditions
Ax = b, x
yi under the conditions
Ax = b, x 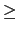 0, y
0, y 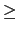 0
starting with initial value 0 for x variables
and y = b
(to solve this with Xcas, call
0
starting with initial value 0 for x variables
and y = b
(to solve this with Xcas, call simplex_reduce with
a single matrix argument obtained by augmenting A by the
identity, b unchanged and an artificial
c with 0 under A and 1 under the identity).
If the maximum exists and is 0, the identity submatrix above the last
column corresponds to an x solution, we may forget the artificial
variables (they are 0 if the maximum is 0).
- Now we make a second call to
simplex_reduce
with the original c and the value of x we found in the domain.
- Example : find the minimum of 2x + 3y - z + t with
x, y, z, t
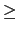 0 and :
0 and :
This is equivalent to find the opposite of the maximum of
- (2x + 3y - z + t).
Let us add two artificial variables y1 and y2,
simplex_reduce([[-1,-1,0,1,1,0,1],
[0,1,-1,1,0,1,3],
[0,0,0,0,1,1,0]])
Output: optimum=0, artificial variables=0, and the matrix
Columns 2 and 4 are the columns of the identity (in lines 1 and 2).
Hence
x = (0, 1, 0, 2) is an initial point in the domain.
We are reduced to solve the initial problem, after replacing the
lines of Ax = b by the two first lines of the answer above,
removing the last columns corresponding to the artificial variables.
We add c.x as last line
simplex_reduce([[-1/2,0,-1/2,1,2],
[1/2,1,-1/2,0,1],[2,3,-1,1,0]])
Output: maximum=-5, hence the minimum of the opposite is 5,
obtained for (0, 1, 0, 2), after replacement
x = 0, y = 1, z = 0 and t = 2.
For more details, search google for simplex algorithm.





suivant: Different matrix norm
monter: Linear Programmation
précédent: Linear Programmation
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
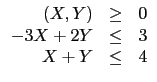
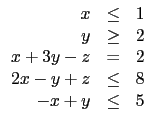
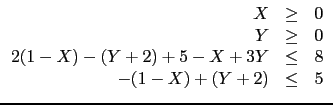
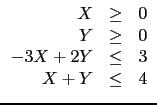
![]() b)
under the conditions x
b)
under the conditions x ![]() 0. We may further assume that b
0. We may further assume that b ![]() 0
(if not, one can change the sign of the corresponding line).
0
(if not, one can change the sign of the corresponding line).