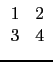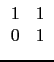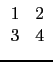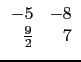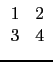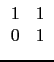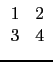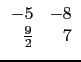Equivalent matrix : changebase

changebase takes as argument a matrix A and a change-of-basis matrix P.
changebase returns the matrix B such that B = P^-1AP.
Input :

changebase([[1,2],[3,4]],[[1,0],[0,1]])

Output :

[[1,2],[3,4]]

Input :

changebase([[1,1],[0,1]],[[1,2],[3,4]])

Output :

[[-5,-8],[9/2,7]]

Indeed :

$$\left[\vphantom{\begin{array}{rr} 1 & 2\\ 3&4\end{array}}\right.$$$$\begin{array}{rr} 1 & 2\\ 3&4\end{array}$$$$\left.\vphantom{\begin{array}{rr} 1 & 2\\ 3&4\end{array}}\right]^{{{-1}}}_{{}}$$*$$\left[\vphantom{\begin{array}{rr}1 & 1\\ 0&1\end{array}}\right.$$$$\begin{array}{rr}1 & 1\\ 0&1\end{array}$$$$\left.\vphantom{\begin{array}{rr}1 & 1\\ 0&1\end{array}}\right]$$*$$\left[\vphantom{\begin{array}{rr} 1 & 2\\ 3&4\end{array}}\right.$$$$\begin{array}{rr} 1 & 2\\ 3&4\end{array}$$$$\left.\vphantom{\begin{array}{rr}1 & 2\\ 3&4\end{array}}\right]$$ = $$\left[\vphantom{\begin{array}{rr}-5 & -8\\ \frac{9}{2}&7\end{array}}\right.$$$$\begin{array}{rr}-5 & -8\\ \frac{9}{2}&7\end{array}$$$$\left.\vphantom{\begin{array}{rr}-5 & -8\\ \frac{9}{2}&7\end{array}}\right]$$

.