



suivant: Exact bounds for real
monter: Exact roots of a
précédent: Exact roots of a
Table des matières
Index
Exact bounds for complex roots of a polynomial :
complexroot
complexroot takes 2 or 4 arguments : a polynomial and a real
number 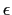 and optionnally two complex numbers
and optionnally two complex numbers
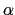 ,
,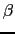 .
.
complexroot returns a list of vectors.
- If complexroot has 2 arguments,
the elements of each vector are
- either an interval (the
boundaries of this interval are the opposite vertices of a rectangle with sides
parallel to the axis and containing a complex root of the polynomial) and the
multiplicity of this root.
Let the interval be
[a1 + ib1, a2 + ib2] then
| a1 - a2| < 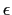 ,
| b1 - b2| <
,
| b1 - b2| < 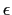 and the root a + ib verifies
a1
and the root a + ib verifies
a1 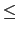 a
a 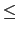 a2 and
b1
a2 and
b1 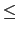 b
b 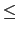 b2.
b2.
- or the value of an exact complex root of
the polynomial and the multiplicity of this root
- If complexroot has 4 arguments, complexroot returns a list of
vectors as above, but only for the roots lying in
the rectangle with sides parallel to the axis having
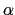 ,
,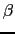 as
opposite vertices.
as
opposite vertices.
To find the roots of x3 + 1, input:
complexroot(x^3+1,0.1)
Output :
[[-1,1],[[(4-7*i)/8,(8-13*i)/16],1],[[(8+13*i)/16,(4+7*i)/8],1]]
Hence, for x3 + 1 :
- -1 is a root of multiplicity 1,
- 1/2+i*b is a root of multiplicity 1 with
-7/8
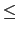 b
b 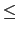 - 13/16,
- 13/16,
- 1/2+i*c is a root of multiplicity 1 with
13/1
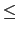 c
c 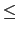 7/8.
7/8.
To find the roots of x3 + 1 lying inside the rectangle
of opposite vertices -1, 1 + 2*i, input:
complexroot(x^3+1,0.1,-1,1+2*i)
Output :
[[-1,1],[[(8+13*i)/16,(4+7*i)/8],1]]




suivant: Exact bounds for real
monter: Exact roots of a
précédent: Exact roots of a
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
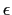 ,
| b1 - b2| <
,
| b1 - b2| < 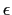 and the root a + ib verifies
a1
and the root a + ib verifies
a1 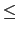 a
a 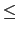 a2 and
b1
a2 and
b1 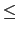 b
b 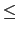 b2.
b2.