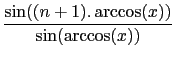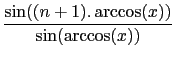Tchebychev polynomial of second kind: tchebyshev2

tchebyshev2 takes as argument an integer n and optionnally a variable name (by default x).
tchebyshev2 returns the Tchebychev polynomial of second kind of degree n.
The Tchebychev polynomial of second kind U(n, x) is defined by:

U(n, x) = $${\frac{{\sin((n+1).\arccos(x))}}{{\sin(\arccos(x))}}}$$

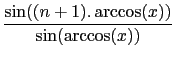
or equivalently:

sin((n + 1)x) = sin(x)*U(n, cos(x))

The U(n, x) verifies the recurrence relation:

U(0, x) = 1,    U(1, x) = 2x,    U(n, x) = 2xU(n - 1, x) - U(n - 2, x)

The polynomials U(n, x) are orthogonal for the scalar product

< f, g > = 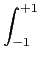$$\int_{{-1}}^{{+1}}$$f (x)g(x)$$\sqrt{{1-x^2}}$$dx

Input :

tchebyshev2(3)

Output :

8*x^3+-4*x

Input :

tchebyshev2(3,y)

Output :

8*y^3+-4*y

Indeed:

sin(4.x) = sin(x)*(8*cos(x)³ -4.cos(x)) = sin(x)*U(3, cos(x))