




suivant: Interpolation with spline functions
monter: Natural splines: spline
précédent: Definition
Table des matières
Index
The set of spline functions of degree l on 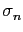 is a
is a
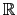 -vectorial subspace of dimension n + l.
-vectorial subspace of dimension n + l.
Proof
On [a, x1], s is a polynomial A of degree less or equal to
l, hence on [a, x1],
s = A(x) = a0 + a1x + ...alxl and A is a linear
combinaison of
1, x,...xl.
On [x1, x2], s is a polynomial B of degree less or equal to
l, hence on [x1, x2],
s = B(x) = b0 + b1x + ...blxl.
s has continuous derivatives up to order l - 1, hence :
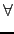
0
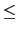 j
j 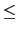 l
l - 1,
B(j)(
x1) -
A(j)(
x1) = 0
therefore
B(x) - A(x) = 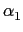 (x - x1)l or
B(x) = A(x) +
(x - x1)l or
B(x) = A(x) + 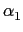 (x - x1)l.
(x - x1)l.
Define the function :
q
1(
x) =
![$\displaystyle \left\{\vphantom{
\begin{array}{rcl}
0 & \mbox{sur} & [a,x_1] \\
(x-x_1)^l & \mbox{sur} & [x_1,b]\\
\end{array}
}\right.$](img275.png)
![$\displaystyle \begin{array}{rcl}
0 & \mbox{sur} & [a,x_1] \\
(x-x_1)^l & \mbox{sur} & [x_1,b]\\
\end{array}$](img276.png)
s|
[a, x2] =
a0 +
a1x + ...
alxl +
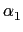 q1
q1(
x)
On [x2, x3], s is a polynomial C of degree less or equal than
l, hence on [x2, x3],
s = C(x) = c0 + c1x + ...clxl.
s has continuous derivatives until l - 1, hence :
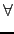
0
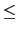 j
j 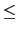 l
l - 1,
C(j)(
x2) -
B(j)(
x2) = 0
therefore
C(x) - B(x) = 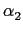 (x - x2)l or
C(x) = B(x) +
(x - x2)l or
C(x) = B(x) + 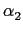 (x - x2)l.
(x - x2)l.
Define the function :
q
2(
x) =
![$\displaystyle \left\{\vphantom{
\begin{array}{rcl}
0 & \mbox{on} & [a,x_2] \\
(x-x_2)^l & \mbox{on} & [x_2,b]\\
\end{array}
}\right.$](img279.png)
![$\displaystyle \begin{array}{rcl}
0 & \mbox{on} & [a,x_2] \\
(x-x_2)^l & \mbox{on} & [x_2,b]\\
\end{array}$](img280.png)
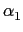 q1(x) +
q1(x) + 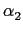 q2(x)
q2(x)
And so on, the functions are defined by :
hence,
s|
[a, b] =
a0 +
a1x + ...
alxl +
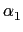 q1
q1(
x) + .... +
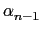 qn-1
qn-1(
x)
and s is a linear combination of n + l independant functions
1, x,..xl, q1,..qn-1.





suivant: Interpolation with spline functions
monter: Natural splines: spline
précédent: Definition
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
![$\displaystyle \begin{array}{rcl}
0 & \mbox{sur} & [a,x_1] \\
(x-x_1)^l & \mbox{sur} & [x_1,b]\\
\end{array}$](img276.png)
![$\displaystyle \begin{array}{rcl}
0 & \mbox{on} & [a,x_2] \\
(x-x_2)^l & \mbox{on} & [x_2,b]\\
\end{array}$](img280.png)
![$\displaystyle \begin{array}{rcl}
0 & \mbox{on} & [a,x_j] \\
(x-x_j)^l & \mbox{on} & [x_j,b]\\
\end{array}$](img282.png)