Compute with the exact root of a polynomial : rootof

Let P and Q be two polynomials given by the list of their coefficients then rootof(P,Q) denotes the value P($\alpha$) where $\alpha$ is the root of Q with largest real part (and largest imaginary part in case of equality).
In exact computations, Xcas will rewrite rational evaluations of rootof as a unique rootof with degree(P) <degree(Q). If the resulting rootof is the solution of a second degree equation, it will be simplified.

Example
Let $\alpha$ be the root with largest imaginary part of Q(x) = x4 + 10x2 + 1 (all roots of Q have real part equal to 0).

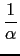• Compute $${\frac{{1}}{{\alpha}}}$$. Input :
  normal(1/rootof([1,0],[1,0,10,0,1]))
  P(x) = x is represented by [1,0] and 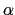$\alpha$ by rootof([1,0],[1,0,10,0,1]).
  Output :
  rootof([[-1,0,-10,0],[1,0,10,0,1]])
  i.e. :
  $${\frac{{1}}{{\alpha}}}$$ = - $$\alpha$$3 - 10$$\alpha$$

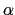• Compute $\alpha$2. Input :
  normal(rootof([1,0],[1,0,10,0,1])^2)
  or (since P(x) = x2 is represented by [1,0,0]) input
  normal(rootof([1,0,0],[1,0,10,0,1]))
  Output :
  -5-2*sqrt(6)