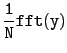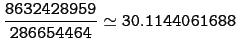suivant: Exponentials and Logarithms
monter: Fourier transformation
précédent: Inverse Fast Fourier Transform
Table des matières
Index
Here are the temperatures T, in Celsius degree, at time t :
| t |
0 |
3 |
6 |
9 |
12 |
15 |
19 |
21 |
| T |
11 |
10 |
17 |
24 |
32 |
26 |
23 |
19 |
What was the temperature at 13h45 ?
Here N = 8 = 2*m. The interpolation polynomial is
p(
t) =
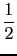 p-m
p-m(exp(- 2
i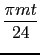
) + exp(2
i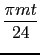
)) +
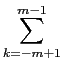 pk
pkexp(2
i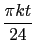
)
and
Input :
q:=1/8*fft([11,10,17,24,32,26,23,19])
Output :
q:=[20.25,-4.48115530061+1.72227182413*i,-0.375+0.875*i,
-0.768844699385+0.222271824132*i,0.5,
-0.768844699385-0.222271824132*i,
-0.375-0.875*i,-4.48115530061-1.72227182413*i]
hence:
- p0 = 20.25
-
p1 = - 4.48115530061 + 1.72227182413*i =
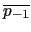 ,
,
-
p2 = 0.375 + 0.875*i =
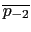 ,
,
-
p3 = - 0.768844699385 + 0.222271824132*i =
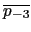 ,
,
-
p-4 = 0.5
Indeed
q = [
q0,...
qN-1] = [
p0,..
p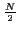 -1
-1,
p-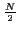
,..,
p-1] =
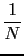 FN
FN([
y0,..
yN-1]) =
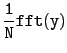
Input :
pp:=[q[4],q[5],q[6],q[7],q[0],q[1],q[2],q[3]]
Here,
pk = pp[k + 4] for k = - 4...3.
It remains to compute the value of the interpolation polynomial at point
t0 = 13, 75 = 55/4, Input
t0(j):=exp(2*i*pi*(13+3/4)/24*j)
T0:=1/2*pp[0]*(t0(4)+t0(-4))+sum(pp[j+4]*t0(j),j,-3,3)
evalf(re(T0))
Output :
29.4863181684
The temperature is predicted to be equal to 29.49 Celsius degrees.
Input :
q1:=[q[4]/2,q[3],q[2],q[1],q[0]/2]
a:=t0(1) (ou a:=-exp(i*pi*7/48))
g(x):=r2e(q1,x)
evalf(2*re(g(a)))
or
2.0*re(q[0]/2+q[1]*t0(1)+q[2]*t0(2)+q[3]*t0(3)+q[4]/2*t0(4))
Output :
29.4863181684
Remark
Using the Lagrange interpolation polynomial (the polynomial is not periodic),
input :
l1:=[0,3,6,9,12,15,18,21]
l2:=[11,10,17,24,32,26,23,19]
subst(lagrange(l1,l2,13+3/4),x=13+3/4)
Output :
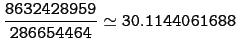





suivant: Exponentials and Logarithms
monter: Fourier transformation
précédent: Inverse Fast Fourier Transform
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
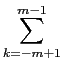 pkexp(2i
pkexp(2i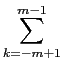 pkexp(2i
pkexp(2i