Find the Fourier coefficients cn of the periodic function f of
period 2.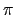 and defined on [0;2.
and defined on [0;2.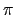 [ by f (x) = x2.
[ by f (x) = x2.
Input :
assume(n,integer)
fourier_cn(x^2,x,2*pi,n)
Output :
((2*i)*pi*n+2)/n^2
If you don't specify assume(n,integer), the output will not be
simplified :
((2*i)*pi^2*n^2*exp((-i)*n*2*pi)+2*pi*n*exp((-i)*n*2*pi)+
(-i)*exp((-i)*n*2*pi)+i)/(pi*n^3)
You might simplify this expression by replacing
exp((-i)*n*2*pi) by 1, input :
subst(ans(),exp((-i)*n*2*pi)=1)
Output :
((2*i)*pi^2*n^2+2*pi*n+-i+i)/pi/n^3
This expression is then simplified with normal, the final
output is :
((2*i)*pi*n+2)/n^2
Hence for n 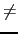 0,
cn =
0,
cn = 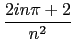 .
As shown in this example, it is better to input assume(n,integer) before calling fourier_cn.
.
As shown in this example, it is better to input assume(n,integer) before calling fourier_cn.
We must also compute cn for n = 0, input :
fourier_cn(x^2,x,2*pi,0)
Output :
4*pi^2/3
Hence for n = 0,
c0 = 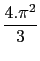 .
.
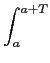 f (x)e
f (x)e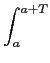 f (x)e
f (x)e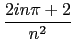 .
As shown in this example, it is better to input assume(n,integer) before calling fourier_cn.
.
As shown in this example, it is better to input assume(n,integer) before calling fourier_cn.