ibpdv

ibpdv is used to search the primitive of an expression written as u(x).v'(x).
ibpdv takes two arguments :

• an expression u(x).v'(x) and v(x) (or a list of two expressions [F(x), u(x)*v'(x)] and v(x)),
• or an expression g(x) and 0 (or a list of two expressions [F(x), g(x)] and 0).

ibpdv returns :

• if v(x) 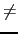$\neq$ 0, the list [u(x).v(x), - v(x).u'(x)] (or [F(x) + u(x).v(x), - v(x).u'(x)]),
• if the second argument is zero, a primitive of the first argument g(x) (or F(x)+a primitive of g(x)) :
  hence, ibpdv(g(x),0) returns a primitive G(x) of g(x) or
  ibpdv([F(x),g(x)],0) returns F(x)+G(x) where diff(G(x))=g(x).

Hence, ibpdv returns the terms computed in an integration by parts, with the possibility of doing several ibpdv succesively.
When the answer of ibpdv(u(x)*v'(x),v(x)) is computed, to obtain a primitive of u(x).v'(x), it remains to compute the integral of the second term of this answer and then, to sum this integral with the first term of this answer : to do this, just use ibpdv command with the answer as first argument and a new v(x) (or 0 to terminate the integration) as second argument.
Input :

ibpdv(ln(x),x)

Output :

[x.ln(x),-1]

then

ibpdv([x.ln(x),-1],0)

Output :

-x+x.ln(x)

Remark
When the first argument of ibpdv is a list of two elements, ibpdv works only on the last element of this list and adds the integrated term to the first element of this list. (therefore it is possible to do several ibpdv successively).
For example :
ibpdv((log(x))^2,x) = [x*(log(x))^2,-(2*log(x))]
it remains to integrate -(2*log(x)), the input :
ibpdv(ans(),x) or input :
ibpdv([x*(log(x))^2,-(2*log(x))],x)
Output :
[x*(log(x))^2+x*(-(2*log(x))),2]
and it remains to integrate 2, hence input ibpdv(ans(),0) or
ibpdv([x*(log(x))^2+x*(-(2*log(x))),2],0).
Output : x*(log(x))^2+x*(-(2*log(x)))+2*x