




suivant: Integration by parts :
monter: Integration
précédent: Discrete summation: sum
Table des matières
Index
Riemann sum : sum_riemann
sum_riemann takes two arguments : an expression depending of
two variables and the list of the name of these two variables.
sum_riemann(expression(n,k),[n,k]) returns in the neighboorhoud of
n = + 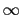 an equivalent of
an equivalent of
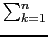 expression(n, k) (or of
expression(n, k) (or of
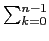 expression(n, k) or of
expression(n, k) or of
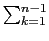 expression(n, k))
when the sum is looked as a Riemann sum associated to a continue
function defined on [0,1] or returns
"it is probably not a Riemann sum" when the resarch is unavailing.
expression(n, k))
when the sum is looked as a Riemann sum associated to a continue
function defined on [0,1] or returns
"it is probably not a Riemann sum" when the resarch is unavailing.
Exercise 1
Suppose
Sn = 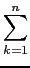
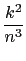 .
.
Compute
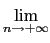 Sn.
Sn.
Input :
sum_riemann(k^2/n^3,[n,k])
Output :
1/3
Exercise 2
Suppose
Sn = 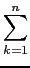
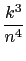 .
.
Compute
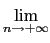 Sn.
Sn.
Input :
sum_riemann(k^3/n^4,[n,k])
Output :
1/4
Exercise 3
Compute
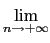 (
(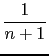 +
+ 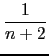 + ... +
+ ... + 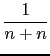 ).
).
Input :
sum_riemann(1/(n+k),[n,k])
Output :
log(2)
Exercise 4
Suppose
Sn = 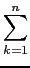
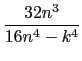 .
.
Compute
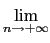 Sn.
Sn.
Input :
sum_riemann(32*n^3/(16*n^4-k^4),[n,k])
Output :
2*atan(1/2)+log(3)
giac documentation written by Renée De Graeve and Bernard Parisse
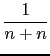 ).
).
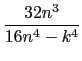 .
.