




suivant: Discrete summation: sum
monter: Integration
précédent: Integration
Table des matières
Index
Antiderivative and definite integral : integrate int Int
integrate (or int) compute the primitive
or a definite integral. A difference between the two
commands is that, if you input quest(), just after the evaluation of
integrate, the answer is written with the 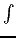 symbol.
symbol.
integrate (or int or Int) takes one, two or four arguments.
Int is the inert form of integrate, it prevents evaluation
for example to avoid a symbolic computation that might not be
successfull if you just want a numeric
evaluation.
Input :
evalf(Int(exp(x^2),x,0,1))
Or :
evalf(int(exp(x^2),x,0,1))
Output :
1.46265174591
Exercise 1
Let
f (
x) =
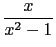
+ ln(
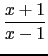
)
Find a primitive of f.
Input :
int(x/(x^2-1)+ln((x+1)/(x-1)))
Output :
x*log((x+1)/(x-1))+log(x^2-1)+1/2*log(2*x^2/2-1)
Or define the function f, input :
f(x):=x/(x^2-1)+ln((x+1)/(x-1))
then input :
int(f(x))
Output of course the same result.
Warning
For Xcas, log is the natural logarithm (like ln),
as log10 is 10-basis logarithm
Exercise 2
Compute :
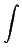
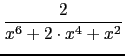 dx
dx
Input :
int(2/(x^6+2*x^4+x^2))
Output :
2*((3*x^2+2)/(-(2*(x^3+x)))+-3/2*atan(x))
Exercise 3
Compute :
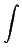
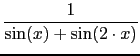 dx
dx
Input :
integrate(1/(sin(x)+sin(2*x )))
Output :
(1/-3*log((tan(x/2))^2-3)+1/12*log((tan(x/2))^2))*2





suivant: Discrete summation: sum
monter: Integration
précédent: Integration
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
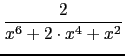 dx
dx
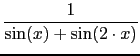 dx
dx