




suivant: Top and leaves of
monter: Functions and expressions with
précédent: Difference between function and
Table des matières
Index
Transform an expression into a fonction : unapply
unapply is used to transform an expression into a function.
unapply takes two arguments an expression and the name of a variable.
unapply returns the function defined by this expression and
this variable.
Warning when a function is defined,
the right member of the affectation is not evaluated,
hence g:=sin(x+1); f(x):=g does not defined the function
f : x 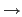 sin(x + 1) but defines the function
f : x
sin(x + 1) but defines the function
f : x 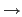 g. To defined the former function, unapply
should be used, like in the following example:
g. To defined the former function, unapply
should be used, like in the following example:
Input :
g:= sin(x+1); f:=unapply(g,x)
Output :
(sin(x+1), (x)->sin(x+1))
hence, the variable g is assigned to a symbolic expression
and the variable f is assigned to a function.
Input :
unapply(exp(x+2),x)
Output :
(x)->exp(x+2)
Input :
f:=unapply(lagrange([1,2,3],[4,8,12]),x)
Output :
(x)->4+4*(x-1)
Input :
f:=unapply(integrate(log(t),t,1,x),x)
Output :
(x)->x*log(x)-x+1
Input :
f:=unapply(integrate(log(t),t,1,x),x)
f(x)
Output :
x*log(x)-x+1
Remark
Suppose that f is a function of 2 variables
f : (x, w) 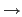 f (x, w),
and that g is the function defined by
g : w
f (x, w),
and that g is the function defined by
g : w 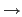 hw where hw is the function defined by
hw(x) = f (x, w).
hw where hw is the function defined by
hw(x) = f (x, w).
unapply is also used to define g with Xcas.
Input :
f(x,w):=2*x+w
g(w):=unapply(f(x,w),x)
g(3)
Output :
x->2 . x+3





suivant: Top and leaves of
monter: Functions and expressions with
précédent: Difference between function and
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
![]() sin(x + 1) but defines the function
f : x
sin(x + 1) but defines the function
f : x ![]() g. To defined the former function, unapply
should be used, like in the following example:
g. To defined the former function, unapply
should be used, like in the following example: