




suivant: Simplify : simplify
monter: Algebraic expressions
précédent: Complex zeros of an
Table des matières
Index
Normal form : normal
normal takes as argument an expression.
The expression is considered as a rational fraction with respect
to generalized identifiers
(either true identifiers or transcendental functions replaced by
a temporary identifiers) with coefficients in 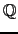 or
or
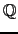 [i]
or in an algebraic extension (e.g.
[i]
or in an algebraic extension (e.g.
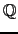 [
[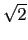 ]).
normal returns the expanded irreducible representation
of this rational fraction. See also ratnormal for pure rational
fractions or simplify if the transcendental functions are
not algebraically independant.
]).
normal returns the expanded irreducible representation
of this rational fraction. See also ratnormal for pure rational
fractions or simplify if the transcendental functions are
not algebraically independant.
Input :
normal((x-1)*(x+1))
Output :
x^2-1
Remarks
- Unlike simplify,
normal does not try to find algebraic relations between
transcendental functions like
cos(x)2 + sin(x)2 = 1.
- It is sometimes necessary to run the normal command twice to
get a fully irreducible representation of an expression
containing algebraic extensions.
giac documentation written by Renée De Graeve and Bernard Parisse