Sujets du capes 2010 avec XcasRenee.Degraeve@wanadoo.frDécembre 2010 |
Table des matières
1 Thème : Étude de suites
1.1 L’exercice
Soit a un réel. On considère la suite (un )n∈ ℕ définie par
u0 = a et, pour tout entier n :
-
Étudier les cas a = 0, a = 1 et a = 2.
Dans toute la suite, on suppose que a∈ ]0; 1[.
- Étudier les variations de la fonction f définie sur [0; 1] par :
f(x)=x(2−x).
- Montrer que, pour tout entier n, on a : 0 ≤ un ≤ un+1 ≤ 1.
- Montrer que la suite (un )n∈ ℕ est convergente et déterminer
sa limite.
1.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en totalité
lors de l’entretien avec le jury.
Le candidat présentera au Jury :
les méthodes et les savoirs mis en jeu dans l’exercice ;
Le candidat rédigera sur ses fiches :
sa réponse à la question 4) ;
un ou plusieurs exercices se rapportant au thème "Étude de suites".
1.3 Solution de l’exercice avec Xcas
-
pour a=0 u1=0 et pour tout n ∈ ℕ un=0,
pour a=1 u1=1 et pour tout n∈ ℕ un=1,
pour a=2 u1=0 et pour tout n∈ ℕ un=0,
- Pour étudier la fonction f, on tape :
f(x):=(x*(2-x)
f1:=function_diff(f)
normal(f1(x))
On obtient :
-2*x+2
Donc f admet un maximum en x=1 qui vaut 1.
Pour x<1, f est croissante et pour x>1, f est décroissante.
f(x)=0 pour x=0 et x=2 donc pour x ∈[0;2] on a 0≤ f(x) ≤ 1.
Pour faire le graphe de f sur [0;2], on tape :
plotfunc(f(x),x=0..2)
Pour pouvoir faire bouger a entre 0 et 1 et voir le graphe
de f(x)=x(2−x) pour x∈ [0;2] et les 6 premiers termes de un , on tape
dans un niveau de géométrie:
supposons(a=[0.3,0,1,0.1]);
plotseq(x*(2-x),[a,0,2],6)
On obtient :

- Puisque pour x ∈[0;2] on a 0≤ f(x) ≤ 1 et que
un+1=f(un) :
pour tout n>0 et pour tout a ∈ [0; 2], on a : 0≤ un ≤ 1.
Pour avoir le signe de un+1−un=f(un)−un, on tape :
factor(x*(2-x)-x)
On obtient :
-x*(x-1)
Puisque pour tout n>0, 0≤ un ≤ 1, on en déduit que
un+1−un≤ 0.
si on suppose a∈ ]0;1[ pour tout n≥ 0, on a
0≤ un≤ un+1≤ 1
La suite u est donc croissante et majorée donc u est convergente.
Sa limite l vérfie l=l(2−l) et l≥ a>0 donc l=1
2 Thème : Probabilités
2.1 L’exercice
Une urne contient une boule blanche et une boule noire. On effectue
au hasard n tirages successifs (n ≥ 2) d’une boule en remettant la
boule dans l’urne après chaque tirage.
-
a) Calculer la probabilité de l’événement "toutes les boules
tirées ont la même couleur".
1 b) Calculer la probabilité de l’événement "on obtient exactement
une boule blanche ".
On considère les deux événements A et B suivants :
A : "on obtient des boules des deux couleurs"
B : "on obtient au plus une boule blanche"
- Calculer les probabilités P(A∩ B), P(A) et P(B).
- Montrer que P (A∩ B) = P(A) × P(B) si et seulement si l’entier
n vérifie l’égalité 2n−1= n+1.
- En déduire qu’il existe une valeur unique de n pour laquelle A et
B sont deux événements indépendants (on pourra considérer la suite
(un )n≥ 2 définie par un =2n−1−(n+1) et montrer qu’elle est
strictement croissante).
2.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat présentera au Jury :
les méthodes et les savoirs mis en jeu dans l’exercice ;
sa réponse à la question 1)
Le candidat rédigera sur ses fiches :
la réponse á la question 2) ;
un ou plusieurs exercices se rapportant au thème "Probabilités".
2.3 Solution de l’exercice avec Xcas
-
a) "toutes les boules tirées ont la même couleur"
La probabilité d’avoir n boules noires (resp blanches) est 1/2n donc
La probabilité d’avoir n boules de la même couleur" est 2/2n=1/2n−11 b) "on obtient exactement une boule blanche "
La boule blanche peut être tirée soit au 1ier, soit au 2ième,... soit au
nième coup. Donc la probabilité d’avoir exactement une boule blanche est
n/2n
- Soient A : "on obtient des boules des deux couleurs"
B : "on obtient au plus une boule blanche"
A∩ B est l’événement "on obtient exactement une boule blanche "
donc P(A∩ B)=n/2n.
non A est l’événement "toutes les boules tirées ont la même couleur"
donc P(A)=1−1/2n−1
B est l’événement "toutes les boules tirées sont noires" union
"on obtient exactement une boule blanche " donc P(B)=1/2n+n/2n
- On a :
P (A∩ B) = P(A) × P(B) <=>
n/2n=(1−1/2n−1)*(1/2n+n/2n) <=>
n=(1−1/2n−1)*(1+n)=1+n−1/2n−1)*(1+n) <=>
1/2n−1)*(1+n)=1 <=>
2n−1)=(1+n)
- Soit un=2n−1−(n+1) pour n≥ 2
un+1−un=2n−(n+2)−2n−1+(n+1)=2n−1−1 puisque n≥ 2 on a
2n−1−1≥ 2−1=1>0 donc u est strictement croissante.
pour n=2 on a u2=−1, u3=0 puis un>0 pour n>4
Donc il existe une valeur unique de n pour laquelle A et
B sont deux événements indépendants et ette valeur est n=3
3 Thème : Équations différentielles
3.1 L’exercice
Le plan est rapporté à un repère orthonormal.
-
Soit C la courbe représentative de la fonction
exponentielle x −> ex.
Pour tout point M d’abscisse t appartenant à C,
on considère le point P de coordonnées (t, 0) et le point N, point
d’intersection de la tangente en M à C avec l’axe des abscisses. Montrer
que la distance PN est constante.
- Dans la suite de l’exercice f désigne une fonction définie sur
ℝ, strictement positive, dérivable et dont la fonction dérivée est
strictement positive. Pour tout point M d’abscisse t appartenant à la
courbe représentative de f , on considère le point P de coordonnées
(t,0) et le point N , point d’intersection de la tangente en M à la
courbe représentative de f avec l’axe des abscisses.
2.a) Calculer la distance PN en fonction de f(t) et de f′(t).
2.b) Déterminer une équation différentielle (Ek) vérifiée par
les fonctions f définies sur ℝ, strictement positives, dérivables et
dont la fonction dérivée est strictement positive, pour lesquelles la
distance PN est une constante k.
2.c) Déterminer les fonctions f solutions de (Ek).
3.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury
Le candidat présentera au Jury :
les méthodes et les savoirs mis en jeu dans l’exercice ;
sa réponse à la question 2).
Le candidat rédigera sur ses fiches :
un ou plusieurs exercices se rapportant au thème
"Équations différentielles".
3.3 Solution de l’exercice avec Xcas
-
La longueur PN est constante.
On tape :
C:=plotfunc(exp(x));
assume(t=[2,-5,5,0.1]);
M:=point(t,exp(t));
P:=point(t);
T:=tangente(C,M);
N:=inter_unique(T,droite(y=0));
normal(longueur(P,N));
On obtient :

L’équation de T : droite(y=(-t*exp(t)+exp(t)+exp(t)*x))
Le point N est : point(t-1)
La longueur de PN : 1
On a en effet si f(t)=exp(t):
T a pour pente f′(t)=exp(t) et passe par le point M=(t;f(t) et son
équation est donc : y=f′(t)*(x−t)+f(t)=exp(t)*(x−t+1)
N est donc le point (t−1;0)
La longueur de PN vaut donc |t−(t−1)|=1
- On a :
T a pour équation : y=f′(t)*(x−t)+f(t),
N est donc le point (t−f(t)/f′(t);0) (car f′(t)≠ 0)
La longueur de PN vaut donc |t−(t−f(t)/f′(t))|=f(t)/f′(t) car
f(t)/f′(t)>0
L’équation Ek est donc :
(Ek) f(t)/f′(t)=k soit l’équation différentielle ky′=y
Pour résoudre cette équation on a :
si k=0 alors y(t)=0
Si k≠ 0 alors y′=y/k donc y(t)=c*exp(t/k).
Avec Xcas, on tape :
desolve(k*y’=y) et on obtient c_0*exp(x/k)
ou on tape :
desolve(k*diff(y,t)=y, [t,y]) et on obtient c_0*exp(t/k)
4 Thème : Calcul de grandeurs : longueurs, aires, volumes
4.1 L’exercice
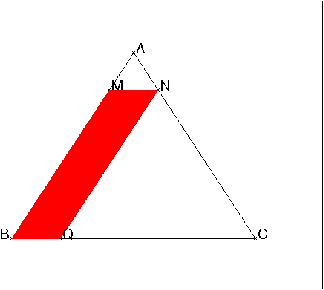
Soit ABC un triangle isocèle en A tel que AC = 5 et BC = 6. Un
point M se déplace sur le segment [AB] en restant différent des points
A et B. Le point N est l’intersection de (AC) et de la parallèle à
(BC) passant par M. On désigne par Q le point du segment [BC]
tel que le quadrilatère MNQB soit un parallélogramme. On se propose de
déterminer la position du point M sur le segment [AB] pour que l’aire du
parallélogramme MNQB soit maximale. Pour cela on pose AM = x et on note
f(x) l’aire du parallélogramme MNQB.
-
Montrer que MN=6/5x et en déduire l’aire du triangle
AMN.
- Montrer que QC=6/5(5−x) et en déduire l’aire du triangle
CNQ.
- Montrer que f(x)=12/25(−2x2+10x).
- Déterminer la valeur de x pour laquelle f(x) est maximale.
4.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat présentera au jury :
Les méthodes et les savoirs mis en jeu dans la résolution de
l’exercice ;
un énoncé à présenter en classe de Seconde pour résoudre la
question 4) de l’exercice.
Le candidat rédigera sur ses fiches :
sa réponse à la question 1).
un ou plusieurs exercices se rapportant au thème : "Calcul de
grandeurs : longueurs, aires, volumes".
4.3 Solution de l’exercice sans Xcas
4.3.1 Réponses aux différentes questions
-
0n calcule la hauteur hA du triancle ABC.
On a d’après Pythagore :
hA2=52−32=16 donc hA=4.
Les triangles AMN et ABC sont semblables donc
AM/AB=MN/BC
Donc MN=BCAM/BA=6x/5.
La hauteur h du triangle AMN issue de A a pour longueur :
h=√x2−MN2/4=√x2−9x2/25=4x/5
L’aire du triangle AMN est donc 4x/5*3x/5=12x2/25
On peut aussi dire que l’aire du triangle ABC vaut 4*6/2=12
Les triangles AMN et ABC sont homothétiques de rapport
k=AM/AB=x/5
Donc l’aire du triangle AMN est k2*12=12*(x/5)2=12x2/25
- Les triangles NQC et ABC sont semblables de rapport
NQ/AB=QC/BC=5−x/5
Donc QC=BCNQ/BA=6(5−x)/5
L’aire du triangle NQC est donc 12*((5−x)/5)2
- L’aire du parallélogramme MNQB s’obtient en enlevant à l’aire de
ABC l’aire des 2 triangles précédents :
f(x) vaut donc :
12−12x2/25−12*((5−x)/5)2=12/25(25−x2−(x2+25−10x)
On peut aussi dire que l’aire de NMBQ est égale à :
MN(hA−h)=6x/5(4−4x/5=24x/25(5−x)
- Donc :
f(x)=12/25(−2x2+10x)
On a f′(x)=12/25(−4x+10) donc d’apres le signe de f′(x), la valeur
de x pour laquelle f(x) est maximale est x=5/2 et M est alors le milieu
de AC. Ce maximum vaut 6 soit la moitié de l’aire du triangle ABC.
4.3.2 Solution de l’exercice en analytique
On pose BM=x.
On choisit comme repère : OCA avec O le milieu de BC.
On a : A=(0;4),B=(−3;0),C=(3;0)
Pour avoir l’aire du parallélogramme MNQB il suffit de connaitre la
longueur de MN et l’ordonnée de M.
Les triangles AMN et ABC sont semblables donc
AM/AB=MN/BC
.
Donc MN=BCAM/BA=6x/5.
La droite (A,B) a pour équation : y=4x/3+4
M a pour abscisse −3x/5 donc pour ordonnèe −4x/5+4.
L’aire du parallélogramme MNQB est donc :
4−x+5/56x/5=12/25(−2x2+10x
Remarque
Pour montrer que l’aire du parallélogramme MNQB est maximale lorsque MN
passe par les milieux de AB et de AC, il est plus judicieux de prendre
comme paramètre l’ordonnée de M et d’utiliser un repère d’origine B
et de prendre BC comme axe des x.
4.3.3 Réponses aux différentes questions avec Xcas
Avec Xcas on a la possibilité de définir paramètre formel x
en mettant par exemple dans un niveau de géométrie :
assume(x=[1,0,5,0.1]);
Cela permet de faire la figure avec x=1, de faire apparaitre un curseur qui
permet de changer cette valeur entre 0 et 5 avec un pas de 0.1 et surtout de
faire faire à Xcas les calculs en fonction du paramètre formel x.
On ouvre un niveau de géométrie et on tape :
B:=point(-3,affichage=quadrant2);
C:=point(3);
A:=point(4*i);
triangle(A,B,C);
assume(x=[1,0,5,0.1]);
M:=point(4*i+x/5*(B-A));
N:=point(4*i+x/5*(C-A));
p:=parallelogramme(N,M,B,Q,affichage=1+rempli):;p;
legende(Q,"Q",quadrant2);
f:=unapply(aire(N,M,B,Q),x);
plotfunc(f(x),x=0..5,affichage=4+epaisseur_ligne_2);
M0:=point(x+i*f(x),affichage=4+epaisseur_point_2);
On obtient sur le même écran la figure, le graphe de f(x) et sur ce
graphe le point de coordonnées (x;f(x).

On peut ainsi voir évoluer la figure en fonction du paramètre x et
observer : pour cela on fait bouger le curseur x pour voir le point M
se déplacer sur AB et le point M0 d’abscisse x et d’ordonnée f(x)
(i.e. l’aire de NMBQ), se déplacer sur le graphe de f.
Puis, on fait faire le calcul à Xcas.
On tape normal(longueur(M,N),aire(A,M,N))
On obtient (6*x)/5,12/25*x^2
On tape normal(longueur(Q,C),aire(Q,C,N))
On obtient (-6*x+30)/5, 12/25*x^2-24/5*x+12
On tape f1:=function_diff(f)
On obtient (‘ x‘)->-(24*2*‘ x‘)/25+24/5
On tape solve(f1(x)=0 et on obtient 5/2
On tape f(5/2) et on obtient 6
4.4 Solution géométrique de l’exercice avec Xcas
Xcas sert ici à faire la figure et faire évoluer les paramètres
pour l’observation et le contrôle des conclusions.
Pour faire la figure on tape (Si O est le milieu de BC, alors AO=4):
On donne à M une autre position M1 et on regarde comment les aires des
parallélogrammes MNQB et M1N1Q1B évoluent.
B:=point(-3,affichage=quadrant2);
C:=point(3);
A:=point(4*i);
triangle(A,B,C);
assume(x=[1,0,5,0.1]);
M:=point(4*i+x/5*(B-A));
N:=point(4*i+x/5*(C-A));
p:=parallelogramme(N,M,B,Q,affichage=1+rempli):;
p;
supposons(x1=[3.8,0,5,0.1]);
M1:=point(4*(i)+x1/5*(B-A));
N1:=point(4*i+x1/5*(C-A));
parallelogramme(N1,M1,B,Q1,affichage=2+rempli);
legende(Q,"Q",quadrant2);
I:=inter_unique(droite(M1,N1),droite(N,Q));
parallelogramme(Q,Q1,N1,I,affichage=4+rempli);
Q2:=translation(N-N1,Q1);
C2:=translation(N-N1,C)
segment(Q2,C2);
segment(Q2,Q1);
segment(-1.5+2*i,1.5+2*i,affichage=3+ligne_tiret);

On remarque que :
-
Les triangles AMN et NQC sont semblables à ABC
- Si M et M1 sont symétriques par rapport au milieu de AB
alors les parallélogrammes MNQB et M1N1Q1B ont même aire. En effet
les triangles AMN et N1Q1C sont égaux ainsi que les triangles
AM1N1 et NQC donc ont même aire. La fonction f(x) ègale à l’aire
du parallélogramme MNQB est donc symétrique par rapport à la droite
x=AB/2
- On suppose alors x<x1<AB/2 donc MN<M1N1<BC/2.
l’aire de MNQB est composée de l’aire rouge et de l’aire verte
l’aire de M1N1Q1B est composée de l’aire verte et de l’aire bleue
On va comparer l’aire rouge et l’aire bleue :
On fait effectuer au triangle N1Q1C,
une translation de vecteur N1N : N1 se transforme en N,
Q1 se transforme en Q2, C se transforme en C2, Donc les triangles
N1Q1C et NQ2C2. De plus les triangles NIN1 et Q2QQ1 sont égaux et
cela a pour conséquence que les parallélogrammes QQ1N1I et CC2Q2Q1 ont
même aire. Pour vérifier on peut taper :
aire(Q1,C,C2,Q2)==aire(Q,Q1,N1,I) et obtenir 1.
On a : Q1C=BC−BQ1=BC−M1N1 et M1N1<BC/2 donc Q1C>BC/2>MN.
On en déduit que l’aire bleue est plus grande que l’aire rouge c’est à dire
que lorsque x croit de 0 à AB/2 la fonction est croissante et que par
symétrie lorsque x croit de BC/2 à BC la fonction décroit.
Le maximum est atteint pour x=AB/2 et vaut la moitié de l’aire de ABC.
Cela est général et ne dépend pas de la forme du triangle ABC
4.5 L’exercice avec un triangle ABC rectangle en B ou quelconque
-
Soit un triangle ABC rectangle en B. Un point M se déplace sur le
segment [AB] en restant différent des points
A et B. Le point N est l’intersection de (AC) et de la parallèle à
(BC) passant par M. On désigne par Q le point du segment [BC]
tel que le quadrilatère MNQB soit un rectangle. On se propose de
déterminer la position du point M sur le segment [AB] pour que l’aire du
rectangle MNQB soit maximale.
- Soit un triangle ABC quelconque. Un point M se déplace sur le
segment [AB] en restant différent des points
A et B. Le point N est l’intersection de (AC) et de la parallèle à
(BC) passant par M. On désigne par Q le point du segment [BC]
tel que le quadrilatère MNQB soit un parallélogramme. On se propose de
déterminer la position du point M sur le segment [AB] pour que l’aire du
parallélogramme MNQB soit maximale.
Soit un triangle ABC rectangle en B et un triangle A1B1C1 quelconque.
On définit le point D pour que ABCD soit un rectangle et le point
D1 pour que A1B1C1D1 soit un parallélogramme.
On fait les 2 figures suivantes en posant yM=t, pour cela on tape par
exemple :
A:=point(-3,5);
B:=point(-3,'affichage'=quadrant2);
C:=point(0,'affichage'=quadrant2);
O:=milieu(A,C);
triangle(A,B,C);
supposons(t=[3.1,0,5,0.1]);
M:=point(-3+t*(i),'affichage'=quadrant2);
N:=point(-3*t/5+i*t,affichage=quadrant2);;
Q:=point(-3t/5);
quadrilatere(N,M,B,Q,affichage=1+ rempli);
quadrilatere(N,P,D,R,affichage=4+ rempli);
P:=point(i*t);
R:=point(-3t/5)+i*5);
D:=point(5i);
triangle(A,D,C);
A1:=point(2,5);
B1:=point(1,'affichage'=quadrant2);
C1:=point(4);
D1:=point(5+5i);
M1:=point(1+t/5+t*(i),'affichage'=quadrant2);
P1:=point(4+t/5+t*(i));
O1:=milieu(A1,C1);
triangle(A1,B1,C1);
N1:=point(4-2*t/5+t*(i),'affichage'=quadrant2);
Q1:=point(4-3t/5);
triangle(A1,D1,C1);
R1:=point(5-3t/5+5i);
quadrilatere(N1,M1,B1,Q1,affichage=1+ rempli);
quadrilatere(N1,P1,D1,R1,affichage=4+ rempli);
segment(-3+(5-t)*i, -3+3t/5+(5-t)*i);
segment(-3+3t/5, -3+3t/5+(5-t)*i);
segment(1+(5-t)/5+(5-t)*i, 1+(5+2t)/5+(5-t)*i);
segment(1+(3t)/5, 1+(5+2t)/5+(5-t)*i);
On obtient :
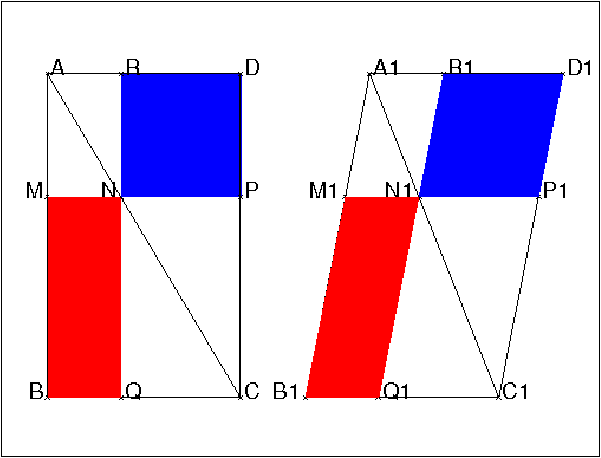
On peut faire bouger le paramètre t.
On démontre facilement que les aires rouges sont égales entre elles et que
chaque aire rouge et aussi égale à une aire bleue.
Dans chacune des figures :
l’aire rouge est l’aire qui correspond à la position
de M d’ordonnée t et l’aire bleue est l’aire qui correspond à la
position de M d’ordonnée yA−t.
Le graphe de l’aire f(t) du quadrilatère NMBQ (resp N1M1B1Q1) admet
donc un axe de symétrie en t=yA/2
4.5.3 Solution géométrique
On se raméne à un triangle rectangle en B de même aire et
on met sur la même figure deux positions de M pour t<b<yA/2, et on
compare les aires corespondantes à ces 2 positions. Pour cela on tape :
A:=point(-3,5);
B:=point(-3,'affichage'=quadrant2);
C:=point(0);
O:=milieu(A,C);
triangle(A,B,C);
supposons(t=[1.3,0,2.5,0.1]);
M:=point(-3+t*(i),'affichage'=quadrant2);
N:=point(-3*t/5+i*t,affichage=quadrant2);;
Q:=point(-3t/5);
quadrilatere(N,M,B,Q,affichage=1+ rempli);
D:=point(5i);
triangle(A,D,C);
P:=point(i*t);
supposons(b=[2,t,2.5,0.1]);
quadrilatere(-3+b*i,-3*b/5+b*i,-3*b/5,-3,affichage=2+ rempli);
quadrilatere(-3+t*i,-3*b/5+t*i,-3*b/5,-3,affichage=3+ rempli);
quadrilatere(-3*t/5+i*b,b*i,P,N,affichage=4+ rempli);
segment(-3*b/5+b*i,-3*t/5+i*b);
On obtient :
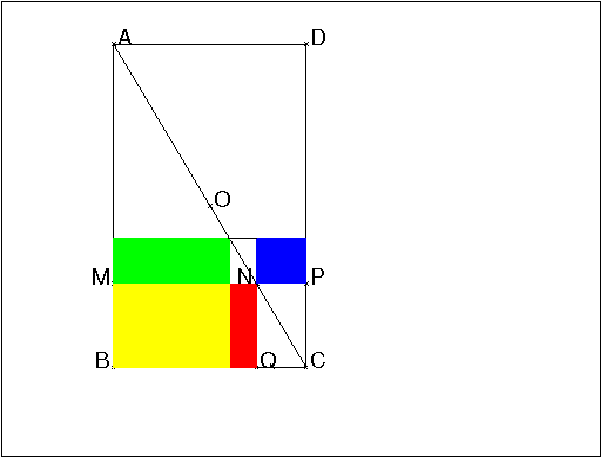
Quand t augmente de 0 à yA/2, l’aire du quadrilatère NMBQ passe de :
l’aire jaune+l’aire rouge à l’aire jaune+l’aire verte.
D’après le lemme, on a : aire rouge =aire bleue.
L’aire bleue est inférieure à l’aire verte car t<yA/2.
Donc le graphe de l’aire du quadrilatère NMBQ (resp N1M1B1Q1) est
croissante sur 0;yA/2
4.5.4 Solution en analytique avec un triangle ABC rectangle en B
On prend comme repère BCA. La droite (A,C) de pente m<0 a comme
équation : y=mx+xA.
Soit M de coordonnées (0;t) un point de la droite AB.
Les coordonnées du point N vérifie donc yN=t=m*xN+xA) et
le rectangle NMBQ a comme aire : xN*yN=xN*(m*xN+xA).
xN*(m*xN+xA) est un trinôme du 2nd degré en xN qui a comme maximum
xA/2 atteint en xN=−xA/(2m) (car m<0).
L’aire du rectangle NMBQ est donc maximum pour t=yN=xA/2 i.e. lorsque M est le milieu de AB.
5 Thème : Arithmétique
5.1 L’exercice
Pour tout entier n≥ 1 on pose an = 1! + 2! +...+ n!
On donne la décomposition en facteurs premiers des dix premiers termes de
la suite (an ) :
a1 = 1
a2 = 3
a3 = 32
a4 = 3 × 11
a5 = 32 × 17
a6 = 32 × 97
a7 = 34 × 73
a8 = 32 × 11 × 467
a9 = 32 × 131 × 347
a10 = 32 × 11 × 40787
-
Montrer que an n’est jamais divisible par 2, par 5 ni par 7.
- Peut-on affirmer que an est divisible par 11 á partir d’un certain
rang ?
- Peut-on affirmer que, à partir d’un certain rang, an est divisible
par 32 mais pas par 33 ?
5.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse à la question 3) ;
un ou plusieurs exercices se rapportant au thème « Arithmétique ».
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
5.3 Solution de l’exercice sans Xcas
On pose : an = 1! + 2! +...+ n! pour n≥ 1
Pour avoir, avec Xcas, la décomposition en facteurs premiers de
a10, on tape : ifactor(sum(p!,p=1..10)) et
pour avoir la liste des décompositions en facteurs premiers de a1..a10,
on tape : ifactor(sum(p!,p=1..n))$(n=1..10) et on obtient :
1,3,3^2,3*11,3^2*17,3^2*97,3^4*73,3^2*11*467, 3^2*131*347, 3^2*11*40787
-
an n’est jamais divisible par 2, par 5 ni par 7
-
an n’est jamais divisible par 2. En effet ∑p=2np! est un
nombre pair puisque p! est divisible par 2 lorsque p≥ 2.
Donc an=1+∑p=2np! est un nombre impair.
Donc an n’est jamais divisible par 2.
- an n’est jamais divisible par 5. En effet p! est
divisible par 5 lorsque p≥ 5.
Donc an−a4=∑p=5np! est divisible par 5.
a1 = 1, a2 = 3, a3 = 322 et a4 = 3 × 11 ne sont pas divisble par 5 et donc an n’est pas divisible par 5 lorsque n<5.
an=a4+∑p=5np! : a4 n’est pas divisible par 5
et ∑p=5np! est divisible par 5 donc an n’est pas divisible par 5
lorsque n≥ 5.
Donc an n’est jamais divisible par 5.
- an n’est jamais divisible par 7. En effet si p≥ 7, p! est
divisible par 7.
Donc an−a6=∑p=7np! est divisible par 7.
a1 = 1, a2 = 3, a3 = 32, a4 = 3 × 11, a5 = 32 × 17 et
a6 = 32 × 97 ne sont pas divisble par 7 lorsque n<7 et
an=a6+∑p=7np! a6 n’est pas divisible par 7
et ∑p=7np! est divisible par 7 donc an n’est pas divisible par 7
lorsque n≥ 7.
Donc an n’est jamais divisible par 7.
- an est divisible par 11 à partir d’un certain rang
On a an=a10+∑p=11np! .
a10=32 × 11 × 40787 est divisible par 11 et lorsque p≥ 11,
p! est divisible par 11 donc si n≥ 10, an est divisible par 11.
Donc an est divisible par 11 lorsque n≥ 10.
- an est divisible par 32 à partir d’un certain rang
8!=27*32*5*7 (avec Xcas, on tape ifactor(8!)) donc
pour p≥ 8 p! est divisible par 32.
On a an=a8+∑p=9np! .
a8=32 × 11 × 40787 est divisible par 32 et
lorsque p≥ 8,p! est divisible par 32.
Donc an est divisible par 32 lorsque n≥ 8. - an est n’est pas divisible par 33 à partir d’un certain rang
9!=27*34*5*7 (avec Xcas, on tape ifactor(8!)) donc
pour p≥ 9 p! est divisible par 34.
pour n≤ 8, an n’est pas divisible par 33 car :
a1 = 1, a2 = 3, a3 = 32, a4 = 3 × 11, a5 = 32 × 17
a6 = 32 × 97, a7 = 34 × 73, a8 = 32 × 11 × 467
On a an=a8+∑p=9np! pour n≥ 9.
a8 n’est pas divisible par 33 alors que ∑p=9np! est divisible
par 33 donc an n’est pas divisible par 33 lorsque n≥ 9.
Donc an n’est jamais divisible par 33.
6 Thème : Nombres complexes
6.1 L’exercice
Pour chaque question, une seule des 4 propositions est exacte. Cochez pour
chacune d’elle la bonne réponse sans justification.
-
Soit z ∈ C vérifiant z + |z| = 6 + 2i. L’écriture algébrique
de z est :
| ▫ | | −2i ▫ − | | −2i ▫ | | +2i ▫ − | | +2i |
- Dans le plan complexe, l’ensemble des points M d’affixe z = x + iy
vérifiant |z − 1| = |z + i| est la droite d’équation :
| ▫ y =x−1 ▫ y = −x ▫ y = −x + 1 ▫ y=x |
- Soit n un entier naturel. Le nombre (1+i√3)n est réel, si et
seulement si, n s’écrit sous la forme :
| ▫ 3k + 1 ▫ 3k + 2 ▫ 3k ▫ 6k |
- Soit l’équation (E) : z = 6−z/3−z (z∈ ℂ). Une solution
de (E) est :
| ▫ − 2 − | √ | | i ▫ 2 + | √ | | i ▫ | √ | | +i ▫ | √ | | + 2i |
- Dans le plan complexe, A et B étant les points d’affixes
respectives zA = −2 et zB =2i, l’ensemble des points M d’affixe z =x+iy
vérifiant la relation argz+2/z−2i=π/2 est inclus dans :
▫ La droite d’équation y = −x ▫ La droite d’équation y = x
▫ Le cercle{| de centre | I(1 + i) |
| de rayon | |
▫ Le cercle de diamètre [AB]
6.2 Le travail demandé au candidat
En aucun cas , le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
une justification des réponses aux questions 3) et 5) du QCM ;
un ou plusieurs exercices se rapportant au thème "Nombres complexes".
Le candidat présentera au jury :
le contenu de ses fiches ;
pour chaque item de ce QCM, les mréthodes et les savoirs mis en jeu
pour trouver la réponse exacte.
6.3 Solution de l’exercice avec Xcas
On configure le CAS en cochant Complex et Varianles_complexe
(menu Cfg->Configuration du CAS).
-
z + |z| = 6 + 2i
Avec Xcas, on tape :
solve(abs(z)^2=(6+2*i-conj(z))^2,z)
On obtient : [8/3-2*i] - |z − 1| = |z + i|
Avec Xcas, on tape :
csolve(abs(z-1)^2=abs(z+i)^2,z)
On obtient : [‘ x‘+(i)*(-‘ x‘)]
ou on tape :
csolve(abs(a-1+i*b)^2-abs(a+i+i*b)^2,a)
On obtient : [-b]
donc la droite a pour équation y=−x - (1+i√3)n est réel, si et seulement si, n s’écrit ...
Avec Xcas, on tape :
abs(1+i*sqrt(3)),arg(1+i*sqrt(3))
On obtient : 2, pi/3)
solve(n*pi/3=k*pi,n)
On obtient : [3*k] - z = 6−z/3−z
Avec Xcas, on tape :
solve(z =(6-z)/(3-z),z)
On obtient : [sqrt(2)*(i)+2,-sqrt(2)*(i)+2] - zA =−2, zB =2i, argz+2/z−2i=π/2
argz+2/z−2i est l’angle MB,MA
Donc on cherche M tel que :
MB,MA=π/2
Le lieu de M est le demi-cercle de diamètre AB contenant le point
d’affixe 0. Donc M se trouve sur le cercle de diamètre AB.Avec Xcas, on tape :
On définit les points A et B d’affixe -2 et 2i :
A:=point(-2);B:=point(2i);
On définit la fonction f par :
f(z):=(z+2)/(z-2i)
On cherche la fonction réciproque de f :
normal(csolve(f(z)=Z,z))
On obtient :
[((2*i)*Z+2)/(Z-1)]
On définit g la fonction réciproque de f par :
g(Z) :=((2*i)*Z+2)/(Z-1)
g n’est pas définit pour Z=1.
On définit les points C qui ont comme argument π/2 et pour cela on
définit un paramètre formel c>0 qui sera l’ordonnée de C :
supposons(c=[3.9,0,10,0.1])
C:=point(i*c)
On définit les points M qui sont les images des points C par g :
M:=point(g(i*c))
On demande d’avoir la trace des positions de M quand on fait varier c :
trace(M)
On obtient :

On vérifie que la trace correspond à :
arc(A,B,pi)
On tape pour avoir l’affixe de M :
normal(affixe(M))
On obtient :
((2*i)*c-2*i)/(c+i)
On tace alors le lieu de M :
plotparam(((2*i)*c-2*i)/(c+i),c=0..100)
et on obtient l’arc de cerccle AB passant par O.
7 Thème : Recherche de lieux géométriques
7.1 L’exercice
On dira qu’un triangle ABC non aplati possède la propriété P
si ses deux médianes issues de A et de B sont perpendiculaires.
-
Soit un triangle ABC ayant pour côtés AB=1, AC=√2 et
BC=√3.
Vérifier que le triangle ABC est rectangle et possède la propriété
P.
- Les deux points A et B étant fixés, on cherche à déterminer
l’ensemble Γ des points C tels que le triangle ABC possède la
propriété P. Trouver le lieu des points G, isobarycentre des trois
points A, B, C, lorsque C décrit Γ. En déduire l’ensemble
Γ.
- Soit ABC un triangle possédant la propriété P . On pose a=BC,
b=AC et c=AB.
Montrer que l’on a la relation a2+b2=5c2.
7.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse à la question 2) et un énoncé plus détaillé de
cette question à proposer à des élèves de première S;
un ou plusieurs exercices se rapportant au thème
"Recherche de lieux géométriques".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
7.3 Solution de l’exercice avec Xcas
-
Un triangle ABC a pour côtés AB=1, AC=√2 et
BC=√3.
On fait la figure avec Xcas. Dans un niveau de géométrie, on tape :
A:=point(0);
B:=point(1);
C:=inter(cercle(A,sqrt(2)),cercle(B,sqrt(3)));
triangle(A,B,C[0]);
triangle(A,B,C[1]);
A1:=milieu(B,C[1]);
B1:=milieu(A,C[1])
segment(A,A1);
segment(B,B1);
G:=inter_unique(segment(A,A1),segment(B,B1));
On obtient :

On a BC2=3 et AC2+AB2=2+1=3 donc BC2=AC2+AB2 et d’après Pythagore
le triangle ABC est rectangle en A.
Soient A1 (resp B1) le milieu de BC (resp AC). On a :
AA1=BC/2=√3/2 et
BB12=AB2+(AC/2)2=1+1/2=3/2 donc
BB1=√3/√2
Le centre de gravité G est donc tel que :
AG=√3/3 et BG=2/3*√3/√2=√6/3 donc
AG2+BG2=1/3+2/3=1=AB2
Donc d’après Pythagore le triangle GAB est rectangle en G. Le triangle
ABC a donc la propriété P.
- Si le triangle ABC a la propriété P c’est que le triangle GAB est
rectangle en G. Donc G se trouve sur le cercle de diamètre AB.
Soit C1 le milieu de AB.
On sait que :
Si dans un triangle ABC, avec C1 milieu de AB, on a un point G du
segment [CC1] qui vérifie C1C=3C1G alors G est le centre de
gravité du triangle ABC.
C se déduit de G par l’homothétie de centre C1 et de rapport 3.
On fait la figure avec Xcas.
Dans un niveau de géométrie, on tape :
A:=point(0);
B:=point(1);
c:=cercle(A,B):;c;
triangle(A,B,C);
assume(a=[1,-5,5,0.1])
G:=element(c,a);
C1:=milieu(A,B);
C:=homothetie(C1,3,G);
triangle(A,B,C);
trace(C);
segment(C1,C);
c3:=homothetie(C1,3,c):;
affichage(c3,1)
En faisant bouger le curseur a, on obtient la trace de C qui
coïncide avec le cercle en rouge qui est le cercle(point(1/2),3/2) :
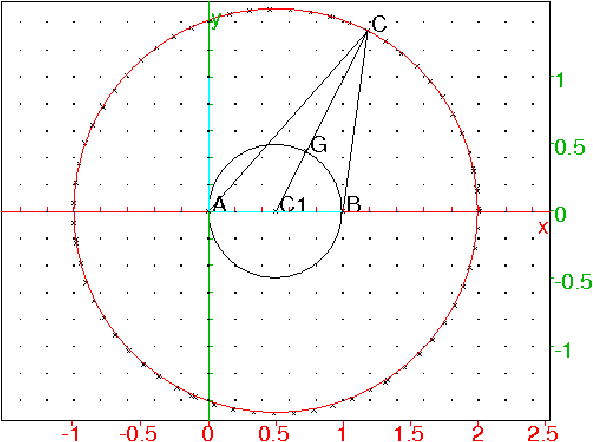
- Soit ABC ayant la propriété P. 0n a alors la relation a2+b2=5c2.
On complète la figure ci-dessus :
B1:=milieu(A,C);
A1:=milieu(B,C);
segment(A1,A);
segment(B1,B);

Les triangles : ABG, A1BG, AB1G sont rectangles en G donc :
c2=BG2+AG2, a2/4=A1G2+BG2 et b2/4= AG2+B1G2
On a G est le centre de gravité donc AG=2A1G et BG=2B1G donc
a2/4=A1G2+4B1G2, b2/4=B1G2+4A1G2 et
(a2+b2)/4=5(A1G2+B1G2)
c2=4B1G2+4A1G2 donc
a2+b2=5c2.
Remarque
A1 est le transformé de G par l’homothétie h1 de centre A
et de rapport 3/2.
C est le transformé de A1 par l’homothétie h2 de centre B
et de rapport 2.
Donc C est le transformé de G par l’homothétie h=h2∘ h1.
h a comme rapport 2× 3/2=3 et comme centre I
vérifiant :
J=h1(I)=h2−1(I) c’est à dire :
AJ=3/2AI,
BJ=1/2BI=1/2(BA+AI) et AJ−BJ=AB donc
3AI=3/2AB c’est à dire I est
le milieu C1 de AB.
Le même problème posé différemment
Soit un losange ABEF de centre G.
Soient A1 le milieu de GF, B1 le milieu de GE et C l’intersection de
(AA1) et (BB1).
Montrer que G est le centre de gravité du triangle ABC et que lorsqu’on
pose a=BC, b=AC et c=AB, on a a2+b2=5c2.
Il suffit de remarquer que les triangles GAB est l’image de GA1B1
dans l’homothétie de centre G et de rapport 2 (GA=2GA1 et GB=2GB1)
Donc AB=2A1B1 et AB//A1B1 et d’après le "théorème des milieux" on en
déduit que A1 est le milieu de BC et B1 est le milieu de AC.
Si d1 et d2 sont les longueurs des demi-diagonales du losange ABEF, on a:
d12+d22=c2, d12+d22/4=a2/4 et d12/4+d22=b2/4
donc a2+b2=5c2.
On a aussi :
A1 est le transformé de G dans l’homothétie de centre A et de
rapport 3/2.
C est le transformé de A1 dans l’homothétie de centre B et de
rapport 2.
On fait la figure avec Xcas.
Dans un niveau de géométrie, on tape :
A:=point(0);
B:=point(1);
assume(b=[1,-5,5,0.1]);
losange(A,B,b,E,F,affichage=2);
G:=milieu(A,E);
A1:=milieu(G,E);
B1:=milieu(G,F);
segment(A,E);
segment(B,F);
segment(A1,B1)
d1,d2:=droite(A,B1),droite(B,A1):;
d1;d2;
triangle(A,B,C,affichage=1);
C:=inter_unique(d1,d2);
trace(C);
On obtient :

8 Thème : Intégration
8.1 L’exercice
On considère la fonction numérique f de la variable réelle x
définie sur l’intervalle [0, +∞[ par :
-
On considère la fonction F définie sur [1, +∞[ par
F(x) = ∫1xf (t)dt
1.a) Démontrer que, pour tout réel t positif on a :
t+2≥ 2√2√t.1.b) En déduire que, pour tout x∈ [1, +∞[, on a :
1.c) À l’aide d’une intégration par parties, montrer que, pour tout
x∈ [1, +∞[, on a :
| ∫ | | (t + 2)e1−t dt= 4−(x + 3)e1−x |
1.d) En déduire que, pour tout x∈ [1, +∞[ on a :
0 ≤ F (x)≤ √2.
- On considère la suite (un) définie pour tout entier naturel n
non nul par :
Pour tout entier naturel n supérieur ou égal à 2, on note Sn la somme des
n−1 premiers termes de la suite (un). Exprimer Sn à l’aide d’une
intégrale. Montrer que la suite (Sn) converge et donner un encadrement de
sa limite.
8.2 Le travail demandé au candidat
En aucun cas , le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse à la question 2) ;
un ou plusieurs exercices se rapportant au thème "Intégration".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
8.3 Solution de l’exercice avec Xcas
-
On tape :
f(x):=sqrt(x)*exp(1-x)
F(x):=int(f(t),t,1,x)
1.a) Pour tout x≥ 0, on a f(x)= √x e1−x≥ 0 et
pour tout x≥ 1, on a √x≥ 1 donc
F(x)≥ ∫1xe1−tdt≥ 1.
Pour tout réel t positif on a :
t+2− 2√2√t=(√2 − √t)2≥ 0.
1.b) Pour tout x∈ [1, +∞[, on a d’après 1.a) :
√t ≤ 1/2√2(t+2) donc
1.c) Pour tout x∈ [1, +∞[, on intègre ∫1x(t + 2)e1−t dt
par parties et on pose :
u=t+2 et dv=e1−tdt donc du=dt et v=−e1−t on a donc
∫1x(t + 2)e1−t dt=[−(t+2)*e1−t]t=1t=x+∫1xe1−tdt donc
∫1x(t + 2)e1−t dt=[−(t+3)*e1−t]t=1t=x= 4−(x + 3)e1−x
Avec Xcas, on tape (le deuxième argument est u) :
A:=integrer_par_parties_u((t + 2)*exp(1-t),t + 2,t,1,x)
On obtient :
[-x*exp(-x+1)-2*exp(-x+1)+3,exp(-t+1)]
On tape (integrer_par_parties_u a comme synonyme ibpu et le deuxième argument est ici 0 pour terminer l’intégration) :
normal(ibpu(A,0,t,1,x))
On obtient :
-x*exp(-(x-1))-3*exp(-(x-1))+4
On peut aussi taper
int((t + 2)*exp(1-t),t,1,x) pour obtenir directement le résultat.
1.d) Pour tout x∈ [1, +∞[ on a (x + 2)e1−x≥ 0 et
(x + 3)e1−x≥ 0 donc
0 ≤ ∫1x(t + 2)e1−t dt=[−(t+3)*e1−t]t=1t=x= 4−(x + 3)e1−x≥ 4 donc
0 ≤ F (x)≤ √2.
- Pour tout x≥ 0, on a f(x)= √x e1−x≥ 0 donc pour tout
n> 0, on a un =∫nn+1f (t)dt≥ 0 et
pour tout n≥ 2, on a Sn=∑j=1n−1uj=∫1nf (t)dt=F(n) donc
Sn est croissante.
On sait d’après 1. que pour tout x∈ [1, +∞[, on a
1 ≤ F (x)≤ √2 donc Sn est croissante et majorée donc
convergente et on a pour tout n≥ 2 :
1≤ F(n) = Sn≤ √2
Remarques
On va essayer de trouver un meilleur minorant.
-
Pour trouver un minorant on peut calculer des valeurs approchées de
l’intégrale. On cherche les points d’inflexions du graphe de f :
le zéro de f″(x) est a=1+√2/2.
L’intégrale ∫x=1af(x)dx peut être minorée par la
méthode des trapèzes et les intégrales
∫x=a3/2f(x)dx et
un=∫x=nn+1f(x)dx peuvent être minorées par la
méthode du point milieu.
On tape :
a:=(1+sqrt(2))/2
areaplot(f(x),x=1..a,trapeze)
On obtient : 1.96
Ou on tape :
(f(1)+f(a))/2.*(a-1)
On obtient : 0.196042763728
On tape :
areaplot(f(x),x=a..3/2,point_milieu)
On obtient : 0.239
Ou on tape :
f((a+3/2)/2.)*(3/2-a)
On obtient : 0.239276873725
Il reste à minorer ∫3/2+∞f(x)dx par les aires des
rectangles au "point-milieu" : ils ont comme dimension 1× f(n) et donc
la somme de leurs aires est
∑n=2+∞f(n)=∑n=2+∞√n e/en=∑n=0+∞√n+2 1/en+1.
Commme √n+2 ≥ √2, on minore à nouveau cette somme par
√2/e∑n=0+∞ 1/en
c’est à dire par √2./ee/e−1)=√2./e−1.
On tape :
sqrt(2.)/(e-1)
On obtient : 0.82303935184
On a donc comme minnoration de la limite :
(f(1)+f(a))/2.*(a-1)+f((a+3/2)/2.)*(3/2-a)+ sqrt(2.)/(e-1)
On obtient : 1.25835898929
d’où un encadrement de la limite l :
| 1.25835898929 ≤ l ≤ 1.41421356237 |
- On peut avoir une meilleure valeur approchée de cette limite, si on
sait que ∫0+∞exp(−t2)dt=√π/2.
En effet en faisant le changement de variable x=t2, dx=2tdt donc
∫0+∞f(x)dx=e∫0+∞√(x)exp(−x)dx=2e∫0+∞t2exp(−t2)dt
On intégre par partie cette dernière intégrale (u=t, dv=2texp(−t2)dt) :
2e∫0+∞t2exp(t2)dt=e∫0+∞exp(−t2)dt
Soit on sait que ∫0+∞exp(−t2)dt=√π/2,
soit on fait le calcul en encadrant :
∫∫Cexp(x2+y2)dxdy
(C=[0,b]×[0,b]) avec
∫∫D1exp(x2+y2)dxdy (D1=x2+y2<b, x>0,y>0) et
∫∫D2exp(x2+y2)dxdy (D1=x2+y2<b√2, x>0,y>0).
On a donc :
Pour avoir une minoration de l’intégrale ∫01f(t)dt on utilise
-
la méthode des trapèzes :
On tape :
areaplot(f(x),x=0..1,20,trapeze)
On obtient :
1.02
- le développement de taylor à l’odre 5 de exp(−x) au voisinage de 0.
On tape :
g:=truncate(taylor(f(x)))
int(g,x=0..1.)
On obtient :
1.02963209244
donc comme on a une série alternée on a
1.02963209244≤ ∫x=01f(x)dx
Pour avoir une majoration de l’intégrale ∫01f(t)dt on utilise
-
la méthode du point milieu :
On tape :
areaplot(f(x),x=0..1/2,10,point_milieu)
On obtient :
0.481
On tape :
areaplot(f(x),x=1/2..1,10,point_milieu)
On obtient :
0.551
donc une majoration de ∫01f(t)dt est 0.481+0.551=1.032
- le développement de taylor à l’odre 6 de exp(−x) au voisinage de 0.
On tape :
h:=truncate(taylor(f(x),x=0,6),6)
int(h,x=0..1.)
On obtient :
1.03013547797
donc comme on a une série alternée on a
∫x=01f(x)dx≤ 1.03013547797
On a donc :
e√π/2−1.032<l<e√π/2−1.02
donc avec les calculs approchés de l’intégrale on a
| 1.37701454735<l<1.38901454735 |
et
| 1.37887906938<l<1.37938245491 |
avec le développement de Taylor à l’ordre 5 et 6.
Avec Xcas, on tape :
l:=int(f(x),x=1..inf)
On obtient :
-(sqrt(pi))/2*erf(1)*exp(1)+1+(sqrt(pi))/2*exp(1)
où erf(1) renvoie la valeur approchée de :
2/√π∫01(exp(−t2)dt)
On tape :
evalf(l)
On obtient :
1.37893607807
9 Thème : Fonctions, équations
9.1 L’exercice
On considère l’équation (E) : sin(x)−x/2=0, x∈ ℝ
-
Montrer que si x est solution de cette équation alors x appartient
à l’intervalle [-2, 2]
- Donner, en le justifiant, le nombre de solutions de l’équation (E).
- Donner une valeur approchée, à 10−3 près par défaut, de la
plus grande solution en précisant la méthode utilisée.
9.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse à la question 2) ;
un ou plusieurs exercices se rapportant au thème
"Fonctions, équations".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
9.3 Solution de l’exercice avec Xcas
-
On sait que −1≤ sin(x) ≤ 1 donc si on a x=2sin(x) alors
−2 ≤ x ≤ 2
On tape :
- Pour connaitre le nombre de solutions de
(E) : sin(x)−x/2=0, x∈ ℝ, on trace les deux graphes de
y=sin(x) et de y=x/2.
On tape :
plotfunc([sin(x),x/2])
On obtient :
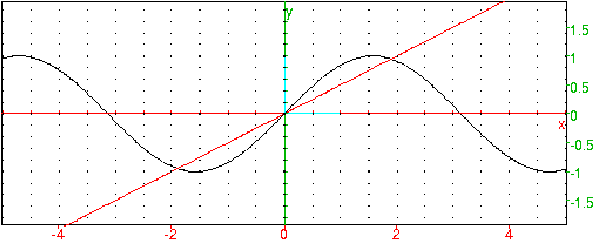
On voit alors que (E) a 3 solutions : pour le montrer cherchons le tableau
de variation de la fonction impaire g(x)=x/2−sin(x).
On tape :
g(x):=x/2-sin(x)
solve(diff(g(x)),x)
On obtient : [pi/3,(-pi)/3]
On tape :
solve(diff(g(x))>0,x)
On obtient :
[x<((-pi)/3),x>(pi/3)]
On tape :
g(0)
On obtient :
0
On tape :
limit(g(x),x,inf)
On obtient : +(infinity)
On tape :
normal(g(pi/3))
On obtient :
1/6*pi+(-(sqrt(3)))/2
On tape :
g(2.)
On obtient :
0.0907025731743
On tape :
g(1.8)
On obtient :
-0.0738476308782
On cherche les points d’inflexion, on tape :
solve(diff(diff(g(x))),x)
On obtient :
[0,pi]
On tape :
solve(diff(diff(g(x)))>0,x)
On obtient :
[((x>0) && (x<pi))]
La fonction g est donc convexe sur [pi/3,pi] et on a g(π/3)>0
On cherche avec Xcas les zéros de g(x) par la méthode de Newton on
tape :
fsolve(g(x),x,3,newton_solver)
On obtient :
1.89549426703
ou bien
On peut procéder par dichotomie :
On tape :
g(1.9)
On obtient : 0.00369991231258
On tape :
g(1.89)
On obtient : -0.00448561486462
On tape :
g(1.895),g(1.896)
On obtient : -0.000404700060102,0.00041432788413
donc x0≃ 1.895 par défaut à 10−3 près.
ou bien
On peut faire un programme de la méthode de Newton pour trouver la valeur par
défaut à 10−3 près.
L’intersection (b;0) de l’axe des x avec la tangente au graphe de g au
point (a;g(a) vérifie : 0=g′(a)(b−a)+g(a) i.e. b=a−g(a)/g′(a)
La suite qui converge vers x0 est donc :
un+1=un−g(un)/g′(un) avec u0=a et a ∈ [π/3,π] avec g(a)>0,
par exemple a=π ou a=3...
On calcule les différents termes de cette suite que l’on met dans la variable
a et on s’arrete quand g(a)*g(a−eps)≤ 0 avec ici eps=0.001.
solnew(g,a,eps):={
local h;
h:=function_diff(g)
tantque g(a)*g(a-eps)>0 faire
a:=a-g(a)/h(a);
ftantque;
retourne a-eps,a
}:;
On tape :
solnew(g,3.,0.001)
On obtient un encadrement de la limite à eps=0.001 prés :
1.89465262755,1.89565262755
10 Thème : Probabilités
10.1 L’exercice
Dans un lycée qui ne reçoit pas d’interne, la répartition des
élèves se fait de la façon suivante :
| Niveau | Seconde | Première | Terminale | Total |
| Externes | 50 | | 85 | 195 |
| Demi-pensionnaires | 285 | 220 | | |
| Total | | | 280 | |
Rappel de notation : PB(A) est la probabilité de A sachant que B
est réalisé.
-
Compléter le tableau ci-dessus.
- On rencontre un élève du lycée au hasard. On note E
l’événement "l’élève rencontré est externe", T "l’élève
rencontré est en terminale" et S l’événement "l’élève rencontré
est en seconde ". En supposant que tous les élèves ont la même
probabilité d’être rencontrés, calculer les probabilités suivantes :
2.a) P (E ∩ S).
2.b) P(E ∩ T) où E est l’événement
contraire de E.
- 3.a) Les événements E et T sont-ils indépendants ? Justifier votre
réponse.
3.b) Citer deux événements incompatibles.
- Calculer les probabilités conditionnelles suivantes : PS(E) et
PE (T ).
10.2 Le travail demandé au candidat
En aucun cas , le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse aux questions 2) et 3);
un ou plusieurs exercices se rapportant au thème "Probabilités"
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
10.3 Solution de l’exercice sans Xcas
-
On compléte le tableau :
| Niveau | Seconde | Première | Terminale | Total |
| Externes | 50 | 60 | 85 | 195 |
| Demi-pensionnaires | 285 | 220 | 195 | 700 |
| Total | 335 | 280 | 280 | 895 |
- 2.a) Calcul de P (E ∩ S).
Il y a un total de 895 élèves.
Il y 50 élèves qui sont externes et en Seconde".
Donc P (E ∩ S)=50/895=10/179
2.b) Calcul de P(E ∩ T)
Il y 195 élèves qui sont Demi-pensionnaires et en Terminale".
Donc P (E ∩ T)=195/895=39/179
- 3.a) Les événements E et T sont indépendants si on a :
P(E∩ T)=P(E)× P(T).
P(E∩ T)=85/895=17/179
P(E)=195/895=195/895=39/179
P(T)=280/895=195/895=56/179
donc E et T ne sont pas indépendants.
3.b) S "l’élève rencontré est en seconde "et T "l’élève
rencontré est en Terminale " sont incompatibles.
- Calcul de PS(E)
On sait que :
PS(E)× P(S)=P(E ∩ S)
On a :
P(S)=335/895=67/179
P(E ∩ S)=285/895=57/179
Donc PS(E)=57/67
On peut aussi dire il y a 335 élèves en seconde et parmi ces élèves
il y a 285 Demi-pensionnaires donc
PS(E)=285/335=57/67
Calcul de PE(T)
On sait que :
PE(T)× P(E)=P(E ∩ T)
On a :
P(E)=195/895=39/179
P(E ∩ T)=85/895=17/179
Donc PE(T)=17/39
On peut aussi dire il y a 195 élèves en externes et parmi ces élèves
il y a 85 en terminale donc
PE(T)=85/195=17/39
11 Thème : Arithmétique
11.1 L’exercice
-
Déterminer deux entiers relatifs u et v tel que 7u − 13v = 1
puis déterminer tous les couples (a, k) d’entiers relatifs tels que
14a − 26k = 4.
- On considère deux entiers naturels a et b. Pour tout entier n, on
note f(n) le reste de la division euclidienne de an+b par 26. On décide
de coder un message, en procédant comme suit : à chaque lettre de l’alphabet
on associe un entier compris entre 0 et 25, selon le tableau suivant :
| Lettre | A | B | C | D | E | F | G | H | I | J | K | L | M |
| Nombre | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Lettre | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| Nombre | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Pour chaque lettre du message, on détermine l’entier n associé puis on
calcule f(n).
La lettre est alors codée par la lettre associée à f(n). On sait que
la lettre F est codée par la lettre K et la lettre T est codée par la
lettre O.
2.a) Montrer que les entiers a et b sont tels que :
⎧
⎨
⎩ | | 5 | a + b | ≡ | 10 | (mod 26) |
| 19 | a + b | ≡ | 14 | (mod 26) |
|
|
2.b) En déduire qu’il existe un entier k tel que 14a − 26k = 4.
2.c) Déterminer tous les couples d’entiers (a,b), avec
0≤ a ≤ 25 et 0≤ b ≤ 25, tels que :
⎧
⎨
⎩ | | 5 | a + b | ≡ | 10 | (mod 26) |
| 19 | a + b | ≡ | 14 | (mod 26) |
|
|
2.d) On suppose que a = 17 et b = 3. Coder le message "GAUSS".
11.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse à la question 1) et à la question 2.c) ;
au moins deux méthodes différentes permettant de dḿontrer que pour
tous réels strictement positifs a et b on a :
(a+b/2)2≥ ab
un exercice se rapportant au thème "Arithmétique ".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
11.3 Solution de l’exercice avec Xcas
-
On cherche deux entiers relatifs u et v tel que 7u − 13v = 1
Avec Xcas, on tape :
iabcuv(7,-13,1)
On obtient : [2,1]
En effet 2*7-1*13=1
Ou bien on tape :
iegcd(7,-13)
On obtient : [2,1,1]
On cherche tous les couples (a,k) d’entiers relatifs tels que 14a−26k=4.
Avec Xcas, on tape :
iabcuv(14,-26,4)
On obtient une solution : [4,2]
En effet 4*14-2*26=4
Pour avoir toutes les solution on remarque que :
14(a−4)−26(k−2)=0 ou encore 7(a−4)=13(k−2)
Puisque 7 et 13 sont premiers entre eux, on en déduit que :
pour tout n∈ ℤ on a a−4=n*13 et que k−2=n*7
Les solutions sont donc a=4+13n, k=2+7n pour tout n∈ ℤ
Remarque : si on tape :
iegcd(14,-26)
On obtient : [2,1,2]
car le pgcd de 14 et 26 est 2. - 2.a) Avec Xcas, on tape pour définir f:
f(n,a,b):=irem(a*n+b,26)
On obtient :
Pour définir le codage on utilise la commande ord (ord("A")=65)
et pour le décodagela commande char (char(65)="A").
On tape :
code(S):=ord(S)-65
decode(L):=char(L+65)
On tape :
codage(S,a,b):={
local n,m;
n:=code(S);
m:=irem(a*n+b,26);
return decode(m);
}:;
On sait que codage("F")="K" et codage("T")="O".
On a :
code("F")=5 et code("K")=10 et
code("T")=19 et code("O")=14 donc on doit avoir :
irem(5*a+b,26)=10 et irem(19*a+b,26)=14
Donc il existe deux entiers relatifs m et p tels que :
5a+b=26*m+10 et 19a+b=26*p+14
ou encore
⎧
⎨
⎩ | | 5 | a + b | ≡ | 10 | (mod 26) |
| 19 | a + b | ≡ | 14 | (mod 26) |
|
|
2.b) En déduire qu’il existe un entier k tel que 14a − 26k = 4.
D’après 2.c) il existe deux entiers relatifs m et p tels que :
5a+b=26*m+10 et 19a+b=26*p+14 .
Donc par soustraction (si k=p−m) : (19−5)a=14a=26*k+4
ou encore 14a−26k=4
2.c) On cherche donc tous les couples d’entiers (a,b), tels que :
0≤ a ≤ 25, 0≤ b ≤ 25, 14a−26k=4, 5a+b=26*m+10
D’après 1) on a 14a−26k=4, a=4+13n, k=2+7n pour tout n∈ ℤ
On veut 0≤ a ≤ 25 donc n=1, a=17 et k=9.
5a+b=85+b=26*m+10 donc b=26*m−75≡ 3 (mod 26).
Donc a=17 et b=3
Avec Xcas, on tape :
codage("F",17,3),codage("T",17,3)
On obtient : ("K","O")
2.d) On code le message "GAUSS".
Avec Xcas, on tape :
codages(S,a,b):={
local j,n,m,l,R;
l:=size(S);
R:="";
pour j de 0 jusque l-1 faire
n:=code(S[j]);
m:=irem(a*n+b,26);
R:=R+decode(m);
fpour;
return R;
}:;
On tape :
codages("GAUSS",17,3)
On obtient : "BDFXX"
On vérifie et on tape :
codage("G",17,3),codage("A",17,3),codage("U",17,3), codage("S",17,3)
On obtient : "B","D","F","X"
Remarque Au lieu de la commande ord, on peut utiliser la commande
asc qui renvoie une liste (asc("A")=[65]).
12 Thème : Utilisation des variations d’une fonction
12.1 L’exercice
-
Pour tout réel x>0, on pose : f(x)=x−1−ln(x).
Étudier les variations de la fonction f et en déduire que pour tout
réel x > 0, on a :
- Soient a, b et c des réels strictement positifs : on pose
m=a+b+c/3. En appliquant l’inégalité précédente
aux réels, a/m, b/m et
c/m, montrer que :
12.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse à la question 2) ;
au moins deux méthodes différentes permettant de dḿontrer que pour
tous réels strictement positifs a et b on a :
un exercice se rapportant au thème "Utilisation des variations d’une
fonction".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
12.3 Solution de l’exercice avec Xcas
-
On tape :
assume(x>0)
f(x):=x-1-ln(x)
solve(diff(f(x))>0,x)
On obtient :
[x>1]
f est donc décroissante sur ]0;1] et croissante sur [1;+∞[. Le
minimum de f(x) sur ]0;+∞[ est donc f(1).
On tape : f(1)
On obtient :
0
donc f(x) ≥ 0 c’est à dire ln(x)≥ x − 1
- On a si m=a+b+c/3:
ln(a/m)=ln(a)−ln(m)≤ a/m − 1 (idem pour b/m et c/m) donc
ln(a)+ln(b)+ln(c)−3ln(m)≤ (a+b+c)/m − 3 ou encore
ln(abc/m3)≤ (a+b+c)/m − 3=0
On a donc montrer que abc/m3≤ 1 ou encore
abc≤ m3=(a+b+c/3)3
- Montrer que (a+b/2)2≥ ab :
On tape :
factor((a+b)^2-4a*b)
On obtient :
(a-b)^2
donc (a+b/2)2≥ ab
On peut voir cette inégalité graphiquement :
 dans le dessin on voit que l’on peut mettre 4 rectangles de côtés
a× b dans le carré ABCD d’aire (a+b)2 et qu’il
reste un carré d’aire (a−b)2 et donc on a (a+b)2≥ 4ab.
dans le dessin on voit que l’on peut mettre 4 rectangles de côtés
a× b dans le carré ABCD d’aire (a+b)2 et qu’il
reste un carré d’aire (a−b)2 et donc on a (a+b)2≥ 4ab.Autre démonstration proche de l’exercice :
On pose m=a+b/2 et on a
ln(a/m)=ln(a)−ln(m)≤ a/m − 1 donc
ln(ab/m2)=ln(a)+ln(b)−2ln(m)≤ (a+b)/m − 2=0 donc
ab≤ m2=(a+b/2)2
13 Thème : Géométrie dans l’espace
13.1 L’exercice
Dans cet exercice, les questions sont indépendantes. Pour chaque question,
une seule des trois propositions a), b) ou c) est exacte. On demande d’indiquer
laquelle, sans justification.
L’espace est rapporté à un repère orthonormal
(O;i, j, k).
-
Soient A et B deux points distincts de l’espace. L’ensemble des
points M de l’espace tels que
||M A|| = ||M B|| est :
a) l’ensemble vide b) un plan c) une sphère - On considère les points E(0;1;−2) et F(2;1;0). Les coordonnées du
barycentre G du système de points pondérés {(E;1), (F; 3)} sont :
a) G(6; 4; −2) b) G(1.5;1;−0.5) c) G(0.5;1;1.5) - Soit d la droite de représentation paramétrique :
x=2−t; y = 3t; z = −3, t∈ R.
On considère les points A(2;3;−3), B(2;0;−3) et C(0;6;0). On a :
a) d =(AB) b) d = (BC) c) d≠ (AB) et
d ≠ (BC) et d ≠ (CA) - La droite de représentation paramétrique :
x=−4t; y=1+3t; z=2+2t, t∈ R, et le plan d’équation :
x − 2y + 5z − 1 = 0 sont :
a) orthogonaux b) parallèles c) ni orthogonaux ni
parallèles. - L’ensemble des points tels que x−y+2z−1=0 et −2x+4y−4z+1=0 est :
a) l’ensemble vide b) une droite c) un plan
13.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse aux questions 3) et 4) du QCM;
un ou plusieurs exercices se rapportant au thème "Géométrie dans l’espace".
Le candidat présentera au jury :
le contenu de ses fiches ;
pour chaque item de ce QCM, les méthodes et les savoirs mis en jeu pour
trouver la réponse exacte.
13.3 Solution de l’exercice avec Xcas
-
L’ensemble des points M de l’espace tels que
||M A|| = ||M B|| est le plan médiateur
du segment AB (réponse b)).
On peut faire la figure avec Xcas, on ouvre un niveau 3D (Alt+h),
on se met en mode (Mode->point),
on clique sur 2 points A et B et on tape :
segment(A,B)
mediatrice(A,B)
On obtient :
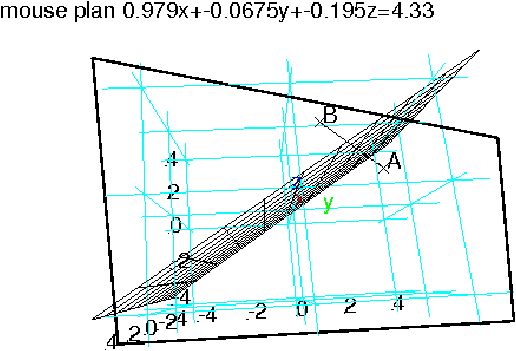
- SoientE(0;1;−2) et F(2;1;0). Le barycentre G du système de points pondérés {(E;1), (F; 3)} vérifie :
OG=1/4(OE+3OF).
Donc G a pour coordonnées (3/2;1;−1/2) (réponse b)).
On peut faire la figure avec Xcas, on ouvre un niveau 3D (Alt+h)
et on tape :
E:=point([0,1,-2])
F:=point([2,1,0])
G:=barycentre([E,1],[F,3])
coordonnees(G)
On obtient :
[3/2,1,-1/2]
- Soient d la droite x=2−t; y = 3t; z = −3, t∈ R et les points
A(2;3;−3), B(2;0;−3) et C(0;6;0).
Si A ∈ d alors t=0 ce qui n’est pas vrai car yA≠ 0 (mais B ∈ d pour t=0), donc d ≠ AB et d ≠ CA
C ∉ d car zC=0≠−3 donc d ≠ AB et d ≠ CB
(réponse c)).
On peut faire la figure avec Xcas, on ouvre un niveau 3D (Alt+h),
et on tape :
d:=plotparam([2-t,3t,-3],t,affichage=1+epaisseur_ligne_3));
legende(point(1,3,-3),"d",rouge)
A:=point([2,3,-3])
B:=point([2,0,-3])
C:=point([0,6,0])
droite(A,B,affichage=4+epaisseur_ligne_3)
droite(A,C,affichage=2+epaisseur_ligne_3)
droite(C,B,affichage=3+epaisseur_ligne_3)
plan(z=-3)
demi_droite([0,0,0],[1,0,0])
demi_droite([0,0,0],[0,1,0])
demi_droite([0,0,0],[0,0,1])
legende(point(1,0,0),"i",rouge)
Ox_3d_unit_vector(affichage=1+epaisseur_ligne_3)
legende(point(0,1,0),"j",vert)
Oy_3d_unit_vector(affichage=2+epaisseur_ligne_3)
legende(point(0,0,1),"k",bleu)
Oz_3d_unit_vector(affichage=4+epaisseur_ligne_3)
On obtient :

- Soient la droite d
x=−4t; y=1+3t; z=2+2t, t∈ R, et le plan P x − 2y + 5z − 1 = 0.
d est parallèle au vecteur v=[−4,3,2] et le vecteur n=[1,−2,5] est
normal à P.
On a v.n=−4*1+3*(−2)+2*5=0
donc v est orthogonal à n.
Donc d et P sont parallèles (réponse b)).
On peut faire la figure avec Xcas, on ouvre un niveau 3D (Alt+h),
et on tape :
d:=droite([0,1,2],[-4,4,4])
P:=plan(x-2y+5z-1=0)
est_parallele(d,P)
On obtient : 1
- Les points tels que x−y+2z−1=0 et −2x+4y−4z+1=0 sont sur
l’intersection des plans P d’équation x−y+2z−1=0 et Q d’équation
−2x+4y−4z+1=0.
Ces deux plans ne sont ni confondus ni parallèles puisque
les vecteurs normaux à ces plans : nP=[1,−1,2] et nQ=[−2,4,−4] ne sont
pas colinéaires (cross([1,-1,2],[-2,4,-4])=[-4,0,2]!=[0,0,0])donc
ces points sont sur une droite (réponse b)).
On peut faire la figure avec Xcas, on ouvre un niveau 3D (Alt+h),
et on tape :
P:=plan(x-y+2z-1=0):;affichage(P,1);
Q:=plan(-2x+4y-4z+1=0):;affichage(Q,4);
d:=inter(P,Q,affichage=2+epaisseur_ligne_4);
demi_droite([0,0,0],[1,0,0]);
demi_droite([0,0,0],[0,1,0]);
demi_droite([0,0,0],[0,0,1]);
On obtient :
14 Thème : Divers types de raisonnement
14.1 L’exercice
Les propositions suivantes sont indépendantes. Pour chacune d’elles,
préciser si elle est vraie ou fausse en justifiant votre réponse.
-
Toute suite numérique non majorée tend vers +∞.
- La somme d’une suite convergente et d’une suite divergente est une suite
divergente.
- Il existe un nombre réel a et un nombre réel b, tels que
e2a + e2b < 2 √e2a × e2b.
- Il existe une fonction f continue en un point x0 et non dérivable
en x0.
14.2 Le travail demandé au candidat
En aucun cas , le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse aux questions 2) et 3);
un ou plusieurs exercices se rapportant au thème "Divers types de
raisonnement" dans des domaines variés (arithmétique, géométrie,
dénombrement, analyse, ...).
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
14.3 Solution de l’exercice sans Xcas
-
C’est faux, par exemple (−1)n*n ou n*sin(n) ou
(u2n=n,u2n+1=1)
- Si la suite u est convergente et la suite v est divergente alors
la suite w=u+v est divergente est une proposition vraie.
On fait une démonstration par l’absurde :
Si la suite w est convergente et la suite u est convergente alors
la suite v=w−u est convergente car on sait (ou on montre) que la somme
algébrique de 2 suites convergentes est convergente.
- On fait une démonstration par l’absurde :
Si il existe a et b tels que :
e2a+e2b<2√e2a× e2b, alors
on pose A=ea et B=eb.
Puisque A>0 et B>0 on a
√A2)× B2=A× B et l’inégalité s’écrit :
A2+B2−2A× B=(A−B)2<0 ce qui est
faux.
Donc il n’existe pas a et b vérifiant une telle inégalité.
Ou bien on fait une démonstration directe :
Puisque √e2a× e2b=ea× eb, on a
e2a+e2b<2√e2a× e2b est èquivalent à :
e2a+e2b−2√e2a× e2b=(ea−eb)2<0
et ceci est faux quelque soit a et b. - Il existe une fonction f continue en un point x0 et non dérivable
en x0. C’est vrai par exemple f(x)=|x| est continue en x0=0, mais
n’est pas dérivable en x0=0.
15 Thème : Étude de configurations
15.1 L’exercice
Dans le plan rapporté à un repère orthonormal
(O;i,j), on considère la courbe (C)
d’équation y =1/x avec x∈ ]0, +∞[. Soit a un réel
strictement positif.
-
La droite (Da), tangente à (C) au point A d’abscisse a, coupe
l’axe des abscisses en Pa et l’axe des ordonnées en Qa. Déterminer
les coordonnées de Pa et Qa et montrer
que l’aire du triangle OPa Qa est indépendante du réel a.
- On considère un réel k >2/a. On note (Δk) la droite
parallèle à (Da) et passant par le point de coordonnées (0, k).
Montrer que lorsque k varie dans l’intervalle ]2/a, ∞+[,
la droite (Δk ) coupe la courbe (C) en deux points Bk et Ck et
que le milieu Ik de [Bk , Ck ] est aligné avec O et A.
15.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse à la question 2)
un exercice se rapportant au thème "Étude de configurations".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
15.3 Solution de l’exercice avec Xcas
-
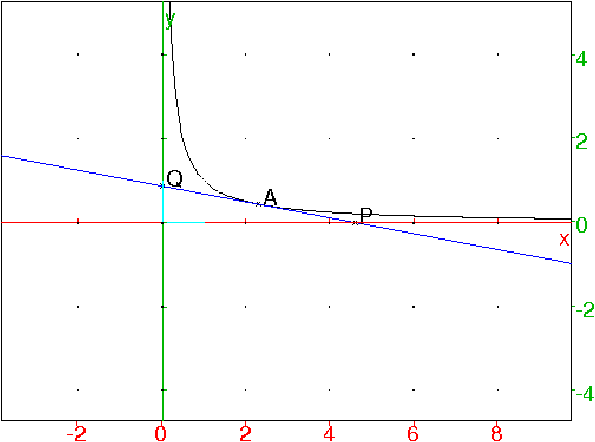
On tape :
supposons(a=[2.3,0,10,0.1]);
C:=plotfunc(1/x,x=0 .. 10);
A:=point(a,1/a);
D:=tangente(C,A):;affichage(D,4);
P:=inter_unique(D,droite(y=0));
Q:=inter_unique(D,droite(x=0));
On obtient :
On tape :
normal(equation(D))
On obtient :
y=((2*a-x)/(a^2))
On tape :
coordonnees(P)
On obtient :
[2*a,0]
On tape :
coordonnees(Q)
On obtient :
[0,1/a*2]
On tape :
area(triangle(0,P,Q)
On obtient :
2
- On tape pour continuer la figure :
supposons(a=[1.4,0,10,0.1]);
C:=plotfunc(1/x,x=0 .. 10);
A:=point(a,1/a);
D:=tangente(C,A):;affichage(D,4);
P:=inter_unique(D,droite(y=0));
Q:=inter_unique(D,droite(x=0));
supposons(k=[3.7,2/a,10,0.1]);
K:=point(0,k,affichage=quadrant3);
Δ:=parallele(K,D,affichage=1);
[B,C]:=inter(C,Δ);
I:=milieu(B,C);
droite(A,I);
On obtient :

On tape :
est_aligne(0,A,I)
On obtient :
1
16 Thème : Propriétés des fonctions
16.1 L’exercice
Les questions sont indépendantes. Dans chacun des cas suivants, proposer unefonction f qui vérifie les propriétés données. On donnera
l’expression de f(x).
-
f est une fonction définie sur ℝ par :
La limite de f en +∞ est +∞ et l’équation f(x)=0 admet deux
solutions, 0 et ln(2).
- f est une fonction définie sur ]0, +∞[, f(2)=4 et, pour tout
x et tout y strictement positifs on a :
- f est une fonction polynôme de degré supérieur ou égal à 2
et la valeur moyenne de f sur [-2, 2] est 0.
- f est une fonction paire, non constante, définie sur ℝ telle que
pour tout x∈ ℝ on a :
16.2 Le travail demandé au candidat
En aucun cas , le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse aux questions 2) et 4);
un ou plusieurs exercices se rapportant au thème "Propriétés des
fonctions".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
16.3 Solution de l’exercice avec Xcas
-
f est une fonction définie sur ℝ par :
f (x) = ae2x + bex + c
La limite de f en +∞ est +∞ donc a>0 et l’équation f(x)=0
admet deux solutions, 0 et ln(2) donc si on pose X=ex, l’équation
aX2+bX+c=0 admet deux solutions, e0=1 et eln(2)=2 donc :
aX2+bX+c=a(X−1)(X−2)=a(X2−3X+2).
La fonction f (x) =e2x −3ex + 2 répond à la question.
Avec Xcas, on vérifie :
On tape :
f(x):=exp(2x) -3*exp(x)+ 2
limit(f(x),x=inf)
On obtient :
+(infinity)
On tape :
solve(f(x))
On obtient :
[0,ln(2)]
- f est définie sur ]0, +∞[, f(2)=4 et, pour tout
x et tout y strictement positifs on a :
f(xy) = f(x) + f(y)
On sait que si k=cste, g(x)=k*ln(x) vérifie g(x+y)=g(x)+g(y).
La relation f(2)=4 va nous permettre de déterminer k
g(2)=4=k*ln(2) donc k=4/ln(2).
On choisit de prendre f(x)=4*ln(x)/ln(2)
Avec Xcas, on vérifie :
On tape :
f(x):=4*ln(x)/ln(2)
f(2)
On obtient :
4
On tape :
lnexpand(f(x*y))
On obtient :
(4*(ln(y)+ln(x)))/(ln(2))
- f est un polynôme de degré supérieur ou égal à 2
et la valeur moyenne de f sur [-2, 2] est 0.
Donc f(x) est une fonction impaire, le polynôme sera constitué de
monômes de degré impair. On choisit par exemple : f(x)=x3
Avec Xcas, on vérifie :
On tape :
f(x):=x^3
int(f(x),x=-2..2)
On obtient :
0
- f est une fonction paire, non constante, définie sur ℝ telle que
pour tout x∈ ℝ on a :f(x+1)=f(x).
f est périodique de période 1 et f est paire. La fonction
f(x)=cos(2*x) répond à la question car elle est paire, non constante,
définie sur ℝ telle que
pour tout x∈ ℝ on a :f(x+1)=f(x).
Avec Xcas, on vérifie :
On tape :
f(x):=cos(2*pi*x)
f(-x)
On obtient :
cos(2*pi*x)
On tape :
normal(trigexpand(expand(f(x+1))-f(x)))
On obtient :
0
17 Thème : Probabilités
17.1 L’exercice
On place dans une urne 100 billets de loterie dont seulement 2 sont gagnants.
-
Un joueur achète deux billets, qu’il tire simultanément dans l’urne.
1.a) Quelle est la probabilité de ne pas gagner ?
1.b) En déduire la probabilité d’avoir au moins un billet gagnant. - Soit n un entier (n≥ 2). Un joueur achète n billets, qu’il
tire simultanément dans l’urne.
Soit An l’événement : "Avoir 1 ou 2 billet(s) gagnant(s) en ayant n
billets".
2.a) Décrire avec une phrase l’événement An,
événement
contraire de An.
2.b) Montrer que la probabilité de l’événement An est :
2.c) Quel est le nombre minimum n0 de billets à acheter pour que la
probabilité d’avoir au moins 1 billet gagnant soit supérieure ou égale
à 1/2 ?
17.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse à la question 2.b) ;
un ou plusieurs exercices se rapportant au thème
"Probabilités".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
17.3 Solution de l’exercice sans Xcas
-
1.a) la probabilité de ne pas gagner
On ne gagne pas si on a choisit les 2 billets parmi les 98 billets non
gagnants. On a donc comb(98,2) possibilités. Le nombre total de choix
est comb(100,2). la probabilité de ne pas gagner est donc :
comb(98,2)/comb(100,2).
On tape :
comb(98,2)/comb(100,2)
On obtient : 4753/4950
1.b) "Avoir au moins un billet gagnant" est l’événement contraire à
"Avoir aucun un billet gagnant", la probabilité de gagner est donc :
1-comb(98,2)/comb(100,2).
Avec Xcas, on tape :
1-comb(98,2)/comb(100,2)
On obtient : 197/4950
C’est aussi 2/100*98/99+98/100*2/99+2/100*1/99
- 2.a) L’événement An est :
"Avoir aucun billet gagnant en ayant n billets".
2.b) On ne gagne pas si on a choisit les n billets parmi les 98 billets non
gagnants. On a donc comb(98,n)=98!/n!(98−n)! possibilités.
Le nombre total de choix est comb(100,n)=100!/n!(100−n)!. la probabilité de ne pas gagner est donc
98!n!(100−n)!/n!(98−n)!100!=(100−n)(99−n)/100 × 99.
Donc:
2.c) Si la probabilité d’avoir au moins 1 billet gagnant est supérieure ou
égale à 1/2, c’est que la probabilité d’avoir 0 billet gagnant
est inférieure strictement à 1/2.
On cherche n tel que :
(100−n)(99−n)/100*99<1/2 ou encore
2(100−n)(99−n)−9900<0.
On tape :
solve((100-n)*(99-n)/9900-1/2<0,n) ou
solve(2*(100-n)*(99-n)-9900<0,n)
On obtient :
[((n>(1/2*(199-sqrt(19801)))) && (n<(1/2*(199+sqrt(19801)))))]
On tape :
evalf(1/2*(199-sqrt(19801)))
On obtient :
29.1419869524
Donc n0=30.
On vérifie et on tape :
(100-29)*(99-29)/9900.,(100-30)*(99-30)/9900.
On obtient :
0.50202020202,0.487878787879
18 Thème : Équations différentielles
18.1 L’exercice
On se propose d’étudier les fonctions f dérivables sur [0, +∞[
vérifiant la condition :
| (1)
| ⎧
⎨
⎩ | | pour tout x ∈ [0, +∞[, f (x)f′(x) = 1 |
| f(0)=1 |
|
|
-
On se propose de démontrer qu’une fonction vérifiant la condition (1)
est strictement positive sur [0, +∞[.
1.a) Montrer que si la fonction f vérifie (1) alors f ne s’annule pas sur
[0, +∞[.
1.b) On suppose que la fonction f vérifie la condition (1) et qu’il existe
un réel a strictement positif tel que f (a) < 0. En déduire que
l’équation f (x) = 0 admet au moins une solution dans l’intervalle
[0, a].
1.c) Conclure. - Existence et unicité de la fonction :
2.a) Soit u une fonction dérivable sur un intervalle I. Déterminer une
primitive de la fonction uu′ sur cet intervalle.
2.b) En déduire que si f est telle que, pour tout x ∈ [0, +∞[,
f(x)f′(x) = 1 alors il existe une constante C telle que pour tout
x ∈ [0, +∞[,
2.c) On rappelle que f (0) = 1. Déterminer l’expression de f (x) pour
x réel positif.
18.2 Le travail demandé au candidat
En aucun cas, le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse aux questions 1.b) et 2.b) ;
un ou plusieurs exercices se rapportant au thème
"Équations différentielles".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
18.3 Solution de l’exercice sans Xcas
-
1.a) On sait que pour tout x ∈ [0, +∞[, f (x)f′(x) = 1 donc
pour tout x ∈ [0, +∞[, f (x) ≠ 0
1.b) Si il existe a>0 telle que f(a)<0 alors puisque f(0)=1>0 et que f
est dérivable, d’après
le théorème des valeurs itermédiaires il existe b∈ ]0;a[ tel que
f(b)=0
1.c) Comme f ne s’annule pas, on en déduit qu’il n’est pas possible
qu’un tel a existe donc pour tout x ∈ [0, +∞[, f (x)>0.
- 2.a) Une primitive de la fonction uu′ sur un intervalle I est
1/2u2
2.b) On sait que sur un intervalle les primitives d’une fonction sont égales
à une constante près. Une primitive de 1 sur [0, +∞[ est x et une
primitive de f(x)f′(x) est 1/2f(x)2 donc il existe une constante
C tel que :
pour tout x ∈ [0, +∞[, on a 1/2f(x)2=x+C
2.c) Puisque f(0)=1 on en déduit que C=1/2 c’est
à dire que pour tout x ∈ [0, +∞[, on a f(x)2=2x+1.
Puisque d’après 1) on sait que f(x)>0 sur [0, +∞[ on en déduit
que pour tout x ∈ [0, +∞[, on a f(x)=√2x+1
Remarque
Pourquoi se limite-t-on à [0, +∞[ ?
On a montré ici, que sur un intervalle I, on a :
f(x)>0 et f(x)2=2(x+C) avec C=cste donc
f est définie sur ]−C;+∞[.
Si f(0)=1, alors C=1/2 donc
f(x)=√2x+1 sur ]1/2; +∞[
18.4 Solution de l’exercice avec Xcas
Avec Xcas, on tape :
desolve((y*y’=1) and (y(0)=1),y)
On obtient :
[sqrt(2*x+1)]
On ouvre un niveau de géométrie 2-d et on tape :
plotfunc(sqrt(2x+1),x=-0.5..7,affichage=1+epaisseur_ligne_3
On peut alors avoir le champ des tangentes avec le menu :
Graphe->Slopefield Ode (2-d) on tape 1/y comme valeur de
dy/dt, puis on clique sur les points
donnant les différentes conditions initiales et on termine en changeant de
mode.
On obtient :

19 Thème : Arithmétique
19.1 L’exercice : L’âge du capitaine
Le capitaine a fait naufrage. Tout ce que l’on a retrouvé sur lui est sa
carte de sécurité sociale. On parvient à déchiffrer son numéro INSEE,
sauf le deuxième chiffre a et le troisième chiffre b qui sont
illisibles : 1ab1271153044 clé 67
Les deux chiffres a et b qui manquent sont, dans cet ordre, les deux
derniers chiffres de l’année de naissance du capitaine. On se propose
d’utiliser la clé du numéro INSEE pour retrouver cette année de naissance.
-
La clé K d’un numéro INSEE est calculée de la manière suivante :
K=97−R où R est le reste de la division euclidienne par 97 de l’entier N
constitué par les 13 premiers chiffres du numéro INSEE.
1.a) Démontrer que la clé K d’un numéro INSEE est telle que
N+K≡ 0 (mod 97).
1.b) Déduire que, pour le numéro INSEE du capitaine, on a :
N≡ 30 (mod 97).
- On écrit 1ab1271153044 = 1ab× 1010+A , où A=1271153044.
2.a) Calculer le reste de la division euclidienne de A par 97.
2.b) Justifier la congruence suivante : 102≡ 3 (mod 97).
2.c) En déduire que l’on a : 1010≡ 49 (mod 97).
- 3.a) Déduire des résultats établis aux questions 1) et 2) que l’on
a :
3.b) Vérifier que l’on a : 49 × 2≡ 1 (mod 97).
3.c) Déterminer l’année de naissance du capitaine.
19.2 Le travail demandé au candidat
En aucun cas , le candidat ne doit rédiger sur sa fiche sa solution de
l’exercice.
Celle-ci pourra néanmoins lui être demandée partiellement ou en
totalité lors de l’entretien avec le jury.
Le candidat rédigera sur ses fiches :
sa réponse à la questions 3);
un ou plusieurs exercices se rapportant au thème Arithmétique"".
Le candidat présentera au jury :
le contenu de ses fiches ;
les méthodes et les savoirs mis en jeu dans l’exercice.
19.3 Solution de l’exercice avec Xcas
Tout d’abord une remarque : on peut avoir 2 solutions pour les valeurs de a
et de b étant donné que l’on travaille dans ℤ/97ℤ.
Par exemple 1991271153044 % 97=1021271153044 % 97=8 % 97.
On suppose donc que 10a+b<97 ou 10a+b>3....
-
On a :
INSEE =1ab1271153044 clé 67 donc
N=1ab1271153044 et K=67
K=97−R=67 et
N=97*Q+R (avec Q∈ ℕ,R∈ ℕ et R<97)
1.a) On a N+K=97*Q+R+97−R=97*(Q+1) donc
N+K ≡ 0 (mod 97)
1.b) Puisque :
K=67, K ≡ −30 (mod 97) et
N+K ≡ 0 (mod 97)
on a N ≡ 30 (mod 97) - 1ab1271153044 = 1ab× 1010+A , où A=1271153044
2.a) Avec Xcas, on tape :
irem(1271153044,97)
On obtient :
54
Ou on tape :
1271153044 % 97
On obtient :
-43 % 97
donc A ≡ 54 (mod 97)
2.b) 102 ≡ 3 (mod 97) car 102=100=97+3
2.c) 1010 ≡ 49 (mod 97) car
1010=1005 ≡ 35=243 ≡ 49 (mod 97) (puisque 243=97*2+49)
- 3.a) Montrons que : 1ab × 49 ≡ 73 (mod 97).
On a :
N ≡ 30 (mod 97)
N=1ab1271153044 = 1ab × 1010+1271153044 =1ab × 1010+A
1010 ≡ 49 (mod 97) et
A≡ 54 (mod 97)
donc
N≡ 1ab× 49+54=30 (mod 97)
Donc 1ab× 49 ≡ 30−54=−24 (mod 97)
−24 ≡ 73 (mod 97) donc
1ab× 49 ≡ 73 (mod 97)
3.b) On a : 49 × 2≡ 1 (mod 97).
En effet 49*2=98=97+1.
Avec Xcas,
on tape :
inv(49 % 97)
On obtient :
2 % 97
3.c) Puisque :
1ab× 49 ≡ 73 (mod 97)
On a : 1ab× 49 × 2 ≡ 73× 2=146 (mod 97)
49 × 2 ≡ 1 (mod 97).
Donc 1ab ≡ 146 (mod 97)
Les deux derniers chiffres de l’année de naissance du capitain sont donc 46.
Avec Xcas, on pose 10*a+b=C et on a
N−30=1ab1271153014=(100+C)*1010+1271153014 ≡ 0 (mod 97)
On tape :
solve((100+C)*10^10+1271153014 %97,C)
On obtient :
[46]
Remarque
J’aurai préférai que le texte dise par exemple, que l’année de naissance
du capitaine est dans l’intervalle [1900 ;1997[. On cherche
les deux chiffres a et b qui manquent c’est à dire on cherche
un nombre entier C<97 sachant que (cf question 1.a) ;
N−30=1ab1271153014=(100+C)1010+1271153014 ≡ 0 (mod 97)
Puis, je trouve préférable de travailler avec le nombre C et non avec
l’écriture en base 10 du nombre 100+C=100+10a+b.
On continue ensuite de la même façon, on a :
100 %97=3 % 97,
1010 %97=243=49 %97,
1012 %97=3*49=50 %97
on a
(100+C)*1010+1271153014 ≡ 49*C+1271153064 ≡ 0 (mod 97)
1271153064 %97=−23 % 97 donc
49*C % 97=23 % 97
on cherche l’inverse de 49 dans ℤ/97ℤ, on a
49*2 %97=98 %97=1 %97 donc l’inverse de 49 dans ℤ/97ℤ est 2 %97.
Donc en multipliant membre à membre 49*C % 97=23 % 97 par 2 %97, on
a :
C % 97=46 % 97
Puisque 0≤ C<97 on en déduit que C=46 et donc que a=4 et b=6
Ce document a été traduit de LATEX par HEVEA













 dans le dessin on voit que l’on peut mettre 4 rectangles de côtés
a× b dans le carré ABCD d’aire (a+b)2 et qu’il
reste un carré d’aire (a−b)2 et donc on a (a+b)2≥ 4ab.
dans le dessin on voit que l’on peut mettre 4 rectangles de côtés
a× b dans le carré ABCD d’aire (a+b)2 et qu’il
reste un carré d’aire (a−b)2 et donc on a (a+b)2≥ 4ab.




