Un peu de géométrie des polygones.

Un polygone est une figure plane délimitée par des segments de droite, qu’on appelle les côtés, un point se situant à l’extrémité de deux arêtes est un sommet. Voici quelques exemples :

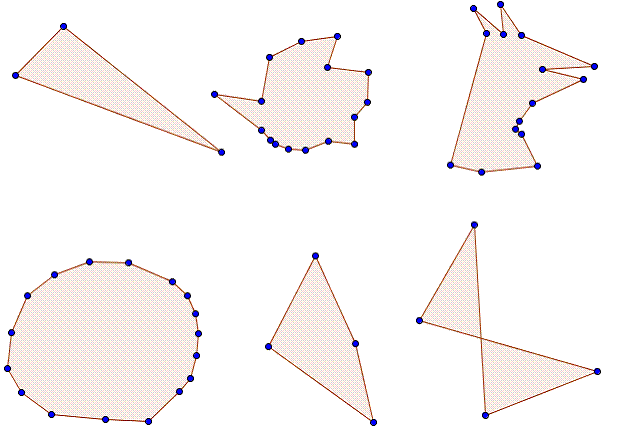
Nous observons des différences entre ces polygones, d’abord le nombre des sommets, ensuite le nombre de côtés, puis dans la forme. Soyons plus précis.

Le nombre de côtés est très important, ainsi nous parlerons de :

· Polygone à trois cotés ou triangle,

· Polygone à quatre côtés ou quadrilatère,

· Polygone à cinq côtés ou pentagone,

· Polygone à six côtés ou hexagone,

· Polygone à sept côtés ou heptagone,

· Polygone à huit côtés ou octogone,

· Polygone à neuf côtés ou ennéagone,

· Polygone à dix côtés ou décagone,

· Polygone à onze côtés ou hendécagone,

· Polygone à douze côtés ou dodécagone,

· Polygone à vingt côtés ou icosagone.

Pour la forme de la figure nous devons distinguer :

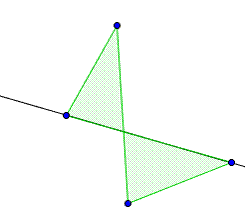
· Les polygones croisés dans lesquels deux côtés se rencontrent en un autre point que une extrémité.

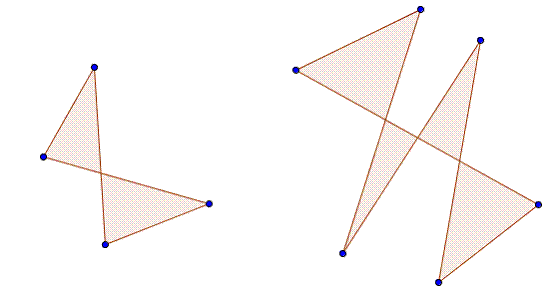
· Les polygones convexes : Chaque côté du polygone se prolonge en une droite, cette droite partage le plan en deux régions, si le polygone n’est pas partagé en deux régions alors on dit que le polygone est convexe sinon on dit que le polygone est étoilé.

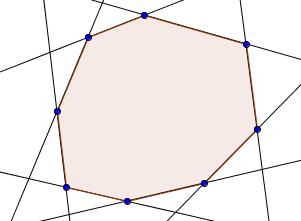
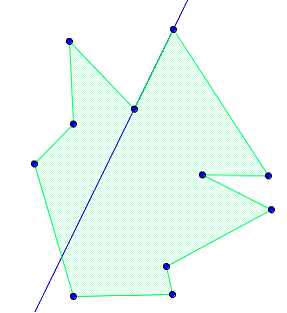
Le polygone de gauche est convexe et celui de droite est étoilé.

· Les polygones réguliers. Dans le langage courant un polygone régulier est un polygone convexe dont tous les angles ont la même mesure et tous les côtés la même longueur, mais nous pouvons parler aussi de polygones réguliers étoilés.

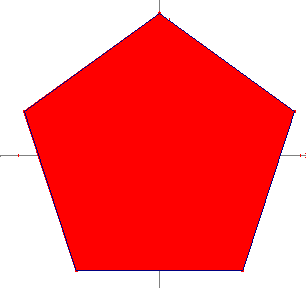
Les polygones réguliers convexes

Triangle équilatère	Carré

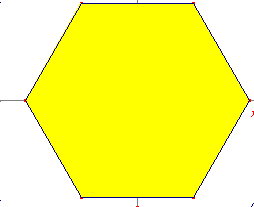
Pentagone régulier	Hexagone régulier

Les polygones réguliers étoilés

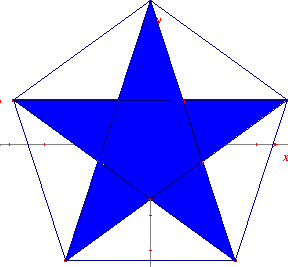
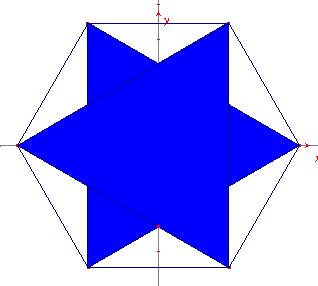
Pentagramme ou pentagone régulier étoilé	Hexagone régulier étoilé
Heptagone régulier étoilé {7/2}.	Heptagone régulier étoilé {7/3}.

Le premier est un pentagone étoilé, appelé aussi pentagramme et noté {5/2}.

Le second est un hexagone étoilé noté {6/2}.

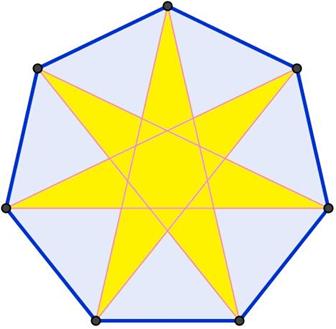
Le troisième est un heptagone mais nous avons plusieurs types de heptagones étoilés:

prenons pour point de départ un sommet et allons vers deux sommets plus loin,

recommençons de nouveau cette opération,

remarquez que après avoir épuisé tous les sommets et retrouvé notre point de départ

nous avons tourné deux fois autour du centre du heptagone, ce qui explique la notation {7/2}.

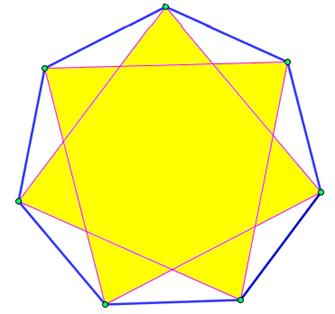
La figure suivante est aussi un heptagone étoilé et est noté {7/3}.

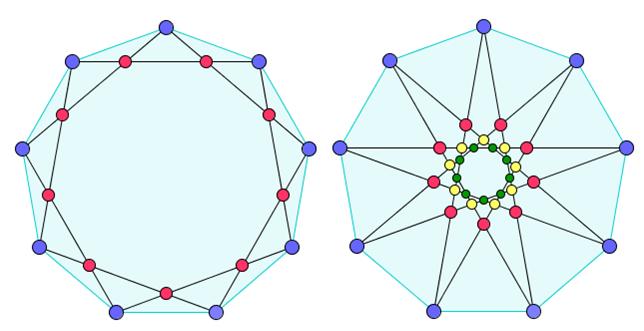
Les deux dernières figures sont les deux possibilités d’ennéagones étoilés {9/2} et {9/4}. Grace à cette figure nous pouvons donner une autre explication pour la terminologie {9/4}: remarquez qu’il y a quatre types de points dans l’ennéagone, à des niveaux différents, où les côtés se rencontrent, chaque type représenté par une couleur.

Les Polyèdres

Définitions :

§ Un polyèdre (du grec poly : plusieurs ; èdre : face) est un solide limité par un ensemble fini des polygones, appelés faces, tels que chaque côté d’un polygone de cet ensemble soit commun à un côté d’un autre polygone de cet ensemble.

§ Une arête du polyèdre est un côté commun à deux faces.

§ Un sommet du polyèdre est un point commun à au moins trois arêtes

§ Un polyèdre régulier est formé d’un ensemble fini des polygones réguliers convexes identiques.

§ Un polyèdre est convexe s’il peut être posé par n’importe quelle face sur une surface plane, comme par exemple une table.

La formule d’Euler : F + S = A + 2

Leonhard Euler (1750) a découvert la formule reliant le nombre de faces (F), le nombre de sommets (S) et le nombre d’arêtes (A) d’un polyèdre. Cette formule s’applique à tout polyèdre convexe.