I had to teach how to find the solution of an equation using the dichotomy method. A couple of weeks later I was listening to Constantin Vernicos who was explaining a construction using generalised ellipses that showing that synthetic Ricci curvature has somewhat limited applications: it doesn’t make much sense for certain metric spaces that arise naturally as limits of Riemannian spaces.
All the figures were made with matplotlib on an iPad Air.
An ellipse is the set of points x in the plane such that the sum of the distances to two fixed points, the foci, is D>0, i.e.
d(x,F1) + d(x,F2) = D
If the distance d(,) is associated to a norm ||.|| then this becomes:
f(v) := || v - F1 || + || v - F2 || - D = 0
Now we choose a circle C such that for all B \in C, f(B) > 0 and obviously f(A) <0. The sign change guarantees there is a solution i.e. a point of the ellipse on the segment AB.
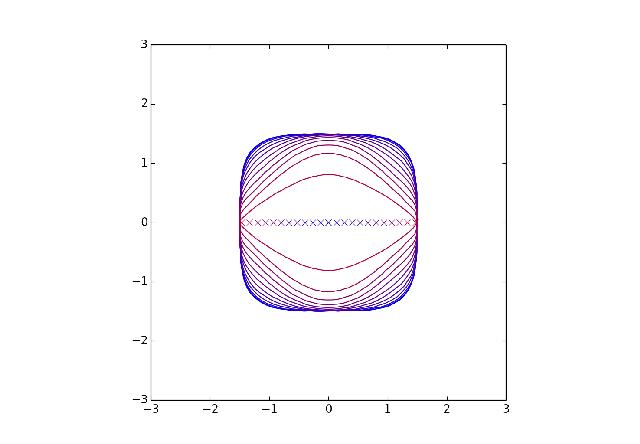
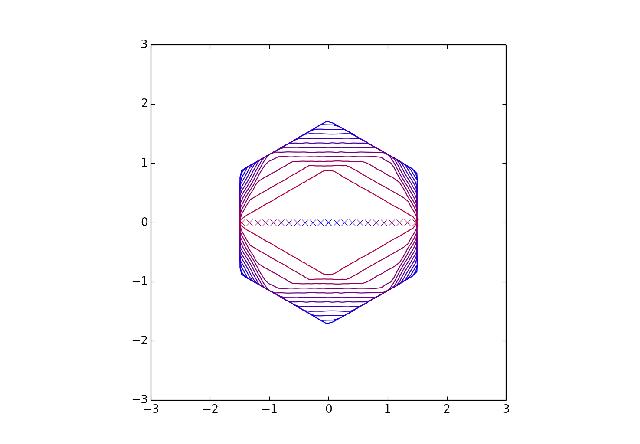
Then norms like the l_p norms and more generally || v || = max | v.u| with u\in (1,0), (0,1), (1,1)


Of course the method isn’t that great because C is a polygon with about 100 vertices but it is good enough to see what is going on.
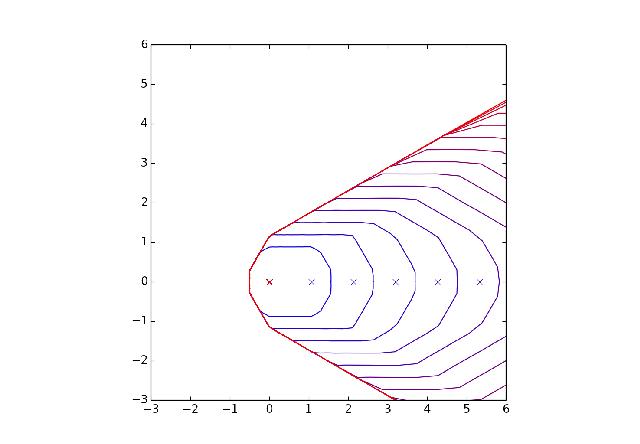
Here are some more. In each of the figures the outer ellipse is the boundary of a distance ball so that F1=F2. Subsequent ellipses are obtained by pulling F1 and F2 apart and the sequence of foci is marked by Xs. The final ellipse is not in general a line. Can you see why?


Here is a sequence of ellipses converging to a “parabola”.