Exemples de dynamique linéaire sur graphe

Table of Contents

1 Exemple 1: transport simple
2 Exemple 2: mélange
3 Exemple de Jordan
4 Exemple 3: matrice de Toeplitz
5 Exemple 5: modèle de generations

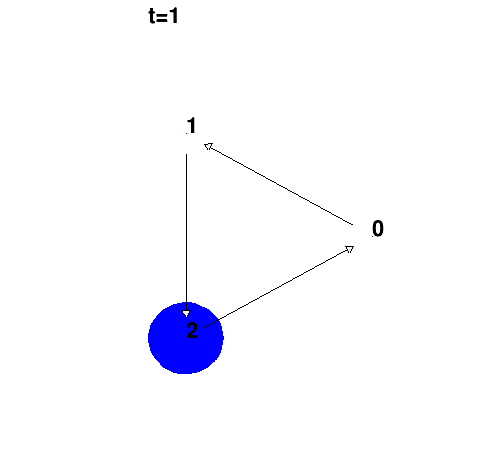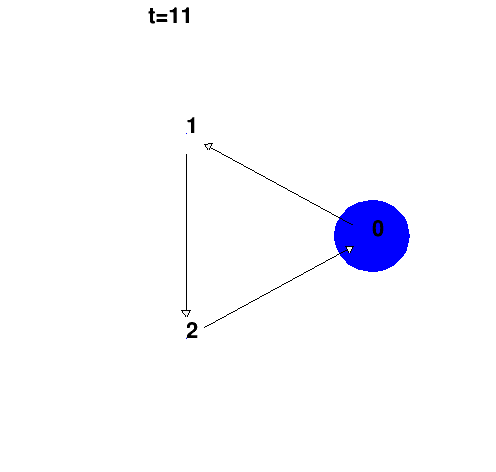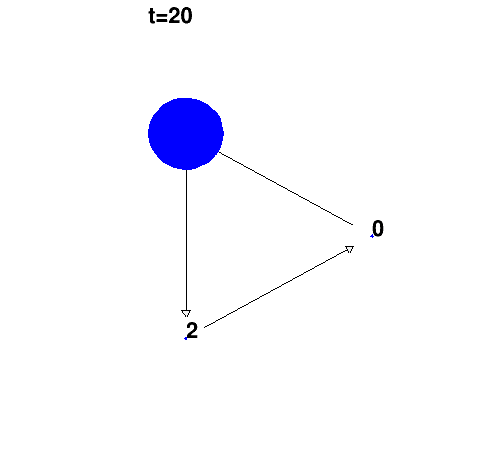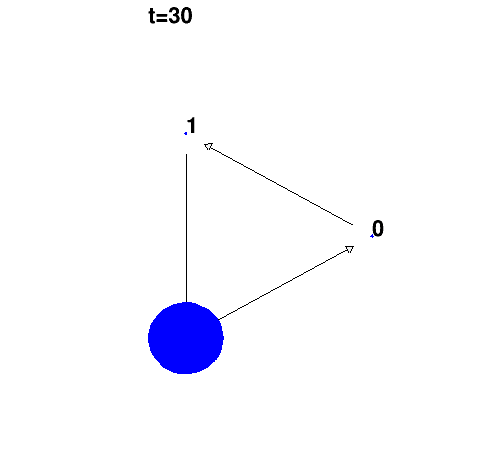
1 Exemple 1: transport simple

Matrice: M=( 0 0 1 1 0 0 0 1 0 )
C'est une matrice stochastique ( ∑ j M j,i =1 qui préserve les mesures de probabilité) et ergodique.
image: 0_home_faure_c++_syst_dynamiques_markov_rapport_animation_1.gif
Remarque: système à trois états.
Spectre et pseudo-spectre Vert ( z-M ) -1 Vert
image: 1_home_faure_c++_syst_dynamiques_markov_rapport_val_p_1.png      image: 2_home_faure_c++_syst_dynamiques_markov_rapport_pseudo_spectre_1.png

2 Exemple 2: mélange

Matrice: M=( 0.5 0 1 0.5 0 0 0 1 0 )
C'est une matrice stochastique et mélangeante.
image: 3_home_faure_c++_syst_dynamiques_markov_rapport_animation_2.gif
Remarque: converge vers l'état d'équilibre: U 0 =( 1/2 1/4 1/4 )
Spectre et pseudo-spectre Vert ( z-M ) -1 Vert
image: 4_home_faure_c++_syst_dynamiques_markov_rapport_val_p_2.png      image: 5_home_faure_c++_syst_dynamiques_markov_rapport_pseudo_spectre_2.png

3 Exemple de Jordan

Bien que spécial, on verra que cet exemple est essentiel.
Matrice de Jordan perturbée:, N=30 .
M=( 0 1.1 ⋱ ⋱ 1.1 ε 0 ), ε =0  ou  ε =0.1
image: 21_home_faure_c++_syst_dynamiques_markov_rapport_animation_J_a.gif image: 22_home_faure_c++_syst_dynamiques_markov_rapport_animation_J_b.gif
Norme Vert M t V(0) Vert 2 :
image: 20_home_faure_c++_syst_dynamiques_markov_rapport_Norme2_J_a.png image: 23_home_faure_c++_syst_dynamiques_markov_rapport_Norme2_J_b.png
Remarques: modélise une population de poissons sur une rivière avec barrages?
Converge vers un système à deux états (après renormalisation).
Spectre et pseudo-spectre Vert ( z-M ) -1 Vert
image: 24_home_faure_c++_syst_dynamiques_markov_rapport_val_p_J_a.png image: 25_home_faure_c++_syst_dynamiques_markov_rapport_val_p_J_b.png
image: 26_home_faure_c++_syst_dynamiques_markov_rapport_pseudo_spectre_J_a.png image: 27_home_faure_c++_syst_dynamiques_markov_rapport_pseudo_spectre_J_b.png

4 Exemple 3: matrice de Toeplitz

Matrice (de Toeplitz): M=( 0 1 0 1/4 ⋱ ⋱ ⋱ 0 1 ε 1/4 0 ), avec  ε =0 ou  ε =0.02
Ce n'est pas une matrice stochastique. C'est une matrice ergodique. La troisieme figure est normalisée.
image: 7_home_faure_c++_syst_dynamiques_markov_rapport_animation_3.gif image: 10_home_faure_c++_syst_dynamiques_markov_rapport_animation_4.gif image: 11_home_faure_c++_syst_dynamiques_markov_rapport_animation_4_b.gif
Norme Vert M t V(0) Vert 2 :
image: 8_home_faure_c++_syst_dynamiques_markov_rapport_Norme2_3.png image: 12_home_faure_c++_syst_dynamiques_markov_rapport_Norme2_4.png
Remarques: modélise une population de poissons sur une rivière avec barrages?
Converge vers un système à deux états (après renormalisation).
Spectre et pseudo-spectre Vert ( z-M ) -1 Vert
image: 9_home_faure_c++_syst_dynamiques_markov_rapport_val_p_3.png image: 13_home_faure_c++_syst_dynamiques_markov_rapport_val_p_4.png
image: 6_home_faure_c++_syst_dynamiques_markov_rapport_pseudo_spectre_3.png image: 14_home_faure_c++_syst_dynamiques_markov_rapport_pseudo_spectre_4.png

5 Exemple 5: modèle de generations

(ref: Trefethen p.461),
Matrice: M=( 0.15 ⋯ 0.15 0.9 ⋱ 0.9 ), puis M=( 0.18 ⋯ 0.18 0.9 ⋱ 0.9 ),
Ce n'est pas une matrice stochastique. C'est une matrice ergodique.
Dynamique, figure normalisée:
image: 15_home_faure_c++_syst_dynamiques_markov_rapport_animation_5.gif image: 28_home_faure_c++_syst_dynamiques_markov_rapport_animation_6.gif
Remarque: modélise la dynamique avec différentes tranches d'ages?
Norme Vert M t V(0) Vert 2 :
image: 16_home_faure_c++_syst_dynamiques_markov_rapport_Norme2_5.png image: 29_home_faure_c++_syst_dynamiques_markov_rapport_Norme2_6.png
Spectre et pseudo-spectre Vert ( z-M ) -1 Vert
image: 17_home_faure_c++_syst_dynamiques_markov_rapport_val_p_5.png image: 30_home_faure_c++_syst_dynamiques_markov_rapport_val_p_6.png
image: 18_home_faure_c++_syst_dynamiques_markov_rapport_pseudo_spectre_5.png image: 31_home_faure_c++_syst_dynamiques_markov_rapport_pseudo_spectre_6.png