Novembre 2020.
Attention: Pour lire ce document, utiliser Firefox qui donne un bon rendu des équations utilisant MathML.
1 Travail demandé
- Avant la séance de TP faire les exercices préparatoires donnés ci-dessous. Scanner et envoyez moi par email s'il vous plait, vos feuilles dans un seul fichier au format pdf sous la forme NOM_PRENOM.pdf. Remarque: sous android ou iphone, l'application CamScanner, permet de générer un fichier pdf à partir des photographies d'un document papier. Si vous n'y arrivez pas, informez moi.
- En séance de TP, faire les exercices de programmation sur ordinateur.
- Après la séance de TP, choisir un projet parmi cette liste et développer/réaliser le projet en s'aidant des exemples vus dans ce TP.
Langage informatique:
- Dans ce TP, on propose d'utiliser le langage python3 avec l'envirronement Spyder3. Voici un didacticiel Python avec de nombreuses références.
- Si vous préférez C++, voici le (presque) même tutorial pour C++, et voici un didacticiel C++ avec de nombreuses références.
Objectif
- La question centrale est de comprendre et prévoir le comportement à temps longs de systèmes gouvernés par des lois.
- Dans ce TP, à l'aide de quelques exemples précis, on explore la dynamique déterministe à temps continu (flot) ou temps discret en dimension , avec . Autrement dit à chaque instant , l'état du système est caractérisé par les variables .
- Pour une loi à temps continu, et la loi est de la formespécifiée par une fonction appelée champ de vecteur.
- Pour une loi à temps discret la loi est de la formeavec une fonction .
- Dans tous les cas, l'objectif est de comprendre, décrire le comportement des trajectoires pour .
- Rappels: technique utile: la section de Poincaré.
2 Dimension 1
2.1 Dynamique à temps continu en dimension 1
On considère
qui dépend de
et qui satisfait l'équation de mouvement
avec le paramètre
fixé. On appelle (
2.1) le
modèle de Verhulst, voir aussi
fonction de Verhulst. La fonction
s'interprète comme un champ de vecteur sur
.
2.1.1 Exercices mathématiques préparatoires
- Selon le paramètre , trouver les points fixes de la dynamique (2.1), c'est à dire les zéros du champ de vecteur , et déterminer leur stabilité, c'est à dire le signe de . Quels sont les attracteurs et répulseurs (i.e. attracteur dans le passé) de la dynamique?
- Calculer et déterminer si le flot est contractif, expansif ou conservatif selon .
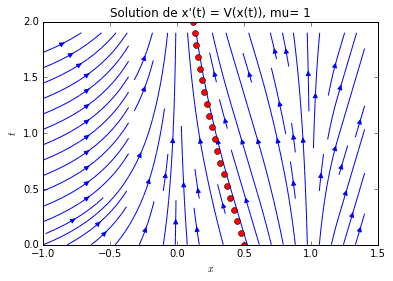
- Pour , (et ensuite ), tracer le graphe de la fonction et déduire l'allure du champ de vecteur sur l'axe . Remarquer que (2.1) est équivalent à considérer l'équation de mouvement du « problème étendu » , suivant:où il apparaît le champ de vecteur dans le plan . Tracer l'allure des trajectoires (ou « lignes d'univers ») dans le plan .
Solutions:
- est un zéro si donnant ou qui sont les deux points fixes du flot. On a . Si , alors montrant que pour , le point fixe est stable ( ou « attracteur ») et montrant que le point fixe est instable (ou « répulseur »).
- On a donc, si , alors on a pour , i.e. le flot est contractif (dissipatif). On a pour , i.e. le flot est expansif (dissipatif).
2.1.2 Exercice de programmation
- Télécharger et exécuter le programme champ_vecteur_dim1.py qui dessine le champ de vecteur dans le plan et résout l'équation (2.1) avec le schéma de Runge-Kutta. Aide: sous linux, dans un terminal écrire:
python3 champ_vecteur_dim1.py
- Lire et bien comprendre le programme.
- Changer la condition initiale et le paramètre dans le programme et vérifier vos prédictions.
- Modifier le programme pour étudier l'équation de mouvement suivante sur l'intervalle :
2.2
Dynamique à temps discret en dimension 1
On considère la variable
qui dépend du temps discret
et qui satisfait l'équation de récurrence
avec le paramètre
. On appelle (
2.3)
l'application logistique.
2.2.1 Exercices préparatoires
- Tracer le graphe de dans l'intervalle . Trouver le(s) point(s) fixe(s) et discuter leur stabilité en fonction de . Pour , quels sont les attracteurs et répulseurs de la dynamique?
- Calculer et déduire si l'application est contractive, expansive ou conservative selon .
- Optionnel. On pose et . On suppose , . Trouver les points fixes de (i.e. les points périodiques de de période deux) et discuter leur stabilité en fonction de . Tracer le graphe appelé diagramme de bifurcation.
- Montrer que est toujours attracteur.
2.2.2 Exercice de programmation
- Télécharger, compiler et exécuter le programme application_dim1.py qui dessine la fonction et fait évoluer le point .
- Changer la condition initiale et le paramètre dans le programme et vérifier vos prédictions.
- Changer la formule de l'application et essayer.
- Optionnel. Faire un programme qui dessine les attracteurs et répulseurs de la dynamique en fonction de , comme ici.
- Optionnel. Comme ici, considérer l'équation avec et . Faire un programme qui pour chaque paramètre , associe (ou une couleur) obtenu par: partant du point et , on pose . Cela fera apparaître l'ensemble de Mandelbrot.
3 Dimension 2
3.1 Dynamique à temps continu en dimension 2
On considère
qui dépend de
et qui satisfait l'équation de mouvement
avec le paramètre
. On appelle (
3.1) le
l'Oscillateur de Van der Pol. La fonction
s'interprète comme un
champ de vecteur sur
.
3.1.1 Exercices préparatoires
- Selon le paramètre , trouver les points fixes de la dynamique (2.1), c'est à dire les zéros du champ de vecteur , et déterminer leur stabilité.
- Calculer et déterminer si le flot est contractif, expansif ou conservatif selon le point .
3.1.2 Exercice de programmation
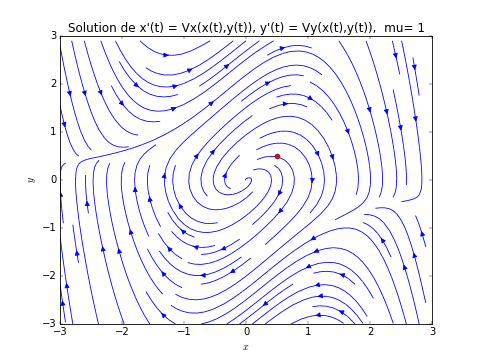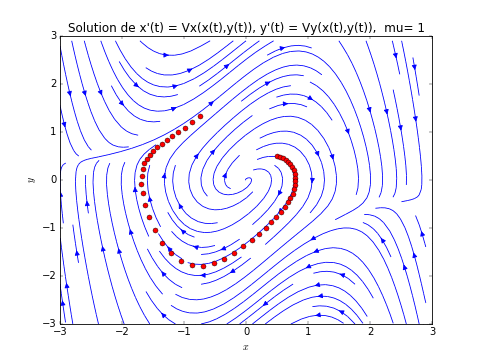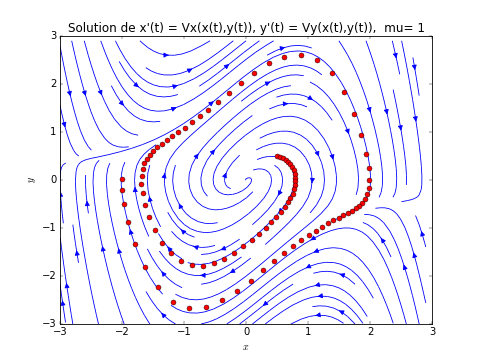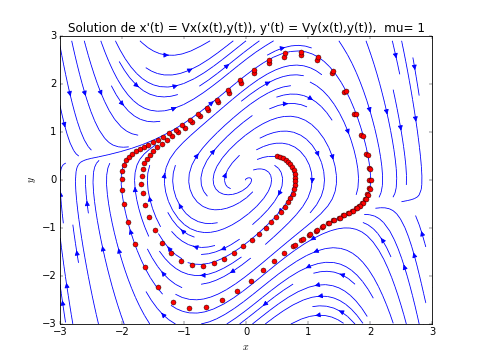
- Renommer le programme champ_vecteur_dim1.py ci-dessus en champ_vecteur_dim2.py. Le modifier afin de dessiner le champ de vecteur et la trajectoire comme l'image ci-dessus. Solution ici: 4.1.5.
- Changer la condition initiale et le paramètre dans le programme et vérifier vos prédictions.
3.1.3 (Optionnel) Section de Poincaré
- Considérer la demi droite dans le plan et considérer la suite des intersections d'une trajectoire avec . Cela définit une dynamique de dimension 1 à temps discret, appelée Section de Poincaré du flot. En utilisant la coordonnée sur , on a une suite . Exercice: avec le programme, afficher la suite . Tracer la fonction qui définit l'application de Poincaré et tracer les points comme dans la Section 2.2.
3.1.4 (Optionnel) Autres exemples
- Considérer un pendule amorti caractérisé par sa position angulaire .
Exercice 3.1.
Écrire les équations de mouvement comme un champ de vecteur dans l'espace de phase .
3.2 Dynamique à temps discret en dimension 2
On considère
qui dépend du temps discret
et qui satisfait l'équation de récurrence
,
avec le paramètre
. On appelle (
3.2)
l'application standard.
3.2.1 Exercices préparatoires
- On note . Calculer et déduire si l'application est contractive, expansive ou conservative selon le point .
- Allure des trajectoires si ?
3.2.2 Exercice de programmation
- Télécharger et exécuter le programme application_dim2.py qui dessine la trajectoire d'un point : Cliquer « bouton gauche » pour choisir un point initial, « barre espace » pour continuer la trajectoire.
- Observer les trajectoires.
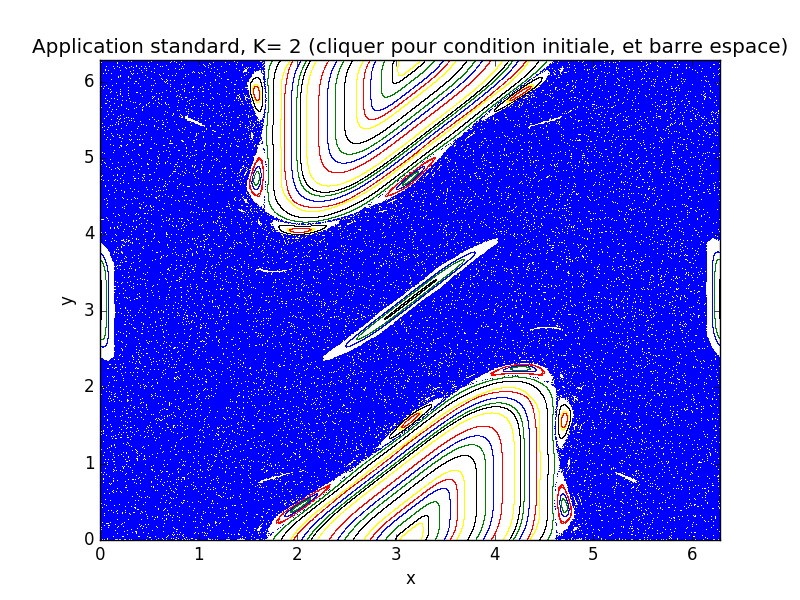
- Modifier le paramètre K pour reproduire la figure ci-dessous.
3.2.3 Autres exemples
- Considérer un domaine du plan , par exemple un disque de rayon . Une particule est libre de se déplacer dans ce domaine, i.e. avance en ligne droite à vitesse constante, et rebondit de façon parfaite sur le bord. A chaque rebond on note la position angulaire et où est l'angle par rapport à la direction normale. La suite des rebond définit une suite avec . qui est une dynamique à deux dimensions et temps discret.
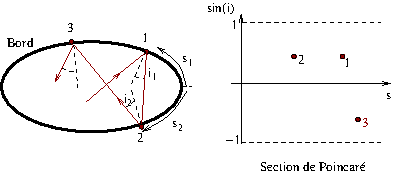
Trajectoire = Suite: ,,,
qui forme une dynamique discrète déterministe et de dimension 2. (qui conserve l'aire). Billard plus déformé :
Structure très riche observée.
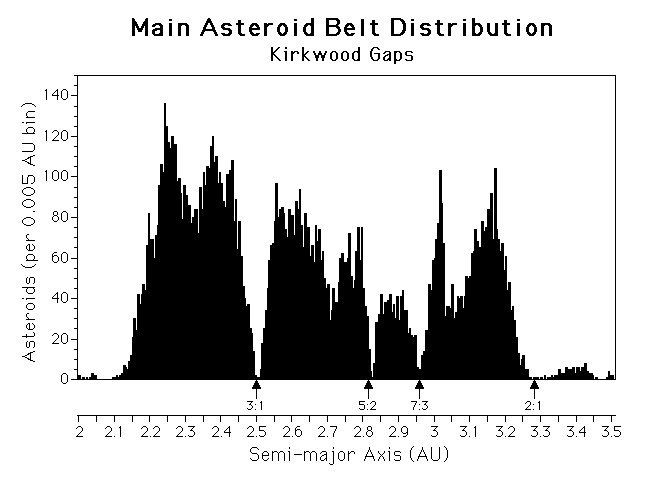
3.2.4 Des résonances dans le système solaire
Gaps observés dans la répartition des millions d'astéroïdes situés entre mars et Jupiter: gaps de Kirkwood (1866) si période telle que (A cause des instabilités voisines, ils subissent des chocs et se font éjecter).
Gaps dans les anneaux de Saturne: les cailloux de période vont être éjectés à cause des instabilités (chocs avec d'autres cailloux).
Satellites d'Uranus prédits à partir de gaps observés dans les anneaux
4 Dimension 3
4.1 Dynamique à temps continu en dimension 3
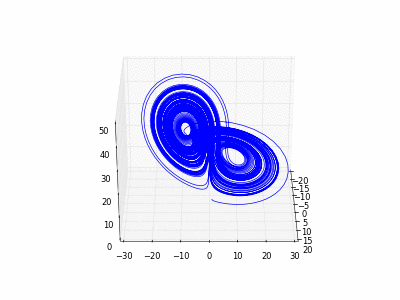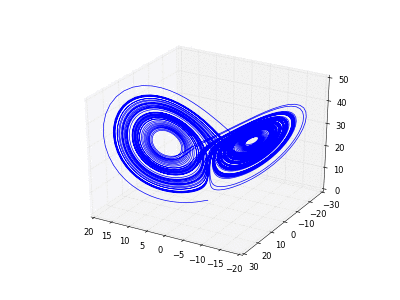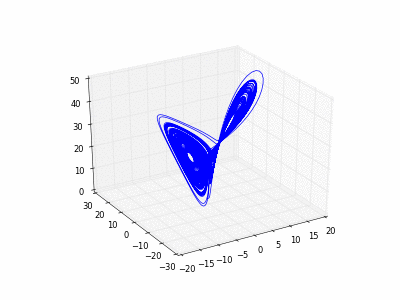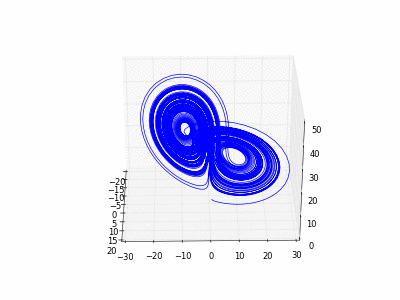
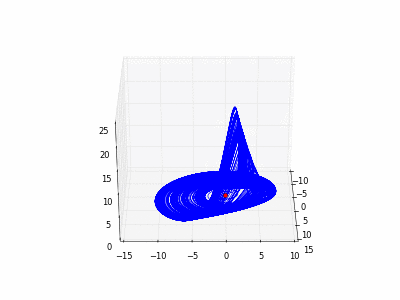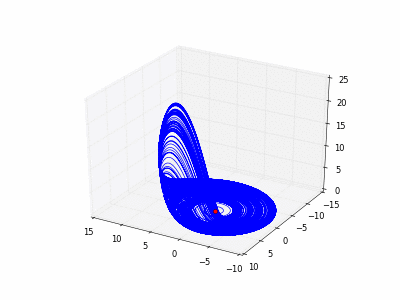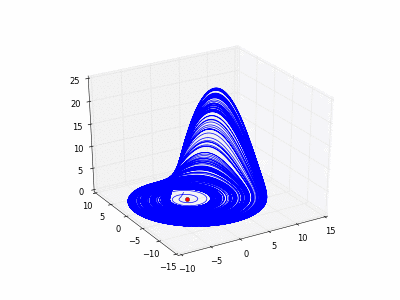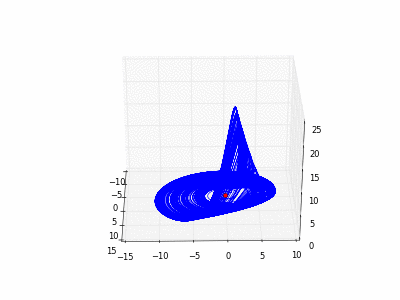
4.1.1 Exemple du « flot de Lorenz ».
On considère
qui dépend de
et qui satisfait l'équation de mouvement
avec les paramètre
. On appelle (
4.1) les
equation de Lorenz. La fonction
s'interprète comme un champ de vecteur sur
.
Références.
4.1.2 Exercices préparatoires
- Calculer et déterminer si le flot est contractif, expansif ou conservatif selon le point .
4.1.3 Exercices de programmation
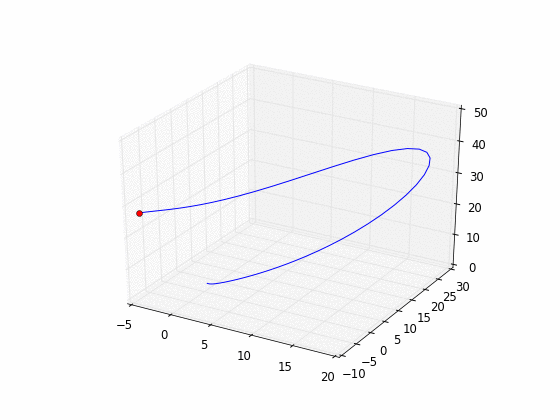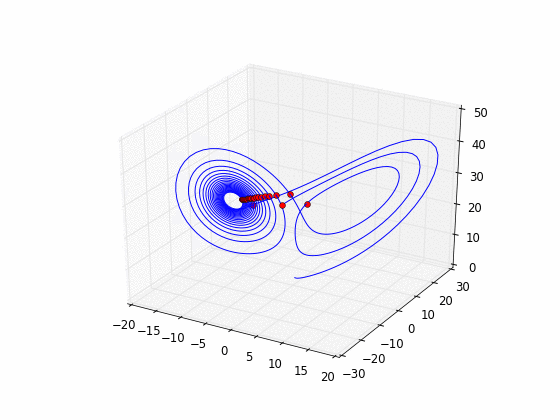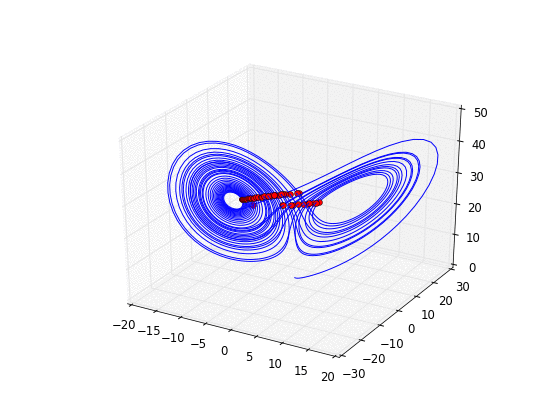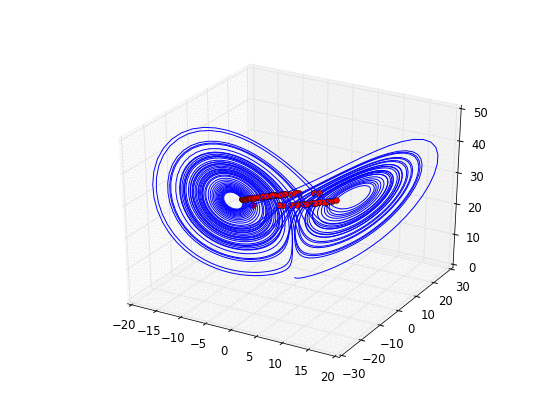
- Copier et exécuter cet exemple exemple. Faire évoluer un point rouge sur l'attracteur de Lorenz.
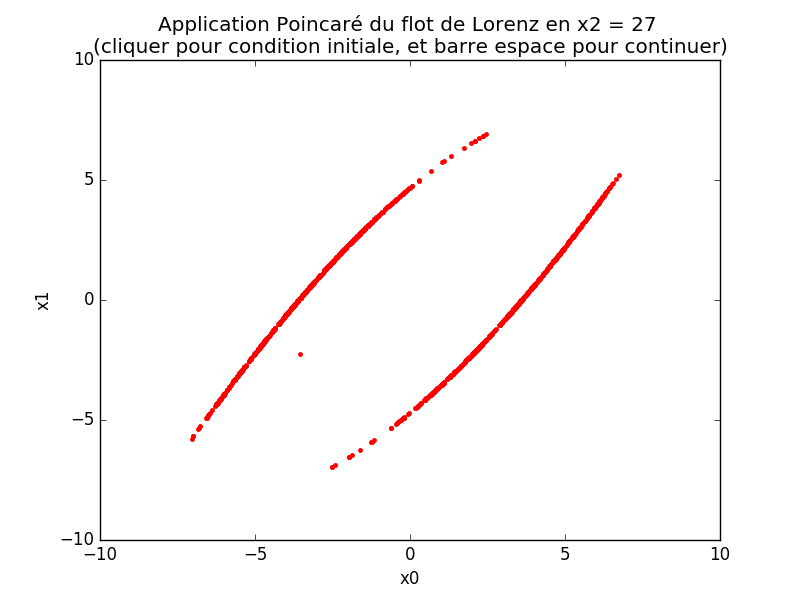
4.1.4 Section de Poincaré
- Choisir une surface (ou plan) dans l'espace appelée Section de Poincaré, par exemple , et considérer la suite des intersections de la trajectoire avec ce plan. Cela définit une dynamique de dimension 2 à temps discret, appelée Application de Poincaré du flot. Exercice: tracer la suite des intersections en 3D (point rouges sur trajectoire bleue) puis en 2D (points choisis à la souris dans la section de Poincaré). Solution: programme python
4.1.5 Autres exemples de flots en dimension 3
- « Attracteur de Rossler ». Etudier la dynamique de Rossler (changer les conditions initiales, ...). Voir sujet 2 et correction. Programme python.
- « Pendule pulsé ». Considérer un pendule de longueur variable , masse . On pose la position angulaire et . Ecrire l'équation de mouvement. Montrer que l'on obtient un champ de vecteur dans l'espace de dimension trois où avec . Tracer une section de Poincaré pour .
- Une particule dans le plan et soumis à une force dérivant d'une énergie potentielle . L'énergie est conservée et dans la couche d'énergie qui est de dimension 3, les équations de mouvement de Hamilton définissent un champ de vecteur.
Solutions
: