Introduction au cours Systèmes dynamiques, chaos et applications

Date: 1 septembre 2015

Frédéric Faure

Chapter 1 Introduction

1.1 Modèle du pendule

1.2 L'application logistique (1838, 1976)

1.3 Billard de Sinaï (1970)

1.4 Dynamique spatio-temporelle

Notice:

les "vidéos" sont des gifs animés. Si vous utilisez le navigateur Firefox, on conseille d'installer le plugin "Toggle animated GIFs" et d'utiliser les touches:
(Pour plus de fluidité, vous pouvez sauver l'image animée (gif) sur votre ordinateur et la visualiser ensuite avec Firefox. Pour plus d'options, vous pouvez utiliser le logiciel "Xanim" qui permet de visualiser la vidéo "gif animated" sur votre ordi et pouvoir changer la vitesse de lecture.)
Les animations en été crée avec un programme en C++. Si vous souhaitez utiliser/modifier ces programmes voici les codes source.

Chapter 1
Introduction

La question fondamentale en théorie des systèmes dynamiques est:

“Connaissant les lois d'évolution infinitésimale, prévoir le comportement effectif à temps longs?”

L'homme s'interroge sur cette question depuis la nuit des temps. Les premières réponses sont venues avec le mouvement des astres car assez simple et donc prévisible (les 7 objets célestes visibles: lune (lundi), mars (mardi), mercure (mercredi), jupiter (jeudi), venus (vendredi), saturne (samedi), soleil (dimanche)).

image: 0_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_rond-etoile-02.jpg

image: 1_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_mars.jpg

image: 2_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_syst_solaire2.gif

Figure 1.0.1:Mouvement apparent des etoiles, de mars. I a fallu du temps pour découvrir que la Terre appartient au système solaire.

image: 3_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_carnac.jpg

image: 4_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_eruption_solaire.jpg

Figure 1.0.2:La plupart des phénomènes observés semblent imprévisibles, car trop “complexes”, “chaotiques”. La météo échappe à la prévision au delà de quelques jours. Les éruptions solaires ont un impact sur notre climat et découlent de dynamique complexe interne au soleil. Quelle est l'origine de la complexité observée? (chaos = confusion, désordre, imprévisibilité)

Illustration de cette question avec quatre séries d'exemples:

Le pendule amorti et ses variantes. On introduit la section de Poincaré qui est une application de dimension 1 monotone donc régulière.

L'application logistique (qui est une application de dimension 1 mais non monotone donc présentant du chaos), et l'ensemble fractal de Mandelbrot qui est son diagramme de phase.

Le billard rectangulaire qui a une dynamique très simple et le billard de Sinaï qui a une dynamique très chaotique. On observe que le hasard émerge de lois déterministes.

La réaction chimique de Belousov-Zhabotinsky qui montre une “dynamique spatio-temporelle” avec “morphogénèse” (la dynamique converge vers un cycle limite, mais il semble y avoir du “chaos spatial”?).

On conseille vivement la lecture du livre (non technique)[D.Ruelle, “Hasard et chaos” 1990] et la visualisation des films “chaos” de Etienne Ghys et al.

Références:

Livre de Strogatz, “Nonlinear Dynamics and Chaos”
Livre de Cross et al. “Pattern formation”.

1.1 Modèle du pendule

Le pendule est le paradigme du système mécanique simple et prévisible.

Masse ponctuelle

m

attachée à une tige rigide de longueur fixe

l

dans un plan vertical

(x, z)

. La masse est soumise à son poids

P = m g

et une force de frottement

\vec{F} = - γ \vec{v}

opposée à la vitesse

\vec{v}

, avec

γ \geq 0

qui est le coefficient de frottement.

image: 5_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_pendule.jpg

Figure 1.1.1: Pendule

1.1.1 Equation de mouvement de Newton (1687)

La position curviligne du pendule est

l \cdot α (t)

. La loi de Newton (

\sum forces = m \cdot acceleration

) donne:

\begin{matrix} - m g sin α - γ l \dot{α} = m l \ddot{α} & (1.1.1) \end{matrix}

Il est préférable d'avoir des équations du premier ordre en temps. Posons

β (t) : = \dot{α} : vitesse, donc \dot{β} = \ddot{α}

Donc

\begin{matrix} {\begin{matrix} \dot{α} & = β = : F_{1} (α, β) \\ \dot{β} & = - \frac{g}{l} sin α - \frac{γ}{m} β = : F_{2} (α, β) \end{matrix} & (1.1.2) \end{matrix}

c'est une équation différentielle ordinaire (E.D.O).

Video:

Solution numérique obtenue par la “méthode d'Euler” expliquée ci-dessous. Les paramètres sont

g = 1, l = 1, γ = 0.2, m = 1.

image: 6_home_faure_enseignement_Systemes_dynamiques_M1_Animations_chap_intro_Animation_pendule.gif

1.1.2 Résolution numérique de l'EDO (1.1.2) par la méthode de Euler (1768)

Prenons un intervalle de temps très petit

δ t ≪ 1

et posons

t_{0} = 0, t_{1} = δ t, t_{2} = 2. δ t \dots \dots t_{n} = n . δ t \dots

α_{n} : = α (t_{n}), β_{n} : = β (t_{n})

D'après la formule de Taylor à l'ordre 1:

\begin{matrix} α_{n + 1} & = α (t_{n} + δ t) = α (t_{n}) + δ t . (\frac{d α}{d t}) (t_{n}) + O (δ t^{2}) \\ = α_{n} + F_{1} (α_{n}, β_{n}) . δ t + O (δ t^{2}) \end{matrix}

Proposition:

“Méthode de Euler”: On pose

({\tilde{α}}_{0}, {\tilde{β}}_{0}) : = (α_{0}, β_{0})

et (on oublie le reste

O (δ t^{2})

)

{\begin{matrix} {\tilde{α}}_{n + 1} & = {\tilde{α}}_{n} + F_{1} ({\tilde{α}}_{n}, {\tilde{β}}_{n}) . δ t \\ {\tilde{β}}_{n + 1} & = {\tilde{β}}_{n} + F_{2} ({\tilde{α}}_{n}, {\tilde{β}}_{n}) . δ t \end{matrix}

Alors

({\tilde{α}}_{n}, {\tilde{β}}_{n})

est une bonne approximation de la vraie position

(α_{n}, β_{n})

. En effet, l'erreur est majorée par

| {\tilde{α}}_{n} - α_{n} | \leq O (δ t^{2}) . n = O (t_{n}) . δ t ≪ 1.

image: 7_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_methode_euler.jpg

Remarque:

l'ODE est donc une loi déterministe: l'état initial

α_{0}, β_{0}

détermine

α (t), β (t)

pour tout temps

t

1.1.2.1 Variante: le pendule forcé (oscillateur entretenu)

On remplace le terme de frottement

- \frac{γ}{m} β

par

\frac{γ}{m} (β - \frac{β^{3}}{c^{2}})

qui est positif si

0 < β < c

et négatif si

β > c

image: 8_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_courbe_b-b3.jpg

Vidéo:

Trajectoire partant de la condition initiale

α_{0} = 0, β_{0} = 0.1

. L'amplitude augmente et la trajectoire converge vers un cycle limite (trajectoire périodique). Les paramètres sont

g = 1, l = 1, γ = 0.2, m = 1, c = 1.

image: 9_home_faure_enseignement_Systemes_dynamiques_M___ions_chap_intro_Animation_pendule_entretenu.gif

La trajectoire part de la condition initiale

α_{0} = 0, β_{0} = 2

et converge vers le même cycle limite:

image: 10_home_faure_enseignement_Systemes_dynamiques____ns_chap_intro_Animation_pendule_entretenu_2.gif

Remark 1.1.1. Par exemple, la voix, (vibration des cordes vocales) est un exemple d'oscillateur entretenu par le débit d'air.

1.1.3 Section de Poincaré (1892)

Définition:

La demi droite

{α = 0, β \geq 0}

s'appelle la section de Poincaré et l'application:

P : {\begin{matrix} R^{+} & \to R^{+} \\ β_{n} & \to β_{n + 1} = P (β_{n}) \end{matrix}

s'appelle l'application de Poincaré.

image: 11_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_section_poincare.jpg

image: 12_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_application_poincare.jpg

Figure 1.1.2: Section de Poincaré et application de Poincaré.

Remarques:

Intérêt de l'application de Poincaré: son étude est plus simple que celle du flot. Par exemple le point fixe

c = P (c)

est un point attractif. Cette propriété est équivalente à l'existence d'un cycle limite attractif pour le flot.

Pour le pendule, la fonction

P : R^{+} \to R^{+}

est forcément croissante, car si

β' < β

alors

P (β') < P (β)

image: 13_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_P_croissante.jpg

1.2 L'application logistique (1838, 1976)

Utile pour modéliser simplement une dynamique de population en biologie. (Pierre-François Verhulst 1838).

Ce modèle a ensuite été étudié pour ses aspects chaotiques.

En particulier son diagramme de phase appelé “ensemble de Mandelbrot”, 1985, présenté au grand public comme « l'objet mathématique le plus complexe jamais découvert », a permis de découvrir les “fractales”.

1.2.1 Définition

Définition:

Soit

μ > 0

un paramètre fixé. L'application logistique est

f : {\begin{matrix} R & \to R \\ x & \to μ x (1 - x) \end{matrix}

image: 14_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_graphe_f_logistique.jpg

Le système dynamique associé est: partant d'une condition initiale

x_{0} \in R

, on pose

x_{1} = f (x_{0}), x_{2} = f (x_{1}), \dots, x_{n + 1} = f (x_{n}), \dots

image: 15_home_faure_enseignement_Systemes_dynamiques____tions_chap_intro_Animation_trajectoire_mu_2.gif

Remarque:

On dit que c'est un système dynamique de dimension 1 car il y a une variable

x \in R

, et “à temps discret” car les points évoluent par étapes. La loi du mouvement est simplement

x_{n + 1} = f (x_{n})

. C'est une loi déterministe car la valeur de

x_{n}

à l'instant

n

et la loi

f (x)

déterminent la valeur

x_{n + 1}

à l'instant suivant

n + 1

La question est toujours la même: “prévoir la trajectoire ${(x_{n})}_{n}$ pour $n \to \infty$ ?”

1.2.2 Observations

1.2.2.1 Allure de la fonction $f (x) = μ x (1 - x)$

Les points fixes sont

x = \infty

x = 0

x = a = 1 - \frac{1}{μ}

On a

f' (x) = μ (1 - 2 x)

donc

f' (a) = μ (1 - 2 a) = μ (1 - 2 + \frac{2}{μ}) = 2 - μ

image: 16_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_derivee_f.jpg

Ainsi si

1 < μ < 3

alors

| f' (a) | < 1

donc le point fixe

x = a

est attractif pour la dynamique de

f

f' (0) = μ > 1

donc le point fixe

x = 0

est répulsif pour la dynamique de

f

1.2.2.2 Trajectoires et ensemble attracteur de $f$

Vidéo:

Dessin d'une trajectoire partant de

x_{0} = 0.1

, pour différentes valeurs de

μ

. On observe que la trajectoire converge vers un point (si

μ = 2

), ou une séquence de 2 points (si

μ = 3.3

) ou une séquence de 4 points (si

μ = 3.54

). Cet attracteur ne dépend pas du point initial. Pour

μ = 4

, la trajectoire a un comportement “chaotique” sur tout l'intervalle

[0, 1]

image: 17_home_faure_enseignement_Systemes_dynamiques____ons_chap_intro_Animation_trajectoire_mu_3_3.gif

image: 18_home_faure_enseignement_Systemes_dynamiques____ns_chap_intro_Animation_trajectoire_mu_3_54.gif

image: 19_home_faure_enseignement_Systemes_dynamiques____tions_chap_intro_Animation_trajectoire_mu_4.gif

image: 20_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_diag_phase_mu_0_4.png

image: 21_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_diag_phase_mu_3_4.png

Figure 1.2.1: Dessin de l'ensemble attracteur de

f

en fonction de

μ

. (L'image de droite détaille l'intervalle

μ \in [3, 4]

Proposition:

Le point

x = \infty

est toujours un point attractif pour la dynamique de

f

(si

μ

non nul).

Pour

μ \in [0, 4]

l'ensemble attractif de

f

sur

R

est

{\infty} \cup A

où

A \subset R

est non vide. Pour

μ > 4

, on montre que l'ensemble attractif de

f

est l'unique point

{\infty}

1.2.2.3 Ensemble de Mandelbrot(1980)

Comme

f (x) = μ x (1 - x)

est un polynome, on peut étendre le modèle aux valeurs complexes:

μ \in C, x \in C

On a vu que l'ensemble attractif de

f

est

A \cup {\infty}

avec

A \subset C

éventuellement vide.

Définition:

L' ensemble de Mandelbrot est l'ensemble des paramètres

μ

pour lesquels l'ensemble attractif

A

f

est non vide.

Ainsi l'ensemble de Mandelbrot est un “diagramme de phase” qui montre pour quels paramètres

μ

du modèle on a un ensemble attractif limite

A

D'après la remarque ci-dessus,

M

contient l'intervalle

μ \in [0, 4]

Voici une propriété pratique pour caractériser l'ensemble de Mandelbrot:

Proposition

μ

est hors de

M

si et seulement si

f^{n} (\frac{1}{2}) \underset{n \to \infty}{\to \infty}

Autrement dit le point

x = \frac{1}{2}

est attiré par l'ensemble attracteur

A

sauf si

A

est vide. Dans ce cas

x = \frac{1}{2}

est attiré par

\infty

. (noter que

x = \frac{1}{2}

est l'unique point vérifiant

f' (x) = 0

image: 22_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_Mandelbrot_1.png

image: 23_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_Mandelbrot_2.png

Figure 1.2.2: Ensemble de Mandelbrot

M

pour l'application logistique (en noir à gauche et rouge à droite). Sur la figure de droite, les couleurs sont

log τ (μ)

où

τ (μ) = max {n, t . q . | f_{μ}^{n} (\frac{1}{2}) | < 1 0^{3}}

est le “temps d'échappement”.

Avec le logiciel libre xaos (ou autre) on peut explorer le bord de l'ensemble de Mandelbrot qui est remarquable.

Videos:

μ

varie sur la ligne

I m (μ) = 0

. ainsi on peut comparer l'ensemble attracteur (bleu) aux images précédentes.

Point bleu: ensemble attracteur de

f

qui n'existe que si

μ

(point rouge) est dans l'ensemble de Mandelbrot. Point vert: ensemble répulseur de

f

image: 24_home_faure_enseignement_Systemes_dynamiques_____chap_intro_Animation_ens_repulsif_mu_1_5_5.gif

image: 25_home_faure_enseignement_Systemes_dynamiques____ations_chap_intro_Animation_Mandel_mu_1_5_5.gif

Même figure mais

μ

varie sur la ligne

I m (z) = 0.2

image: 26_home_faure_enseignement_Systemes_dynamiques____p_intro_Animation_ens_repulsif_mu_1_5_i_0_2.gif

image: 27_home_faure_enseignement_Systemes_dynamiques_____chap_intro_Animation_Mandel_mu_1_5_5_i_0_2.gif

1.3 Billard de Sinaï (1970)

Les modèles de billard sont aussi des modèles de systèmes dynamique à la fois proches de modèles physiques réalistes et relativement simples à étudier pour certains.

1.3.1 Le billard rectangulaire

Un point de position

q_{0} \in R^{2}

et vitesse initiale

v_{0} \in R^{2}

évolue dans un billard rectangulaire. La loi du mouvement est la ligne droite (vitesse constante) et rebond parfait sur les parois (c'est à dire angle de réflexion = angle d'incidence). On observe que la trajectoire dessine une figure très régulière.

image: 28_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_billard_rectangulaire.jpg

Figure 1.3.1: Billard rectangulaire

Question:

étant donnés la position initiale

q_{0}

et la vitesse initiale

v_{0}

, prédire la position

q (t)

et la vitesse

v (t)

au temps

t > 0

quelconque?

Réponse:

Par la “méthode des images ” qui est spécifique à cette géométrie rectangulaire, le problème devient simple et soluble.

image: 29_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_methode_images.jpg

Figure 1.3.2: Méthode des images: lors du rebond d'une balle sur un miroir, son image semble continuer en ligne droite. La trajectoire est donc une ligne droite se déplaçant sur l'ensemble des images du domaine initial (ici un réseau de rectangles).

image: 30_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_rebond_trait_droit.jpg

Figure 1.3.3: La méthode des images revient à “plier” et “déplier” une surface plate: on utilisera cette remarque plus loin.

1.3.2 Billard dispersif de Sinaï (1970)

Le billard de Sinaï est un carré avec conditions périodiques au bord (c'est donc un tore

T^{2}

) et contenant des disques. Une bille évolue en ligne droite à vitesse constante et rebondit parfaitement sur le bord des disques. Elle a donc un comportement déterministe. Mais on observe que le comportement est imprévisible, “chaotique”. Pourquoi?

Video:

image: 31_home_faure_enseignement_Systemes_dynamiques_M1_Animations_chap_intro_1_Animation_1_bille.gif

image: 32_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_billard__10.gif

Réponse:

L'explication heuristique est que les bords du billard sont convexes ce qui implique une “dispersion des trajectoires” après chaque rebond:

image: 33_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_rebond_billard_disque.jpg

Après quelques rebonds seulement, les deux trajectoires initialement très proches peuvent avoir des évolutions très différentes (décorrélées). Sur la figure suivante, on observe une bille avec une incertitude initiale

Δ y = 1 0^{- 4}

. Cette incertitude croit exponentiellement et le comportement peut différer après un temps très court.

image: 34_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_billard_t200.gif

La dynamique déterministe engendre donc du hasard. Cela est à l'origine du “chaos déterministe” et de la complexité dans les systèmes dynamiques, et plus généralement de la complexité en physique et dans la nature. Référence: Ruelle “Hasard et chaos” 1990.

Question:

Est-il possible de faire des prédictions sur l'évolution malgré ce hasard ? de comprendre les lois de ce hasard?

1.3.3 Approche probabiliste

Il est nécessaire d'adopter une approche probabiliste. Voici l'idée.

Observons

N = 1 0^{4}

billes indépendantes avec des conditions initiales très proches

Δ y = 1 0^{- 4}

. La distribution des billes peut s'interpréter comme une distribution de probabilité pour la bille initiale.

La distribution des billes peut s'interpréter comme une distribution de probabilité d'une bille initiale. Cette distribution converge vers l'équilibre et diffuse sur le réseau (sur le plan). On observe un comportement prédictible mais irréversible. (On introduira la notion d'entropie pour caractériser cette perte d'information sur la position de la particule au cours du temps).

image: 35_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_billard_cloud.gif

Vidéos:

image: 36_home_faure_enseignement_Systemes_dynamiques_M1_Animations_chap_intro_colors.png

image: 37_home_faure_enseignement_Systemes_dynamiques_____animation_10e6_billes_billard_et_diffusion.gif

image: 38_home_faure_enseignement_Systemes_dynamiques____hap_intro_3_Animation_10e4_billes_diffusion.gif

1.4 Dynamique spatio-temporelle

Dans les modèles précédent, la variable qui évolue au cours du temps était un point dans un espace de dimension finie:

x (t) = (α (t), β (t)) \in R^{2}

pour le pendule,

x_{n} \in R

pour l'application logistique,

(q (t), v (t)) \in R^{2} \times R^{2}

pour le billard.

Il est de nombreux problèmes de physique où la variable qui évolue est une fonction sur l'espace (une “onde” ou un “champ”), qui peut représenter en chimie la concentration d'un composé, en mécanique des fluide ce peut être le champ des vitesses, etc.

En 1952 Alan Turing écrit “The Chemical Basis of Morphogenesis” pour essayer de comprendre l'émergence de formes et structures dans la nature.

image: 39_home_faure_enseignement_Systemes_dynamiques_M1_Images_Pattern_pierres.jpg

image: 40_home_faure_enseignement_Systemes_dynamiques_M1_Images_Pattern_riviere.jpg

image: 41_home_faure_enseignement_Systemes_dynamiques_M1_Images_Pattern_riviere2.jpg

image: 42_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_dunes.jpeg

image: 43_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_pattern_leopard.jpeg

image: 44_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_galaxy_m81.jpg

image: 45_home_faure_enseignement_Systemes_dynamiques____Colonies_Dictyostelium_discoideum_BALL_1994.jpg

image: 46_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_Dictyostelium.png

Figure 1.4.1: Une évolution de bactéries Dictyostelium discoideum qui est analogue à la “réaction de Belousov-Zhabotinsky” (voir video de Florian Siegert, livre de Cross. @@)

Voir vidéos sur Youtube.

1.4.1 Modèle de Belousov-Zhabotinsky (1950)

A un instant

n \in Z

(le temps est discret)

ϕ = (ϕ_{1}, ϕ_{2}, ϕ_{3})

est une fonction à trois composantes sur le réseau

N \times N

périodisé:

image: 47_home_faure_enseignement_Systemes_dynamiques_M1_Images_chap_intro_Reseau_BZ.jpg

Pour définir

ϕ^{(n + 1)}

(à l'instant

n + 1

) à partir de

ϕ^{(n)} = ϕ

on considère deux opérations successives:

Moyennisation spatiale: c'est l'opération $\begin{matrix} (M ϕ) (x) : = \frac{1}{5} \sum_{y \in L, y \sim x} ϕ (y), \forall x & (1.4.1) \end{matrix}$ où $\sum_{y \sim x}$ signifie que la somme porte sur le point $x$ et ses 4 voisins proches.

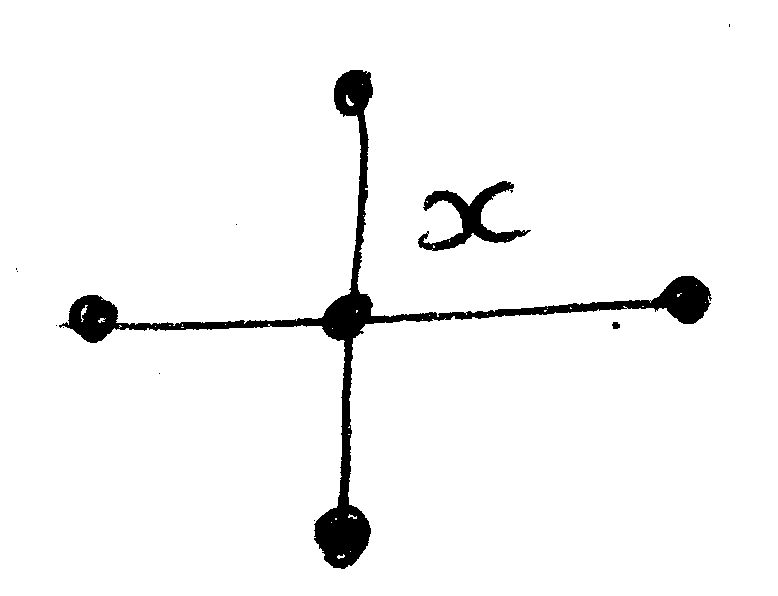
Dynamique ponctuelle sur $R^{3}$ : en chaque point $x$ du réseau, la fonction $ϕ (x) = (ϕ_{1}, ϕ_{2}, ϕ_{3}) \in R^{3}$ est modifiée par l'application: $\begin{matrix} f : {\begin{matrix} R^{3} & \to R^{3} \\ (\begin{matrix} ϕ_{1} \\ ϕ_{2} \\ ϕ_{3} \end{matrix}) & \to (\begin{matrix} ϕ'_{1} = ϕ_{1} (1 + ϕ_{2} - ϕ_{3}) \\ ϕ'_{2} = ϕ_{2} (1 + ϕ_{3} - ϕ_{1}) \\ ϕ'_{3} = ϕ_{3} (1 + ϕ_{1} - ϕ_{2}) \end{matrix}) \end{matrix} & (1.4.2) \end{matrix}$ et ensuite on restreint chaque valeur $ϕ'_{j}$ à l'intervalle $[0, 1]$ .

Vidéos:

Partant d'une fonction initiale

ϕ

tirée au hasard, on observe une convergence vers une trajectoire périodique (cycle limite) avec une structure spatiale en spirales.

image: 49_home_faure_enseignement_Systemes_dynamiques_M1_Animations_chap_intro_Animation_BZ_1.gif

Images aux périodes

T = 12

, afin de montrer la convergence vers un cycle limite:

image: 50_home_faure_enseignement_Systemes_dynamiques_M1_Animations_chap_intro_Animation_BZ_2.gif

1.4.2 Interprétation du modèle en chimie

ϕ_{1}, ϕ_{2}, ϕ_{3} \in [0, 1]

représentent les concentrations de 3 composés. On suppose qu'il y a les 3 réactions chimiques suivantes

\begin{matrix} (1) ϕ_{1} + ϕ_{2} & \to 2 ϕ_{1} \\ (2) ϕ_{2} + ϕ_{3} & \to 2 ϕ_{2} \\ (3) ϕ_{3} + ϕ_{1} & \to 2 ϕ_{3} \end{matrix}

Dans la réaction (1) on dit que

ϕ_{2}

est un catalyseur pour la création du composé

ϕ_{1}

., etc. Cela implique que à chaque étape, la variation de concentration est donnée par

\begin{matrix} Δ ϕ_{1} & = \underset{(1)}{\underset{⏟}{ϕ_{1} ϕ_{2}}} - \underset{(3)}{\underset{⏟}{ϕ_{1} ϕ_{3}}} = ϕ_{1} (ϕ_{2} - ϕ_{3}) \\ Δ ϕ_{2} & = \underset{(2)}{\underset{⏟}{ϕ_{3} ϕ_{2}}} - \underset{(1)}{\underset{⏟}{ϕ_{1} ϕ_{2}}} = ϕ_{2} (ϕ_{3} - ϕ_{1}) \\ Δ ϕ_{3} & = \underset{(3)}{\underset{⏟}{ϕ_{1} ϕ_{3}}} - \underset{(2)}{\underset{⏟}{ϕ_{2} ϕ_{3}}} = ϕ_{1} (ϕ_{2} - ϕ_{3}) \end{matrix}

donnant la loi de transformation (1.4.2). Il y a aussi diffusion spatiale des réactifs modélisée par la formule de moyennisation spatiale (1.4.1).

Table of Contents

1.1.2 Résolution numérique de l'EDO (1.1.2) par la méthode de Euler (1768)

1.2 L'application logistique (1838, 1976)

1.2.2.3 Ensemble de Mandelbrot(1980)