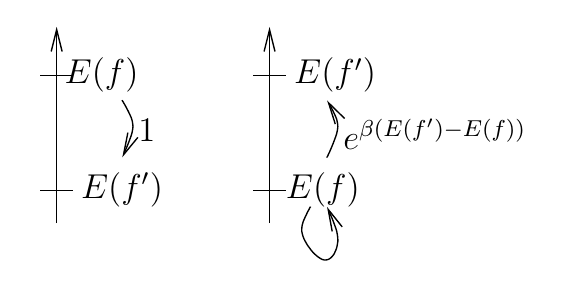Bases de programmation scientifique avec le langage Python.
Frédéric Faure
Université Grenoble Alpes, France
(version: 15 avril 2022)
Attention: Pour lire ce document, utiliser Firefox qui donne un bon rendu des équations.
Introduction
0.1 Déroulement des 10 séances en Licence L3 de physique, 2018-2019
- Pendant 3 séances, « Apprentissage du langage python ».
- Suivre ce document didacticiel Partie I “Bases du langage python”, en binome ou seul. Il faut tout lire.
- Optionnellement installer python sur votre ordinateur portable personnel.
- Faire tous les exercices demandés.
- Les parties appelées “suppléments” peuvent être lues rapidement (ou sautées en première lecture).
- En option, suivre le didacticiel Partie II “Compléments du langage python”.
- Pendant 2 séances,« 4 micro-projets »
- chaque étudiant réalise 4 (ou 5) micro-projets: 2 micro-projets par séance.
- Pour chaque micro-projet, rédiger un compte rendu de 2 ou 3 pages avec lyx, avec des images et des formules. Exporter en pdf et en xhtml et le montrer à l'enseignant, avec un oral individuel de 5mn-10mn.
- Pour apprendre Lyx, voici un document en pdf qui sert d'exemple et d'exercice. Voici le même document en html, qui vous servira éventuellement pour copier/coller.
- Pendant 5 séances « Un projet par binôme ou seul ». Attention de bien choisir son binôme: le travail devra être bien partagé et si le niveau en informatique est différent dans le binome, il faut que ce soit profitable à chacun.
- choisir un projet d'expérimentation numérique. Voir la page projets. Choisir un projet marqué (*), ce qui signifie qu'il y a un bon énoncé.
- A la dernière séance chaque étudiant (ou binome) présente son projet sur vidéo projecteur, pendant 15 à 20 mn, à l'ensemble de la classe.
- Cette présentation devra être préparée avec Lyx (qui permet de créer des documents scientifiques) et exportée en html (avec LyxHtml) et en pdf.
- Pour apprendre Lyx, voici un document en pdf qui sert d'exemple et d'exercice. Voici le même document en html, qui vous servira éventuellement pour copier/coller.
0.2 Des références générales sur python
Voici des références pour compléter ce didacticiel (qui est d'ailleurs construit à partir de ces références).
Sur internet:
Des MOOC
Livres (téléchargeables en version pdf):
0.3 Installation de Python sur votre ordinateur
On conseille d’installer
python3 et l'environnement de programmation
spyder.ainsi que les librairies scientifiques.
Par exemple utiliser la distribution
Anaconda0.3.0.1 Sur Linux, Ubuntu (recommandé)
Commandes dans un terminal:
sudo apt install python3-pip python3-dev
sudo apt install spyder
0.3.0.2 Sur Windows
0.3.0.3 Sur Mac-Os
0.3.0.4 Sur Android
0.3.0.5 En général sur un navigateur
0.4 Utilisation de python avec le logiciel « spyder »
Lancement du logiciel spyder:
dans un terminal, lancer: spyder (ou spyder3)
Il apparaît un environnement de programmation pour le langage python appelé « spyder ».
premiers Tests à faire:
- « python en mode interactif »:
- En bas à droite, dans la fenêtre « Console IPython » écrire 2+2 et entrée. Il apparait le résultat: 4.
- Pour écrire deux lignes d'instructions consécutives, il faut utiliser ctrl-entrée. Ecrire:
x=2
print (x+2)
et pour terminer tapez « entrée, entrée ». Il apparaît le résultat: 4.
- Exemple plus ludique: dans la fenêtre « Console IPython » copier/coller le texte suivant (qui sera expliqué plus tard dans ce cours):
%matplotlib inline
from pylab import *
from numpy import *
X = arange(0, 6, 0.2) # crée une liste de nombres Xi de 0 à 6 (exclu) par pas de 0.2
Y = sin(X) # cree une liste où chaque élément est Yi = sin ( Xi )
plot(X,Y) # dessin des valeurs de Yi en fonction des Xi
xlabel('x') # rajoute titre aux axes
ylabel('y=sin(x)')
show() # montre le dessin
Résultat:
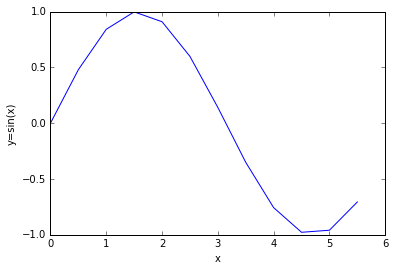
a
- « python en mode programme »: Dans la fenêtre de gauche qui est un éditeur ordinaire, et qui édite le fichier « temp.py », rajouter les lignes:
x=2
print (x+2)
et exécuter le programme par Menu/Execution (F5). Il apparaît le résultat dans la console: 4
Programmes avec graphisme:
dans ce cas il est conseillé dans spyder dans le menu Outils/Préférences/ConsoleIPython/Graphiques/Sortie : de choisir le mode automatique.
(et relancer la fenetre IPython)
0.4.1 Lancement de votre programme python dans une fenêtre de commandes
Voici comment éxecuter votre programme temp.py ci-dessus dans une fenêtre de commandes.
- Ouvrir un terminal (fenêtre de commandes)
- Aller dans le répertoire qui contient votre programme temp.py
- Ecrire:
python3 temp.py
Dans la suite de ce didacticiel, vous pourrez écrire les lignes de codes proposées en mode interactif ou en mode programme. Pour recopier le(s) code(s) proposé(s), vous pouvez faire « copier/coller ».
0.5 (supplément) Utilisation de python avec le logiciel « Jupyter »
Si vous avez choisit de travailler avec « spyder » comme ci-dessous, vous pouvez ignorer cette Section.
Lancement du logiciel Jupyter
- dans un terminal, lancer: anaconda-navigator
- Cliquer sur « Launch JupyterLab ». Il apparaît un environnement de programmation pour le langage python appelé « JupyterLab ».
- Cliquer sur l'icone « NoteBook/Python3 »
Mode commandes: si le bord est bleu.
- Touches: a: crée entrée au dessus, b: crée entrée dessous, dd: détruit l'entrée. Entrée: passe en mode éditeur.
Mode éditeur: si le bord est vert.
- touche escape: passe en mode commandes.
0.6 (supplément) Utilisation de python en ligne
avec le site Colaboratory de google:
0.7 Utilisation de commandes dans un terminal
Si vous avez une question sur l'utilisation de ubuntu, par exemple comment ouvrir et utiliser un terminal, écrire dans google: “ubuntu terminal”.
Dans ubuntu, ouvrir une fenêtre de commandes (ou terminal). Dans cette fenêtre de commandes, vous pouvez écrire des commandes à l'ordinateur. Ces commandes sont dans le langage UNIX, système avec lequel fonctionne l'ordinateur. Cette section vous explique les principales commandes de UNIX qu'il faut connaître: les commandes qui permettent de gérer l'emplacement et le nom de vos fichiers (qui seront par exemples vos programmes en python).
Il est important de savoir que les fichiers sont classés dans l'ordinateur (sur le disque magnétique) selon une structure arborescente. Chaque noeud de l'arborescence s'appelle un répertoire ou dossier ou directory (en anglais). Dans ces répertoires se trouvent des fichiers (ou file en anglais).
Par exemple /h/moore/u4/phyliphrec/aaal/toto.py signifie que le fichier toto.py se trouve dans le répertoire aaal qui se trouve lui même dans le répertoire phyliphrec, qui se trouve lui même dans ...
0.7.1 Les répertoires
- Pour connaître le répertoire de votre fenêtre de commande (le répertoire courant): pwd
sur la figure suivante par exemple, le répertoire courant est /home/faure
- Pour afficher la liste des fichiers et des sous répertoires du répertoire courant: ls ou ls -als (pour avoir plus de détails)
- Pour changer de répertoire:
- pour aller dans le sous répertoire appelé rep: cd rep
- pour aller dans le répertoire parent: cd ..
- pour revenir à votre répertoire d'origine: cd ou cd ~
- Pour créer un sous répertoire appelé rep: mkdir rep
- Pour détruire un sous répertoire appelé rep: rm -r rep
0.7.2 Exercices sur les répertoires
A l'aide des commandes expliquées ci-dessus:
- Placez vous dans votre répertoire d'origine: cd
- Vérifiez que vous y êtes bien: pwd
- Regardez la liste des fichiers par: ls , puis avec: ls -als
- Créer un répertoire du nom: essai Vérifier son existence (avec ls).
- Aller dans ce répertoire: cd essai Vérifier que vous y êtes (avec pwd).
- Revenir dans le répertoire d'origine par cd .. Vérifiez que vous y etes. Détruire le répertoire essai
0.7.3 Les fichiers (en exercice)
- Créer un nouveau fichier avec l'éditeur emacs: emacs fichier.txt &
écrire le texte: salut
Menu: File/Save
Menu: File/Quit
On vérifie le contenu du fichier dans la fenêtre de commandes: more fichier.txt
- Pour changer le nom du fichier.txt en fichier2.txt: mv fichier.txt fichier2.txt
- Pour déplacer le fichier2.txt dans le sous répertoire rep:
mkdir rep
mv fichier2.txt rep/fichier3.txt
- Pour copier le fichier3.txt dans le répertoire parent:
cd rep
cp fichier3.txt ../fichier1.txt
- Pour détruire le(s) fichiers:
rm fichier3.txt
cd ..
rm fichier1.txt
rm -r rep
0.7.4 La documentation sur les commandes unix
- Pour avoir la documentation sur la commande ls par exemple, taper dans une fenetre de commande: man ls
- Voici une documentation sur les commandes possibles bash pour la fenêtre terminal.
Partie I
Bases du langage python
Chapitre 1 Objets de bases
1.1 Nombres entiers et nombres à virgule. Entrée et sortie à l'écran.
Pour créer une variable, il suffit de lui affecter une valeur. Le texte après le symbole # est un commentaire et est ignoré par l'ordinateur. Ecrire:
x = 1 # met le chiffre 1 dans la variable x
print (x)
résultat:
1
On voit ici une différence importante avec d'autres langages : il n'est pas nécessaire de déclarer a priori le type de la variable x (entier 'int' (integer), nombre flottant 'float', chaine de caractère 'string',...). Pourtant ce type existe bien, si vous écrivez ensuite :
print (type(x))
résultat:
<type 'int'>
Python a donc automatiquement décidé que x était un entier (int = integer). Ré-essayez avec d'autres initialisations : x=1.0 (nombre à virgule flottante ou float), ou x = 'bonjour' (chaine de caractère ou string),...
On peut affecter plusieurs variables à la fois. Ecrire:
x,y = 1, 2
print (x,y)
résultat:
1 2
ou écrire:
x = y = 1
print (x)
print (y)
résultat:
1
1
Remarque: dans l'exemple précédent, pour que les deux résultats soient sur la même ligne (sans saut de ligne), il faut rajouter ,end=' ' à la fin de la première ligne. Ecrire:
x = y = 1
print (x,end=' ')
print (y)
résultat:
1 1
Pour demander à l'utilisateur le contenu d'une variable, écrire:
x = input('x=? ') # demande un nombre et le met dans la variable x
print (x)
print (type(x))
y = int(x) # convertit x qui est de type 'str' en type 'int'
print (y)
print (type(y))
résultat:
x=? 2
2
<type 'str'>
2
<type 'int'>
Attention : majuscules et minuscules sont différenciées par python, i.e. ma_variable, MA_VARIABLE et Ma_Variable sont trois variables distinctes. Ecrire:
ma_variable = 1
Ma_variable = 2
print (ma_variable)
résultat:
1
Pour que la console oublie la valeur de x (et de toutes les variables) il faut écrire: %reset
1.2
Chaînes de caractères
Une chaine de caractère est un tableau contenant des caractères. On peut ainsi construire des mots et des phrases et les manipuler. La numérotation des « cases » commence à zéro.
Ecrire:
nom='Vincent'
print (nom)
print (nom[2:6]) # extrait les caractères 2 (inclus) à 6 (exclu),
Résultat:
Vincent
ncen
Il est possible d'additionner des chaînes de caractères. Ecrire:
print ('Programmation' + ' Scientifique')
résultat:
Programmation Scientifique
On peut obtenir la longueur d'une chaîne de caractère avec la fonction len(). Ecrire:
len('toto')
résultat:
4
1.2.1 Formatage
Référence:
Il est possible d'écrire une chaîne de caractère en insérant des codes spécifiques dans la chaîne (de la même manière qu'avec la fonction printf en langage ): (%s pour une chaîne de caractères, %d pour un entier, %f pour un nombre à virgule, et optionellement le nombre de caractères total et après la virgule: %4.2f veut dire 'nombre représenté sur 4 caractères, avec 2 chiffres après la virgule'), suivie de % avec entre parenthèses toutes les variables dont les valeurs sont à insérer. Ecrire:
age=5
nom="Vincent"
taille=1.73
maChaine="%s a %d ans et mesure %4.2f m" % (nom,age,taille)
print (maChaine)
résultat:
Vincent a 5 ans et mesure 1.73 m
Pour avoir la liste des fonctions utilisables avec des chaînes de caractères, écrire:
help(str)
1.3 Conversion de variables entre différents types
On peut convertir une variable d'un type à un autre. Ecrire:
x=float(1) # nombre réel à partir d'un entier
print (type(x))
résultat:
<type 'float'>
Ecrire:
x=float('1.0') # nombre réel à partir d'une chaîne de caractère
print (type(x))
résultat:
<type 'float'>
Ecrire:
print (x)
résultat:
1.0
Exercice 1.3.1.
Ecrire un programme qui demande le nom et l'âge d'une personne. En retour elle affiche l'année de naissance. Par exemple:
ton nom=? blaise
ton age=? 25
Salut blaise , tu es né en 1993 ?
1.4 Opérations mathématiques
1.4.1 opérations de base
1.4.1.1 Opération de division et puissance
écrire:
print (7/2, 7//2, 3**2)
résultat:
3.5 3 9
Noter que la première opération / a donné la division décimale et la deuxième opération // a donné la division Euclidienne (le résultat est un entier).
1.4.1.2 Modulo
Le « modulo »: n%q est le reste de la division euclidienne de par :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ecrire:
print (4%3, -1%3) # 4 modulo 3, (-1) modulo 3
print (7.5%3.0, -2.5%3.0) # 7.5 modulo 3.0, (-2.5) modulo 3.0
résultat:
1 2
1.5 0.5
1.4.1.3 Fonctions mathématiques
Pour calculer une racine carrée: (le texte après le signe # est un commentaire)
from math import * # cela importe le module math
sqrt(2.)
résultat:
1.4142135623730951
Pour avoir la liste des fonctions mathématiques disponibles écrire
help()
math
Remarque : pour importer un module (tel que math), il y a deux manières de le faire, avec (a) “import math” ou (b) “from math import *”. Dans le cas (a), les fonctions du module math s'utiliseront en les faisant précéder de “math.” (exemple : “math.sin(math.pi/3.0)”). Dans le cas (b), il n'est pas nécessaire d'utiliser le préfixe, i.e. python comprendra directement “sin(pi/3.0)”. A priori, la première notation n'est à utiliser que si il y a un risque de conflit de noms entre fonctions, si par exemple vous souhaitez redéfinir par ailleurs la fonction sin().
1.4.2 Nombre aléatoire
Pour choisir un nombre à virgule au hasard entre 0 et 1, écrire:
import random
x = random.random()
print (x)
résultat:
0.9565461152605507
Pour choisir au hasard un nombre entier entre 1 et 6 compris, écrire:
import random
x = random.randint(1, 6)
print (x)
Résultat:
3
Exercice 1.4.1.
Ecrire un programme qui demande un nombre entier x à l'utilisateur et en retour affiche un entier choisit au hasard entre 0 et x. On souhaite le résultat:
x=? 3
2
Solution:
import random
x = input('x=? ')
print random.randint(0, x)
1.4.3 Nombres complexes
Il est possible de manipuler des nombres complexes en Python, le nombre complexe étant noté 1j . Ecrire:
a=2+1j
type(a)
résultat
<type 'complex'>
Ecrire
b=3.5+4j
print (a+b)
résultat
(5.5+5j)
Ecrire
print (a*b)
résultat:
(3+11.5j)
Pour utiliser des fonctions mathématiques sur des complexes, il faut importer le module cmath en plus du module math. Par exemple pour calculer qui est égal à , écrire:
from math import *
from cmath import *
print (exp(1j*pi))
résultat:
(-1+1.2246467991473532e-16j)
1.4.4 (supplément) Nombre en base 2, binaire.
Les 2 symboles utilisés en base 2 sont: . Pour indiquer qu'un nombre est écrit en base 2, on précède son écriture du symbole 0b.
Ecrire:
#... Declaration et Affichage en base deux:
A=0b1001 # declaration en base 2 (prefixe 0b)
print 'A=' , A , ' en binaire = ' , bin(A)
#.. decalages de bits
b= A<<4 # equivalent: b= A * (2**4)
print ' b =', b, ' = ', bin(b)
c = b>>3 # equivalent: c= b / (2**3)
print ' c =', c, ' = ', bin(c)
#.. operations bits a bits
B = 0b1;
d = A | B # ou inclusif bit a bit cad 1|1 donne 1
e = A ^ B # ou exclusif bit a bit cad 1^1 donne 0
f = A & B # et bit a bit
g = ~A # non A, inversion des bits
print ' B=', B, ' = ', bin(B)
print ' A|B = ', d, ' = ', bin(d)
print ' A^B = ', e, ' = ', bin(e)
print ' A&B = ', f, ' = ', bin(f)
print ' ~A = ', g, ' = ', bin(g)
Résultats:
A= 9 en binaire = 0b1001
b = 144 = 0b10010000
c = 18 = 0b10010
B= 1 = 0b1
A|B = 9 = 0b1001
A^B = 8 = 0b1000
A&B = 1 = 0b1
~A = -10 = -0b1010
1.4.5 (supplément) Nombre en base 16 (hexadécimale)
Les 16 symboles utilisés en base 16 sont: . Pour indiquer qu'un nombre est écrit en base 16, on précède son écriture du symbole 0x. Ecrire:
nombre = 0xb # déclaration en base 16
print (nombre) # affichage en base 10
Résultat (écriture en base 10):
11
1.5 Listes
Un type particulièrement intéressant est la
liste qui permet de construire et manipuler une liste d'objets divers. Référence sur le type
list.
Ecrire:
ma_liste = [1,4, 'ABC']
print (ma_liste)
résultat:
[1, 4, 'ABC']
Ecrire:
ma_liste = [1,4, 'ABC']
print (ma_liste[2])
résultat:
ABC
Ecrire:
ma_liste = [1,4, 'ABC']
print (type(ma_liste))
print (type(ma_liste[2]))
résultat:
<type 'list'>
<type 'str'>
1.5.1 Opérations sur les listes
Il est possible de modifier une liste existante. Ecrire (le texte après le signe # est un commentaire)
L = [1,3,7,5]
L[1]=42 # le 2ème élément de MaListe vaut maintenant 42
print ('L1=', L)
L.append(45) # ajoute l'objet “45” à la fin de la liste
print ('L2=', L)
L.insert(2, 33) # insère (rajoute) l'élément 33 à l'indice 2 dans MaListe
print ('L3=', L)
del L[1] # enleve element de la case 1
print ('L3a=', L)
res = L.pop(1) # enleve element de la case 1 et le donne
print ('L3b=', L, ' res=',res)
L.remove(45) # enleve le premiere element trouve egal a 45
print ('L3c=', L)
L.reverse() # inverse l'ordre des éléments de la liste
print ('L4=', L)
L.sort() # trie les éléments de la liste par ordre croissant
print ('L5=', L)
L2 = [] # cree une liste vide
print ('L6=', L2)
L3 = list(L) # copie dans une autre liste
L3[0] = 0
L4 = L # ce n'est pas une vraie copie: liste4 est le meme objet que MaListe
L4[0] = -1
print ('L7=', L3)
print ('L8=', L)
résultat:
L1= [1, 42, 7, 5]
L2= [1, 42, 7, 5, 45]
L3= [1, 42, 33, 7, 5, 45]
L3a= [1, 33, 7, 5, 45]
L3b= [1, 7, 5, 45] res= 33
L3c= [1, 7, 5]
L4= [5, 7, 1]
L5= [1, 5, 7]
L6= []
L7= [0, 5, 7]
L8= [-1, 5, 7]
On peut obtenir la longueur d'une liste (le nombre d'objets dans la liste) avec la fonction len():
MaListe = [1,3,7,5]
len(MaListe)
résultat:
4
Il est possible de concaténer deux listes avec l'opérateur + :
liste1 = [1,'ab',3.5]
liste2 = ['toto',57]
print (liste1 + liste2)
résultat:
[1, 'ab', 3.5, 'toto', 57]
On peut également supprimer un élément d'une liste avec la fonction del() :
MaListe=[1, 'ab', 3.5, 'toto', 57]
print (MaListe)
del(MaListe[1])
print (MaListe)
résultat:
[1, 'ab', 3.5, 'toto', 57]
[1, 3.5, 'toto', 57]
Pour créer des listes particulières de nombres:
range(2,7) # liste des entiers consécutifs de 2 (inclu) à 7 (exclu)
résultat:
[2, 3, 4, 5, 6]
Si on commence de 0 il est plus simple d'écrire:
range(7) # liste de 0 (inclu) à 7 (exclu)
résultat:
[0, 1, 2, 3, 4, 5, 6]
Les listes sont des objets particulièrement utiles. Nous verrons que les boucles utilisent souvent une itération sur des éléments d'une liste. La liste complète des fonctions utilisables pour une liste peut être obtenue avec l'aide help(list).
1.5.2 Listes et hasard
Pour choisir au hasard un élément parmi une liste donnée, écrire:
import random
x = random.choice(['a', 'b', 'k', 'p', 'i', 'w', 'z'])
print (x)
Résultat:
'k'
Pour mélanger au hasard une liste donnée écrire:
import random
liste = ['a', 'b', 'k', 'p', 'i', 'w', 'z']
random.shuffle(liste)
print (liste)
résultat:
['p', 'k', 'w', 'z', 'i', 'b', 'a']
Exercice 1.5.2.
Ecrire un programme qui choisit au hasard un élément parmi une liste donnée, comme le programme ci-dessus, mais en utilisant les fonction len() et random.randint().
Solution:
import random
liste = ['a', 'b', 'k', 'p', 'i', 'w', 'z']
print (liste[random.randint(0,len(liste)-1)])
1.6 Boucles et opérateurs
1.6.1 opérateurs ==, and, or , not
L'opérateur == permet de comparer deux objets. Ecrire:
1==2 # est-ce que 1 est égal à 2 ?
1==1
résultat:
False
True
Les autres opérateurs de comparaison sont <, >, <=, >=,!= (ce dernier signifie différent). Par convention, l'entier correspond à False et les entiers non nuls correspondent à True.
L'opérateur not(x) renvoie la négation (au sens booléen, vrai/faux) d'une expression :
not(True)
not(False)
not(0)
résultat:
False
True
True
and et or permettent de réaliser les opérations logiques usuelles (attention il ne s'agit pas d'opérations bit à bit, il ne faut donc utiliser and et or que pour des tests booléens vrai/faux):
1 and 0
1 and 1
1 or 0
résultat:
0
1
1
1.6.2 L'instruction if...elif..else
On peut exécuter une instruction conditionnelle avec if. Écrire:
x=1
print ('x=',x)
if x==2: # est-ce que x est égal à 2 ?
print ('x est égal à 2') # notez les espaces en début de ligne (indentation)
elif x==3:
print ('x est égal à 3')
else:
print ("x n'est pas égal à 2")
print ('ni à 3')
résultat:
x=1
x n'est pas égal à 2
ni à 3
Les espaces en début de ligne (indentation) jouent un rôle important : tant que l'espace reste le même en début de ligne, on reste dans le même “niveau” d'éxécution, de même que dans d'autres langages on utilise des accolades {} pour délimiter les instructions à réaliser. On peut ainsi réaliser des instructions imbriquées en augmentant le niveau d'indentation :
x=12
if (x%2)==0: # est-ce que x modulo 2 est égal à 0 ?
if (x%3)==0:
if (x%7)==0:
print ('x est multiple de 2,3 et 7 !')
else:
print ('x est multiple de 2 et 3, mais pas de 7...')
else:
print ('x est multiple de 2 mais pas de 3')
else:
print ('x n'est pas multiple de 2')
résultat:
x est multiple de 2 et 3, mais pas de 7...
1.6.3 La boucle while
On peut réaliser une série d'instructions tant qu'une condition est réalisée :
x=7
while x>=1:
print (x,'>=1 ! On continue...')
x = x-1 # on pourrait aussi écrire x -= 1
résultat:
7 >=1 ! On continue...
6 >=1 ! On continue...
5 >=1 ! On continue...
4 >=1 ! On continue...
3 >=1 ! On continue...
2 >=1 ! On continue...
1 >=1 ! On continue...
1.6.4 Les boucles for
Une boucle for s'écrit de la manière suivante :
for i in [2,3,7]: # De manière générale : for variable in liste:
print (i)
résultat:
2
3
7
Comme il est fastidieux d'écrire un grand nombre de valeurs, on peut utiliser la fonction range() qui renvoie une liste d'entiers consécutifs:
for i in range(2,5):
print i
résultat:
2
3
4
Remarque: range(5) est équivalent de range(0,5)
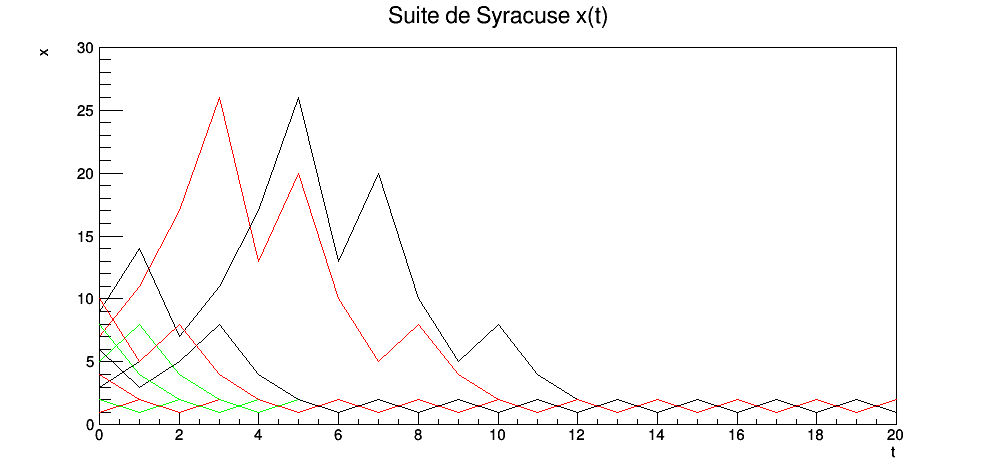
Exercice 1.6.2.
« La Suite de Syracuse ». Soit un nombre entier
. Par récurrence, on définit
à partir de
par:
Observer que la valeur de départ donne la suite infinie périodique
La valeur de départ donne la suite
La fameuse
conjecture de Syracuse non démontrée à ce jour est que partant de toute valeur
la suite arrive forcément au bout d'une date
(qui dépend de
) à la suite périodique
Ecrire un programme qui demande à l'utilisateur et affiche les valeurs de la suite jusqu'à ce que la valeur soit atteinte. Exemple de résultat:
x0=?7
11 , 17 , 26 , 13 , 20 , 10 , 5 , 8 , 4 , 2 , 1 ,
Solution:
x0 = int(input('x0=?'))
while(x0 != 1):
if(x0%2 == 0):
x0=x0/2
else:
x0=(3*x0+1)/2
print (x0,',',end=' ')1.7 Mesurer le temps
Ecrire:
from numpy import *
import time
t0 = time.time() # mesure de la date actuelle
for p in range(100000): # un calcul quelconque
y = cos(p)
t1 = time.time() # mesure de la date
print ('Duree: t1-t0 = %6.3f s' %(t1-t0)) # affiche (t1-t0) avec une précision de 3 chiffres après la virgule, voir section 1.2
résultat:
Duree: t1-t0 = 0.116 s
1.8 Fonctions
Nous avons déjà utilisé les fonctions print() et type(). De manière générale, une fonction appelée f et prenant des paramètres x,y s'utilise de la manière suivante : f(x,y) ou (si la fonction renvoie une valeur y) : y=f(x,y)
Pour définir une nouvelle fonction, il faut utiliser le mot-clef “def”.
Ecrire
def MaFonction(nom,age): #definition de la fonction
print nom,'a',age,'ans' #noter les espaces en début de ligne
MaFonction('Obélix',5) #utilisation de la fonction
résultat:
Obélix a 5 ans
nom et age sont les paramètres de la fonction. On peut appeler la même fonction ci-dessus en utilisant une chaine de caractères pour age. Ecrire
MaFonction('Obélix','cinq') #utilisation de la fonction
résultat:
Obélix a cinq ans
Il faut que les types des paramètres fournis à la fonction soient conforme à l'utilisation qui va être faite. Ecrire
def Addition(a,b):
return a+b # Renvoie une valeur avec “return”
print Addition(1,2) #deux entiers
print Addition(1,3.0) #un entier plus un flottant= un flottant
print Addition('tata','toto') # deux chaînes de caractères
résultat:
3
4.0
tatatoto
Ecrire
print Addition(1,'toto') # entier+chaîne de caractères = erreur !
résultat:
Traceback (most recent call last):
File '<stdin>', line 1, in ?
File '<stdin>', line 2, in Addition
TypeError: unsupported operand type(s) for +: 'int' and 'str'
1.8.1 Portée des objets : variables locales et globales
En python, les variables sont locales (par défaut), ce qui signifie qu'elles n'existent qu'au niveau où elles ont été définies.
Ecrire
x=12.3 # Première variable “x”
def fonction1(): # déclaration d'une fonction
x=1 # Deuxième variable “x”
print 'Etape 1, x=',x
def fonction2(): # déclaration d'une fonction
x='Toto' # Troisième variable “x”
print 'Etape 2, x=',x
print 'Etape 0, x=',x
fonction1()
fonction2()
résultat:
Etape 0, x= 12.3
Etape 1, x= 1
Etape 2, x= Toto
Dans l'exemple ci-dessus, les 3 variables ont le même nom mais sont complètement indépendantes. On dit qu'elles sont locales. Il est à noter qu'avec un niveau d'indentation on a accès aux variables du niveau supérieur en lecture, mais on ne peut pas les modifier (contrairement au C/C++ où on peut les lire et les modifier). Essayer par exemple :
compte=0
def compteur():
print (compte)
compte = compte + 1
return compte
compteur()
résultat:
0
Traceback (most recent call last):
File "<stdin>", line 1, in ?
File "<stdin>", line 2, in compteur
UnboundLocalError: local variable 'compte' referenced before assignment
Pour pouvoir utiliser (modifier) une variable à différents endroits (autrement qu'en la passant comme paramètre à une fonction), il faut utiliser le mot-clef global :
compte=0
def compteur():
global compte
compte = compte + 1
return compte
print (compteur())
résultat:
1
Note : en général, il vaut mieux éviter d'utiliser des variables globales, et plutôt passer des variables par paramètres aux fonctions.
Exercice 1.8.2.
(suite de l'exercice
1.6.2 sur la suite de Syracuse).
- Ecrire une fonction qui prend un entier en entrée et renvoit si est pair ou sinon.
- Pour donné, on note la plus petite valeur de telle que . Faire une fonction qui prend un entier en entrée et renvoit .
- Afficher les valeurs de pour les valeurs de . Le résultat sera de la forme:
x= 1 T= 1
x= 2 T= 2
x= 3 T= 6
x= 4 T= 3
x= 5 T= 5
x= 6 T= 7
x= 7 T= 12
x= 8 T= 4
x= 9 T= 14
x= 10 T= 6
etc
Solution:
def S(x):
if(x%2==0):
return x/2
else:
return (3*x+1)/2
def T(x):
T0=1
while(x!=1):
x=S(x)
T0 = T0+1
return T0
for x in range(1,100):
print ('x=', x, 'T=',T(x))1.8.2 Récursivité
La récursivité est lorsqu'une fonction s'appelle elle même. Regarder l'exemple suivant et essayer de comprendre ce qu'elle fait.
Ecrire:
def f(n):
if(n>1):
return n*f(n-1);
else:
return 1;
print(f(5))
Résultat:
120
Chapitre 2 Objets plus élaborés
2.1 Vecteurs, matrices et algèbre linéaire
2.1.1 Vecteurs et représentation graphique
Voici comment utiliser arange() pour créer une liste de nombres. Comme pour 'list', les indices commencent à 0. Ecrire:
from pylab import *
from numpy import *
X=arange(0, 6, 0.5) # crée une liste de nombres X_{i} de 0 à 6 (exclu) par pas de 0.2 (il y a donc 6/0.2 = 30 éléments)
print ('X = ', X)
Y=sin(X) # crée une liste où chaque élément est Y_{i}=\sin\left(X_{i}\right)
print ('Y = ', Y)
plot(Y) # dessin des valeurs de \left(Y_{i}\right)_{i} en fonction de i
show() # montre le dessin
plot(X,Y) # dessin des valeurs de Yi en fonction des Xi
xlabel('x') # rajoute titre aux axes
ylabel('y=sin(x)')
show() # montre le dessin
résultat:
X = [ 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. 5.5]
Y = [ 0. 0.47942554 0.84147098 0.99749499 0.90929743 0.59847214
0.14112001 -0.35078323 -0.7568025 -0.97753012 -0.95892427 -0.70554033]

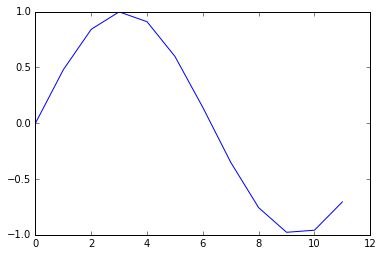
Pour connaitre le type des tableaux et listes de l'exemple précédent, écrire ensuite:
print (type(X))
résultat:
<class 'numpy.ndarray'>
Il y a une autre possibilité pour créer une liste de nombres avec linspace(). écrire:
from pylab import *
from numpy import *
X=linspace(0,1,10) # 10 nombres équidistribués de à compris
Y=sin(X)
plot(Y, marker='o', linestyle='solid') # options pour le dessin
show()
résultat:
Ecrire
from numpy import *
zeros(10) # liste de nombres tous égaux à zéro
Résultat:
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
Conversion list->array avec la fonction asarray:
Il peut être utile de convertir une liste de nombres de type 'list' en une liste de type 'numpy.ndarray' afin de la dessiner par exemple.
Ecrire:
from pylab import *
from numpy import *
Y = [0,1,4,9,16]
print (type(Y))
Y = asarray(Y)
print(type(Y))
plot(Y)
Résultat:
<class 'list'>
<class 'numpy.ndarray'>
Copie de tableaux:
On a vu que pour copier une liste L1 dans un nouvel objet L2 il faut écrire L2=list(L1) . De la même façon pour copier un tableau T1 dans un nouveau tableau T2 il faut écrire: T2 = np.copy(T1). Ecrire:
import numpy as np
T1 =arange(0, 2, 0.5) # crée une liste de nombres X_{i} de 0 à 2 (exclu) par pas de 0.5
T2 = copy(T1) # copie dans objet distinct
T3 = T1 # attention, ce n'est pas une vraie copie: T3 sera seulement un autre nom pour T1
T2[0] = 10
T3[0] = 20
print ('T1 = ', T1)
print ('T2 = ', T2)
print ('T3 = ', T3)
Résultat:
T1 = [ 20. 0.5 1. 1.5]
T2 = [ 10. 0.5 1. 1.5]
T3 = [ 20. 0.5 1. 1.5]
2.1.2 Matrices et représentation graphique
2.1.2.1
Premier exemple
from pylab import *
from numpy import *
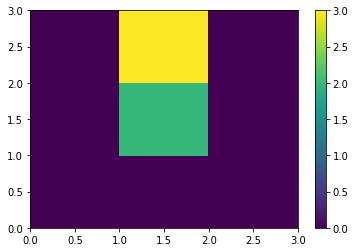
A=zeros([3,3]) # matrice remplit de zeros
A[1,1]=2 # on modifie un élément
A[2,1]=3
print (A)
pcolormesh(A) # dessin des contours des valeurs
colorbar() # rajoute une barre des valeurs
show()
résultat:
[[0. 0. 0.]
[0. 2. 0.]
[0. 3. 0.]]
2.1.2.2 Autres représentations graphiques
2.1.2.3 Création de matrices
Matrice avec valeurs aléatoires:
Ecrire
from pylab import *
from numpy import *
random.uniform(-1, 1, size=(3,3)) # matrice 3*3 avec éléments aléatoires dans
Résultat:
array([[ 0.40517391, -0.47365213, -0.5208182 ],
[-0.23394281, 0.0347132 , -0.92326085],
[-0.94118242, -0.58734857, -0.19587783]])
Matrice identité:
from pylab import *
from numpy import *
eye(3)
Résultat
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
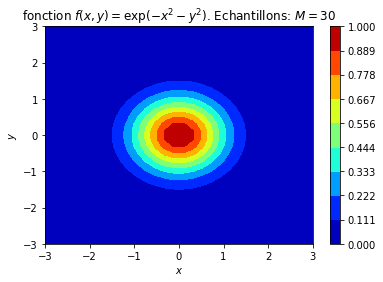
2.1.2.4 Matrice comme produit tensoriel de vecteurs
L'exemple suivant montre comment à partir de deux vecteurs et on peut construire une matrice . On termine l'exemple par une représentation graphique.
from pylab import *
from numpy import *
xmin,xmax,ymin,ymax = -3,3, -3,3 # bornes du domaine
M = 30 # nombre de points en x et y
x = linspace(xmin,xmax,M) # vecteur avec M nombres entre xmin et xmax
y = linspace(ymin,ymax,M)[:,newaxis] # vecteur dans la 2eme dimension
z = exp( -x*x-y*y) # matrice
levels = linspace(0,1,10) # defini les lignes de niveaux
contourf(z,levels,extent=(xmin,xmax,ymin,ymax))
colorbar()
xlabel('$x$')
ylabel('$y$')
title('fonction $f(x,y)= \exp (-x^2 -y^2)$. Echantillons: $M='+ ('%4i'%M)+'$')
Résultat:
2.1.3 Opérations d'algèbre linéaire
2.1.3.1 opérations élémentaires
Ecrire
import numpy as np
from scipy import linalg
A = np.array([[2,1],[1,1]]) #matrice
V = np.array([[1], [1]]) # vecteur colonne
print ('A=\n', A , '\nV=\n', V)
print ('A*V=\n', np.dot(A,V)) # produit matrice * vecteur
print ('A*A=\n', np.dot(A,A)) # produit matrice * matrice
d = linalg.det(A) #calcule le determinant
print ('det(A) = ', d)
Résultat:
A=
[[2 1]
[1 1]]
V=
[[1]
[1]]
A*V=
[[3]
[2]]
A*A=
[[5 3]
[3 2]]
det(A) = 1.0
2.1.3.2 Valeurs propres et vecteurs propres
On rappelle que si est une matrice diagonalisable alors sa diagonalisation donneoù est la matrice diagonale des valeurs propres et est une matrice contenant en colonnes les composantes des vecteurs propres (à droite) , qui vérifient
Ecrire:
from pylab import *
from numpy import *
M = array(([1,3,3],[1,4,3],[1,3,4])) # matrice
D, P = eig(M) # -> valeurs propres D et matrice des vecteurs propres P
R = dot( dot(P , diag(D)) , inv(P)) # R = P * D * P^(-1)
print ('M=\n' ,M, '\n P*D*P^(-1) =\n' , R)
Résultat:
M=
[[1 3 3]
[1 4 3]
[1 3 4]]
P*D*P^(-1) =
[[1. 3. 3.]
[1. 4. 3.]
[1. 3. 4.]]
Ecrire:
import pylab as py
import numpy as np
N = 100
A= 0.1
M = np.random.uniform(0, A, size=(N,N)) # matrice N*N avec éléments aléatoires dans [0,A]
EV = py.eigvals(M) # calcul des valeurs propres de M
# dessin des valeurs propres ------------------
plot(real(EV), imag(EV), linestyle = 'none', marker = 'o', c = 'lime',
markersize = 10)
a = 0.5*sqrt(N)*A
xmin,xmax,ymin,ymax = -a,a,-a,a
plt.axis([xmin,xmax,ymin,ymax]) # selectionne la vue
xlabel('$\Re(z)$')
ylabel('$\Im(z)$')
title('Eigenvalues of a random $' + ('%d'%N) +'*'+ ('%d'%N) +'$ matrix with iid elements in $[0,' + ('%4.2f'%A) +']$')
Résultat:
2.1.3.3 Matrices creuses (sparse)
Dans de nombreux problèmes on doit utiliser des matrices de taille très grande, (
ou plus) mais avec seulement un petit nombre d'éléments non nuls. Dans ce cas l'ordinateur stocke seulement la liste des éléments non nuls. Ce mode de stockage s'appelle «
matrice creuse ».
2.2 Objets graphiques avec Matplotlib
Programmes avec graphisme:
Afin de pouvoir interagir avec les fenetres graphiques, dans spyder il est conseillé, dans le menu Outils/Préférences/ConsoleIPython/Graphiques/Sortie : de choisir le mode automatique.
(et relancer la fenetre IPython)
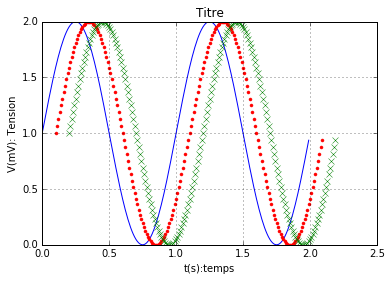
2.2.1 Courbe 1Dim simple
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
t = np.arange(0.0, 2.0, 0.01) # liste de nombre de 0 a 2 par pas de 0.01
s = 1 + np.sin(2 * np.pi * t)
plt.plot(t, s) # points relies (bleus)
plt.plot(t+0.1, s, 'r.') # red (r) et points isoles (.)
plt.plot(t+0.2, s, 'gx') # green (g) et croix (x)
plt.xlabel('t(s):temps')
plt.ylabel('V(mV): Tension')
plt.title('Titre')
plt.grid()
plt.savefig('V-t.png') # sauvegarde fichier image au format png
plt.show()
Résultat:
Documentations spécifiques:
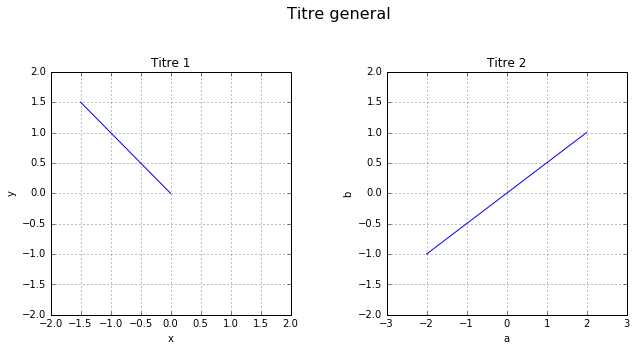
2.2.2 Des sous figures, titres et labels sur les axes
Ecrire:
import matplotlib.pyplot as plt
#-- preparation des figures
fig = plt.figure(1, figsize=(10, 5)) # taille X,Y en pouces (inchs)
plt.subplots_adjust(left=0.1, wspace=0.4, top= 0.8)
plt.suptitle('Titre general', fontsize=16)
#--- figure 1
xmin,xmax,ymin,ymax = -2,2,-2,2 # fenetre
f1 = plt.subplot(121) # Il y a 1*2 sous figures. f1 est la figure 1
plt.title('Titre 1')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
f1.plot([0,-1.5], [0,1.5]) # segment (0,0)->(-1.5,1.5)
f1.axis([xmin,xmax,ymin,ymax]) # selectionne la vue
#--figure 2
amin, amax, bmin, bmax = -3,3, -2, 2
f2 = plt.subplot(122) # Il y a 1*2 sous figures. f2 est la figure 2
plt.title('Titre 2')
plt.xlabel('a')
plt.ylabel('b')
plt.grid(True)
f2.plot([-2,2], [-1,1]) # segment (-2,-1)->(2,1)
f2.axis([amin,amax,bmin,bmax]) # selectionne la vue
plt.tight_layout() # pour que les differentes sous figures ne se superposent pas
Résultat:
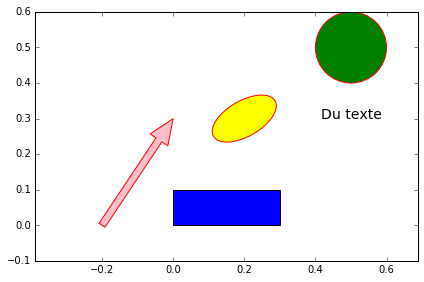
2.2.3 Des objets graphiques en dimension 2
Ecrire:
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.path as mpath
import matplotlib.lines as mlines
import matplotlib.patches as mpatches
from matplotlib.collections import PatchCollection
from math import *
fig, ax = plt.subplots()
#texte
x,y = 0.5, 0.3
plt.text(x, y, 'Du texte', ha="center", family='sans-serif', size=14)
# Un cercle
x,y = 0.5,0.5
r = 0.1
c = plt.Circle((x,y), r, facecolor= 'green', edgecolor= 'red')
ax.add_patch(c)
#Une ellipse
x,y = 0.2,0.3
rx,ry = 0.2, 0.1
angle = 30 # en degres
e = mpatches.Ellipse((x,y), rx, ry, angle, facecolor= 'yellow', edgecolor= 'red')
ax.add_patch(e)
# un rectangle
x,y = 0.,0. # coin inferieur gauche
dx,dy=0.3, 0.1 # taille
rec = plt.Rectangle((x,y), dx,dy, facecolor= 'blue', edgecolor= 'black')
ax.add_patch(rec)
#Une flèche
x,y = -0.2, 0. # départ
dx,dy=0.2, 0.3 # deplacement
width = 0.1
a = mpatches.Arrow(x, y, dx, dy, width, facecolor= 'pink', edgecolor= 'red')
ax.add_patch(a)
plt.axis('equal') # pour avoir meme echelle en x,y
#plt.axis('off') # n'affiche pas le cadre ni les axes
ax.autoscale_view() # pour que la figure s'ajuste aux objets
plt.show()
Résultat (selon les options):
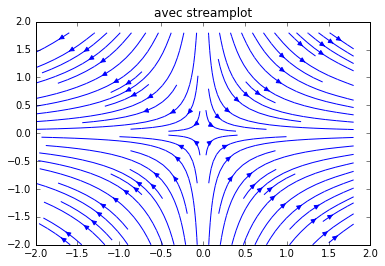
2.2.4 Dessin d'un champ de vecteur en dimension 2 avec streamplot() ou quiver()
Ecrire:
import numpy as np
import matplotlib.pyplot as plt
#fonction qui definit le champ de vecteur F
def F(x, y):
return x, -y
# reseau de points en x,y
xmin, xmax, dx = -2,2, 0.2
ymin, ymax, dy = -2,2, 0.2
X,Y = np.meshgrid( np.arange(xmin, xmax, dx), np.arange(ymin, ymax, dy) )
Fx, Fy = F(X,Y) # calcule le champ de vecteur sur le reseau
#----------------
plt.streamplot(X,Y, Fx,Fy)
plt.title('avec streamplot')
#----------------
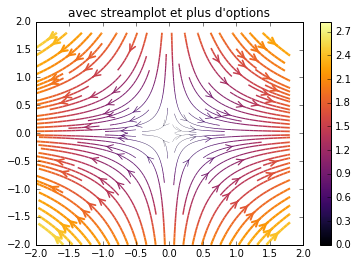
plt.figure() # nouvelle figure
norme = np.sqrt(Fx**2+Fy**2) # norme du champ F
strm = plt.streamplot(X, Y, Fx, Fy, color = norme, linewidth = norme, cmap=plt.cm.inferno, density=[1, 2], arrowstyle='->', arrowsize=1.5)
plt.colorbar(strm.lines) # montre l'echelle
plt.title("avec streamplot et plus d'options")
#----------------
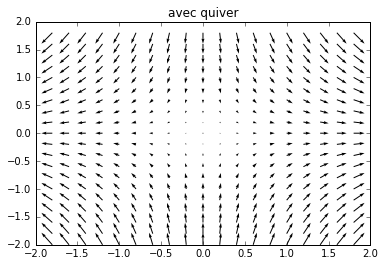
plt.figure() # nouvelle figure
plt.quiver(X,Y,Fx,Fy)
plt.title('avec quiver')
Résultat:
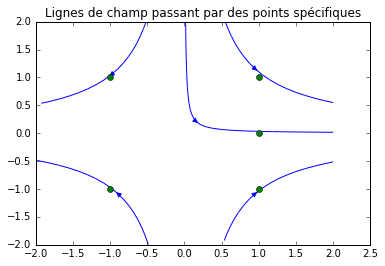
2.2.4.1 Dessin des lignes de champ passant par des points spécifiés avec streamplot()
Ecrire:
import numpy as np
import matplotlib.pyplot as plt
#definit le champ de vecteur F
def F(x, y):
return x, -y
# reseau de points en x,y
nx, ny = 64, 64 # nombre de points
x = np.linspace(-2, 2, nx) # 1dim array
y = np.linspace(-2, 2, ny)
X, Y = np.meshgrid(x, y) # 2dim array
Fx, Fy = F(X,Y) # calcule le champ de vecteur sur le reseau
# Liste de points (x,y)
points = np.array([[1, 1, -1, -1, 1], [0, 1, 1, -1, -1]])
plt.streamplot(x, y, Fx, Fy, start_points = points.T)
plt.plot(points[0], points[1], linestyle ='none', marker='o') # dessin des points
plt.title('Lignes de champ passant par des points spécifiques')
Résultat:
2.2.5 Créer une animation
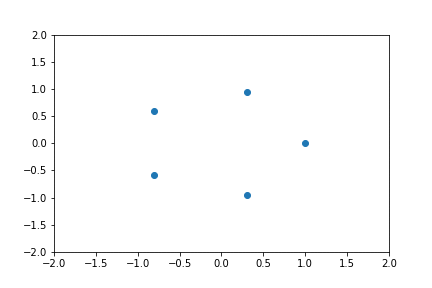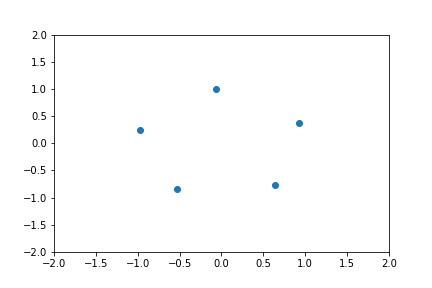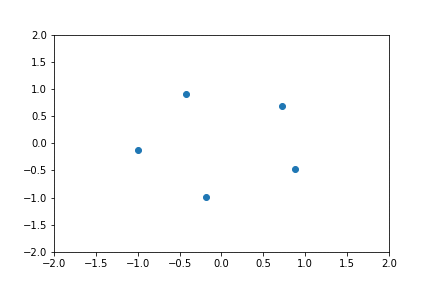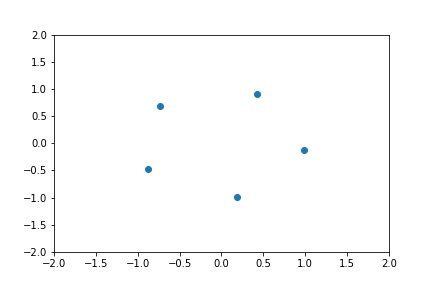
Dans l'exemple suivant on considère nombres complexes avec les indices et un déphasage fixé . Ces nombres sont équidistribués sur le cercle unité et on remarque que . Ainsi en faisant varier on verra les points tourner. Remarquer que et .
Ecrire:
import matplotlib.pyplot as plt
import numpy as np
import subprocess
from math import *
N, P = 5, 10 # nombre de points et nombre d'images,
xmin,xmax,ymin,ymax = -2,2,-2,2
for p in range(P): # boucle p = 0,1..,P-1
x = p/P
j = np.arange(N) # liste 0->(N-1)
X = np.cos(2*pi*(j+x) /N) # liste des X_j(x)
Y = np.sin(2*pi*(j+x) /N) # liste des Y_j(x)
plt.cla() # efface le graphisme precedent
plt.plot(X,Y, linestyle='none', marker='o')
plt.axis([xmin,xmax,ymin,ymax]) # selectionne la vue
plt.pause(0.01) # montre la figure et attend 0.01 sec.
plt.show() #laisse la figure à la fin et attend qu'on la referme
Pour voir le résultat, ouvrir un terminal (fenêtre de commandes) et lancer le programme par: python3 programme.py
Résultat:
2.2.6
Créer une animation et crée un fichier gif animé avec convert ou gifsicle
Voici le même programme que ci-dessus, mais avec deux instructions supplémentaires (
savefig() qui sauve chaque image dans la boucle et
convert... qui fabrique la vidéo finale), afin de fabriquer à la fin un fichier gif animé. Il faut avoir installé le logiciel
imagemagick.
import matplotlib.pyplot as plt
import numpy as np
import subprocess
from math import *
N, P = 5, 10 # nombre de points et nombre d'images,
xmin,xmax,ymin,ymax = -2,2,-2,2
for p in range(P): # boucle p = 0,1..,P-1
x = p/P
j = np.arange(N) # liste 0->(N-1)
X = np.cos(2*pi*(j+x) /N) # liste des X_j(x)
Y = np.sin(2*pi*(j+x) /N) # liste des Y_j(x)
plt.cla() # efface le dessin precedent
plt.plot(X,Y, linestyle='none', marker='o')
plt.axis([xmin,xmax,ymin,ymax]) # selectionne la vue
plt.savefig('image_' + str(p).zfill(4) + '.png', dpi=50) # sauve fichier image (pour ensuite gif anime). dpi: precision de l'image
plt.pause(0.0O1) # montre la figure et attend 0.001 sec.
#--- cree un fichier gif anime. delay en 1/100s.-----------------------------
subprocess.getoutput('convert -delay 10 -loop 0 image_*.png animation.gif') #fabrique fichier gif final
subprocess.getoutput('rm image_*.png') # efface les fichiers images temporaires
print ('fichiers animation.gif cree. Veuillez le lire avec firefox par exemple.')
Pour voir le résultat, ouvrir un terminal (fenêtre de commandes) et lancer le programme par: python3 programme.py
Résultat:
fichier animation.gif cree. Veuillez le lire avec firefox par exemple.
Pour visualiser le fichier produit, il faut l'ouvrir avec un navigateur (firefox par exemple). Ce fichier se trouve dans votre répertoire de travail.
2.2.6.1 Avec Gifsicle:
On peut aussi utiliser
gifsicle pour fabriquer le fichier gif animé final. L'utilisation de gifsicle est conseillée, car les fichiers sont plus compressés.
Il faut remplacer la ligne subprocess.getoutput('convert -delay 10 -loop 0 image_*.png animation.gif')
par:
subprocess.getoutput('convert image_*.png GIF:- | gifsicle --delay=10 --loop --optimize=2 --colors=256 --multifile - > animation.gif')
2.2.7 Capturer les évènements de la souris (clic, position) et du clavier
Avec le programme on crée un point rouge en cliquant sur la fenetre. On déplace le point rouge avec les 4 flèches du clavier.
Ecrire:
import numpy as np
import matplotlib.pyplot as plt
x, y = 0,0 # point
#---- si evenement souris (clik)
def on_click(event):
global x,y
x, y = event.xdata, event.ydata # coord souris en x,y
print('click en x=',x,' y=',y)
plt.plot(x,y, 'r.')
plt.pause(0.001) # montre le dessin sans bloquer
#---- si evenement clavier
def on_key(event):
print('key = ', event.key)
global x,y
# print('you pressed', event.key, event.xdata, event.ydata)
if event.key == 'right':
x=x+1
elif event.key == 'left':
x=x-1
elif event.key == 'up':
y=y+1
elif event.key == 'down':
y=y-1
plt.plot(x,y, 'r.')
plt.pause(0.001) # montre le dessin sans bloquer
#----------------------------
plt.axis([-10,10,-10,10]) # selectionne la vue
#plt.axis('equal') # pour avoir meme echelle en x,y
plt.connect('button_press_event', on_click) # associe la fonction aux evenements souris
plt.connect('key_press_event', on_key) # associe la fonction aux evenements clavier
plt.show() # bloque le programme ici pour gérer les evenements2.3 (Supplément) Dictionnaires (dict)
Un dictionnaire est également un type de liste d'objet, mais au lieu de repérer les objets par un indice commençant à 0, les différents objets sont accessible à l'aide d'une clef, qui peut être un objet quelconque.
Ecrire:
fra_deu={'un':'ein','trois':'drei','deux':'zwei'} # Création
fra_deu['trois'] # Accès à un élément du dictionnaire
résultat:
'drei'
Ecrire:
fra_deu['quatre'] # Clef n'existant pas !
résultat:
Traceback (most recent call last):
File '<stdin>', line 1, in ?
KeyError: 'quatre'
Ecrire:
fra_deu['quatre']='vier' # Ajout de l'entrée manquante
fra_deu['quatre']
résultat:
'vier'
Vous pouvez obtenir les différentes fonctions disponibles pour un dictionnaire avec la commande help(dict).
Chapitre 3 Lecture et écriture de fichiers
On crée un objet fichier Python avec la fonction open() :
MonFichier = open('NomDuFichier','r')
Le mode peut être 'r' (read, en lecture seule), 'w' (en écriture seule), 'a' pour rajouter à la fin du fichier, D'autres modes (mixte lexture/écriture, etc) existent. La lecture des fichiers texte (i.e. non binaires) se fait avec les fonctions read(), readline() et readlines():
MonFichier.read() # Lit la totalité du fichier sous forme d'un chaîne de caractères
MonFichier.readline() # Lit la ligne suivante du fichier, sous forme d'une chaîne de caractères
MonFichier.readlines() # Lit toutes les lignes du fichier sous forme d'une liste de chaînes de caractères
Monfichier.write('toto') # écrit
Pour lire une liste de nombres contenu dans une ligne, il suffit de lire cette ligne avec la fonction readline(), puis de séparer les nombres avec la fonction split(). Par exemple :
f=open('tmp0','r')
ligne=f.readline() # lecture d'une ligne
print (ligne) # Ecriture de la ligne sous forme d'une chaîne de caractères
print ligne.split() # On sépare les éléments -> liste
print float(ligne.split()[1]) # Conversion en nombre réel 0.2
f.close() # referme le fichier
résultat:
Toto 1.8 9.2
['Toto', '0.2', '9.2']
help(file) permet de lister l'aide sur l'utilisation des fichiers.
Ecriture/Lecture de données formatées:
On utilise le module pickle. Cela permet d'écrire des données et lire des données en conservant leur type (nombre, liste, chaine de caractère etc).
Pour écrire:
import pickle
x=2
f=open('fichier','w')
pickle.dump(x,f)#écrit x
f.close()
Pour relire:
f=open('fichier','r')
x=pickle.load(f)#lit x
f.close()
print x
résultat:
2
Chapitre 4
Résoudre une équation différentielle ordinaire (EDO) avec Scipy
4.1 Généralités sur les équations différentielles ordinaires (EDO)
Une équation différentielle ordinaire (EDO) est une équation de la formeoù l'inconnue est la fonction à composantes:alors que la fonction et la condition initiale sont supposées connues.
4.1.1 Transformer une équation différentielle d'ordre en EDO
Prenons un exemple. L'équation du deuxième ordre en temps:peut se ré-écrire comme une équation du premier ordre à deux variables en posant et , et .
Plus généralement une équation différentielle d'ordre à variable :peut se réécrire comme une équation d'ordre 1 avec variables . Il suffit de poser , , , , c'est à dire , , , . Ainsi l'équation se ré-écrit:avec
4.2 Résoudre numériquement une EDO avec le langage python
On va utiliser une fonction appelée odeint(). Le principe est de donner les conditions initiales , d'écrire la fonction , et de donner un tableau de valeurs du temps . En retour la fonction odeint() renvoit un tableau de valeurs tel que est la solution de l'ODE avec les conditions initiales spécifiées.
On peut passer des paramètres extérieurs à la fonction.
4.2.1 Exemple 1
On considère l'équation différentielle ordinaire à composante suivante où l'inconnue est la fonction :
Ecrire:
%matplotlib inline
from scipy.integrate import odeint
from pylab import *
from numpy import *
y_in = 0.1 # condition initiale
tmax= 50 # intervalle de temps
N = 501 # nombre de points en temps
def f(y,t):
return y*sin(t)
t = linspace(0, tmax, N) # tableau de t = 0->tmax avec N valeurs
y = odeint(f, y_in,t)
plot(t,y)
xlabel('$t$')
ylabel('$y(t)$')
title("Solution de $y'(t)=y sin(t)$")
Résultat:
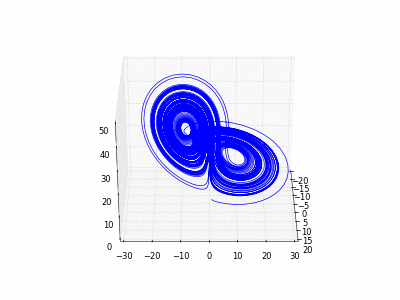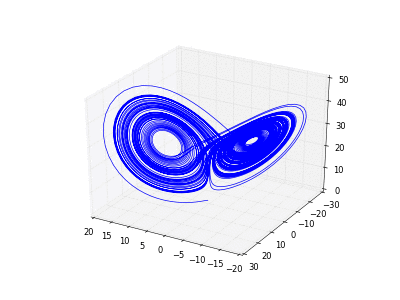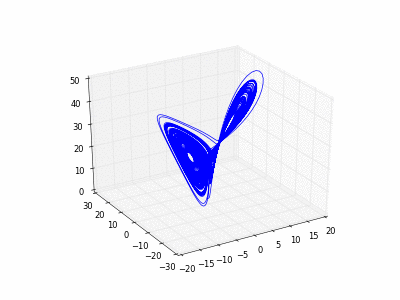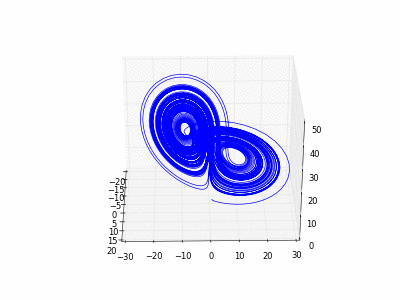
4.2.2
Exemple 2
(
4.2.2).On considère l'équation différentielle ordinaire à
composantes suivante appelées
équations de Lorenz. L'inconnue est la fonction
:
On connait les conditions initiales et les paramètres .
Ecrire:
#%matplotlib inline
from numpy import *
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
sigma, beta, rho = 10, 8/3., 28 # parametres
y_in = [0, 1, 1.05] # Conditions initiales
tmax= 100 # intervalle de temps
N = 10000 # nombre de points en temps
def f(y,t,sigma, beta, rho):
"""The Lorenz equations."""
f0 = -sigma*(y[0] - y[1])
f1 = rho*y[0] - y[1] - y[0]*y[2]
f2 = -beta*y[2] + y[0]*y[1]
return f0,f1,f2
t = linspace(0, tmax, N) # tableau de t = 0->tmax avec N valeurs
y = odeint(f, y_in, t, args=(sigma, beta, rho))
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(y.T[0], y.T[1], y.T[2])
#plt.show()
# rotate the axes and update
for angle in range(0, 360):
ax.view_init(30, angle)
plt.draw()
plt.pause(.001) # montre image
Résultat: (on a fabriqué ce fichier gif animé d'après la Section
2.2.6 avec gifsicle)
Chapitre 5 Micro-projets
Dans ce chapitre, nous vous proposons de réaliser des micro-projets. Ce sont des programmes rapides à réaliser (quelques lignes de code), afin de vous montrer l'aspect ludique et créatif de la programmation, et aussi pour résumer différentes notions vues dans les chapitres précédents.
Nous demandons de produire un
compte rendu sous forme pdf et html, que l'on rédigera avec
Lyx (qui permet de créer des documents scientifiques) et exportée en html (avec LyxHtml) et en pdf: pour apprendre Lyx, voici un
document en pdf qui sert d'exemple et d'exercice. Voici le même
document en html, qui vous servira éventuellement pour copier/coller. Dans ce compte rendu qui sert d'exercice, il devra y avoir au moins une équation en ligne, une équation dans le texte, une figure, et une table des matières.
La Section suivante donne quelques recommandations générales et prélables pour effectuer un projet de programmation.
5.1 Introduction aux micro-projets
5.1.1 Que faire avant de programmer?
Avant de se retrouver devant un ordinateur pour écrire un programme, il faut avoir établi clairement ce qu'on désire lui faire faire. Voici l'ensemble des étapes à suivre, indispensables, à faire au préalable devant une feuille de papier.
- Définir clairement l'objectif du programme (surtout s'il y a plusieurs personnes à y collaborer).
- Définir l'ensemble des tâches qui doivent être accomplies dans un ordre logique pour atteindre cet objectif. Pour un projet scientifique il faut que toutes les formules mathématiques soient bien écrites.
- Tracer sur un papier un organigramme illustrant le fonctionnement de votre programme. Vérifiez que l'ordre d'exécution des diverses tâches va effectivement faire ce que vous attendez.
En fait, votre organigramme se traduira directement dans la partie principale de votre programme (fonction int main()). A chaque tâche correspondra l'appel d'une sous partie (une fonction).
- Déterminez la méthode (algorithme) permettant de remplir chaque tâche. Il est possible qu'une sous-tâche soit commune à plusieurs fonctions. Dans ce cas, faites-en une nouvelle fonction. Cependant, pour éviter une multiplication de ces fonctions, ne le faites que pour celles faisant plusieurs lignes de programme. L'art de la programmation consiste à trouver un compromis entre la simplicité, la longueur, et la rapidité d'éxécution de votre programme.
- Si le programme effectue des taches complexes et “imprévisibles”, imaginer des situations simples où l'on connait la solution et qui permettront de tester le programme.
5.1.2 Quelques notions de qualité en informatique
La qualité d'un programme ne se traduit pas simplement en termes d'efficacité mais également en termes de sécurité (fiabilité) et d'exportabilité. Autrement dit, vous devez écrire votre programme de telle sorte (1) que n'importe qui puisse le lire et comprendre ce qu'il fait et (2) qu'il puisse être aisément testé. Voici quelques indications:
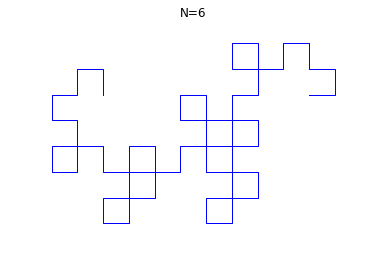
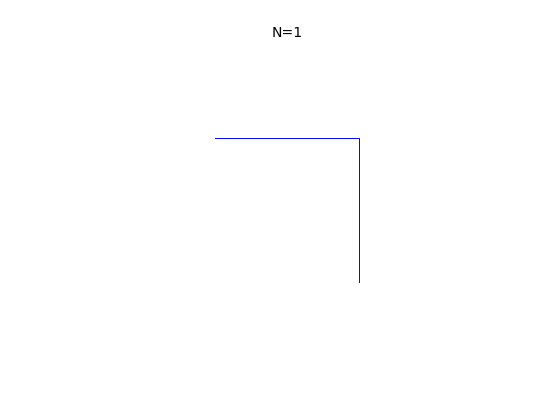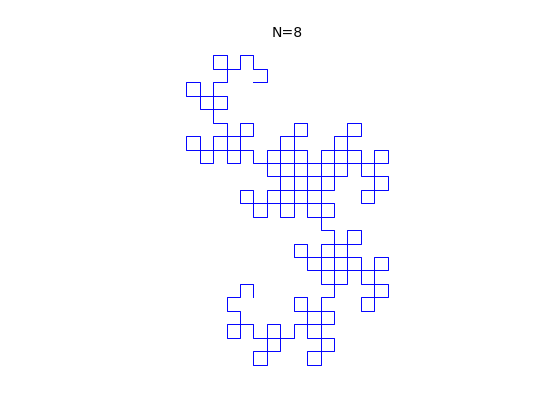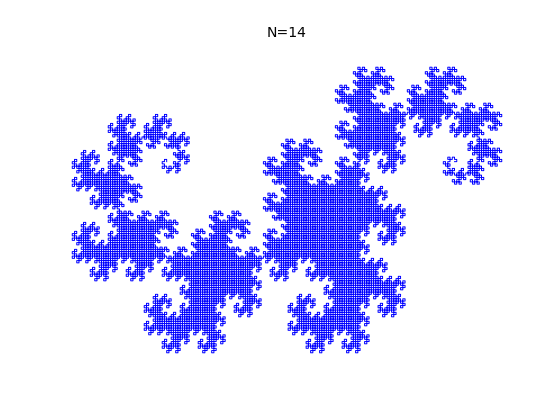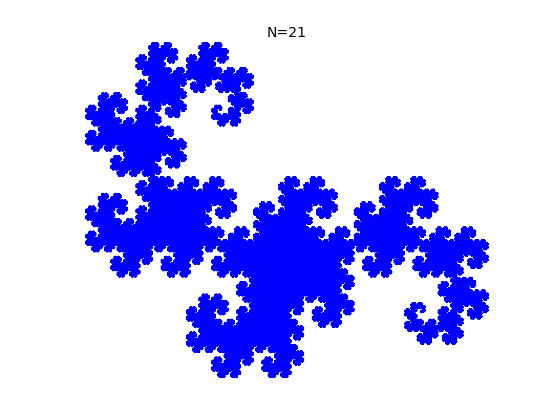
5.2 La fractale du dragon
Difficulté: moyenne.
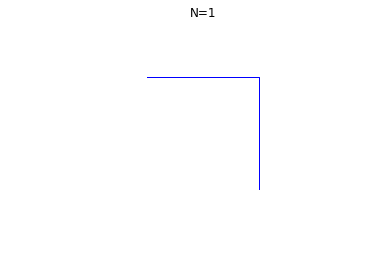
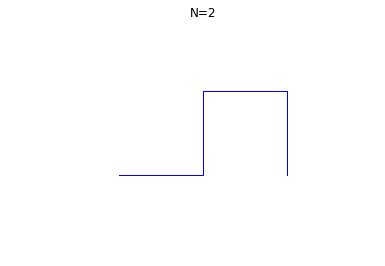
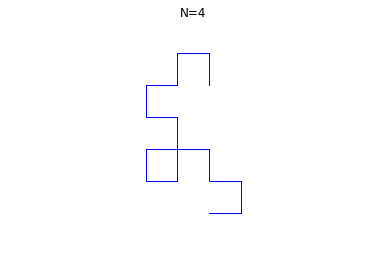
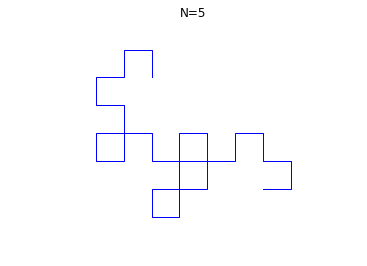
Si on prend un ruban de papier, et que l'on replie le coté gauche sur le côté droit, puis ainsi fois en rabattant chaque fois la gauche sur la droite, que l'on déplie le ruban et impose à chaque pli de faire un angle droit (90°) on obtient les formes suivantes assez surprenantes, ici pour :
L'objectif de ce micro-projet est de dessiner ces figures pour
quelconque, de façon automatique et d'observer l'apparition de la
fractale du dragon. Voir aussi
suite de pliage.
Exercice 5.2.1.
(Mathématiques) On peut coder la forme à fixé, comme une suite de valeurs , où signifie que le pli est dans le sens direct, et dans le sens indirect. D'après les images ci-dessus, , , . Montrer que la suite se déduit facilement de la suite par une formule simple.
Solution 5.2.2.
On aoù est la suite écrite à l'envers avec l'opposé des éléments.
Exercice 5.2.3.
« Dragon, étape 1 ».(Programmation sans graphisme) Ecrire un algorithme sur papier puis un programme qui construit la suite . Afficher la liste pour vérifier. Aide: on peut utiliser le type 'list' et chercher (sur internet ou dans le cours) comment copier une liste, inverser une liste et concaténer des listes.
Exercice 5.2.5.
« Dragon, étape 2 »(Programmation avec graphisme) Ensuite, pour la partie graphique, écrire un algoritme sur papier puis un programme qui dessine la fractale du dragon. Il suffit de lire la liste et dessiner des segments à la suite.
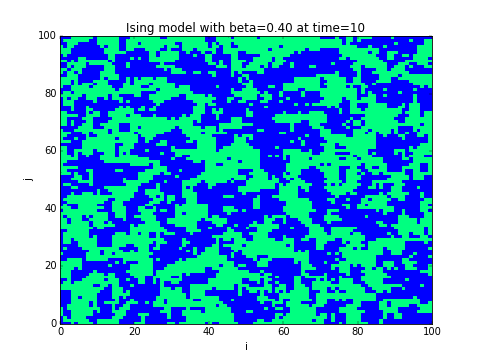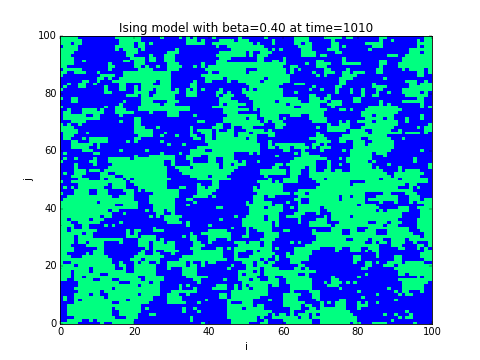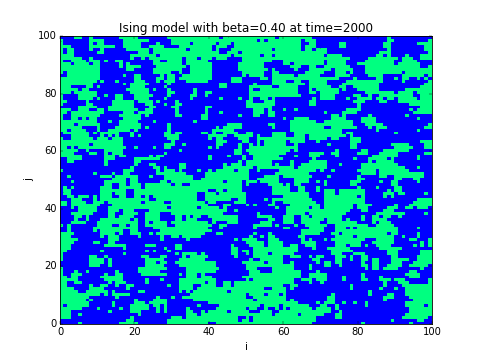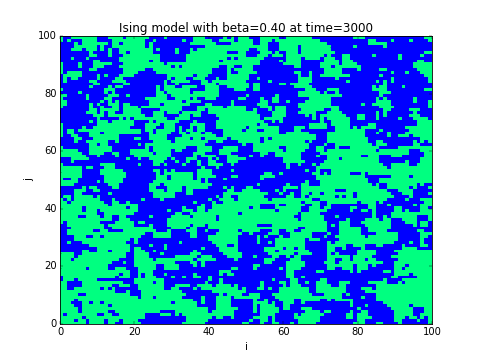
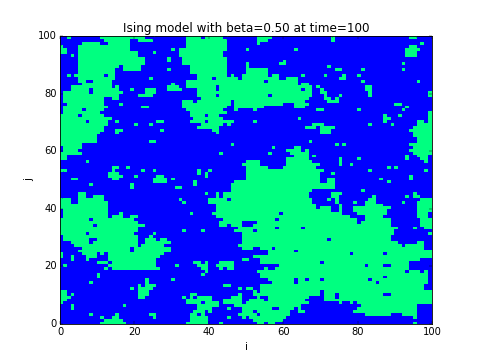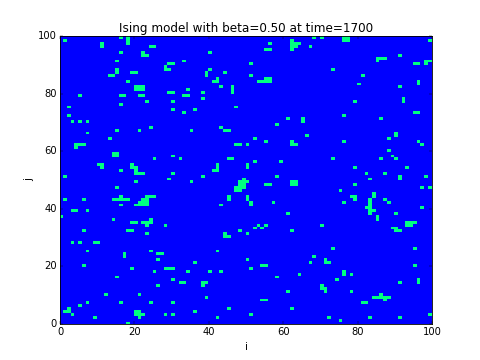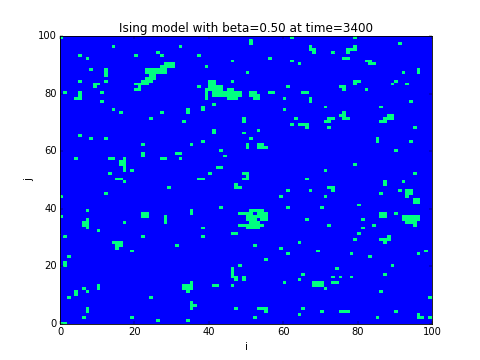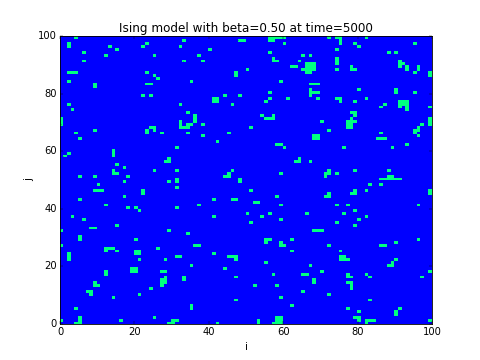
5.3 Algorithme de Monte-Carlo pour le modèle d'Ising
Difficulté: moyenne à difficile.
On considère un réseau périodique dont les sites sont notés et dont les variables sont et modélisent des spins (up/down). Si deux sites sont voisins (chaque site a 4 voisins) on note . Une configuration des spins est un champ donné: . Son énergie ferromagnétique est:
5.3.1 Algorithme de Monte-Carlo
L'algorithme d'évolution suivant est appelé
algorithme de montecarlo
.
est un paramètre fixé qui est l'inverse de la température:
.
- A l'instant , on part d'une configuration choisie au hasard.
- On choisit un site au hasard, et on note la configuration identique à sauf au site où le spin est opposé: (spin opposé).
- Choix de la configuration à l'instant :
- Si on choisit la configuration .
- Si on choisit la configuration avec la probabilité (et on choisit avec la probabilité complémentaire).
- On revient en (2) pour poursuivre l'évolution du champ de spins.
Exercice 5.3.3.
- Montrer que la condition s'écrit simplement en fonction du site et de ses voisins.
- Ecrire un programme qui partant d'un champ se spins initial aléatoire , le fait évoluer selon l'algorithme de Monte-Carlo et le représente après chaque itérations.
- L'aimantation de la configuration est . Représenter l'aimantation au cours du temps. Quand l'équilibre statistique est atteind, calculer la moyenne et la variance . Représenter et en fonction de .
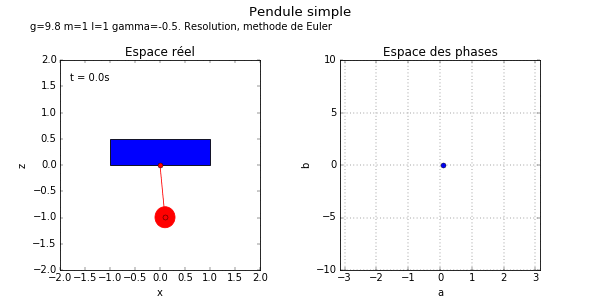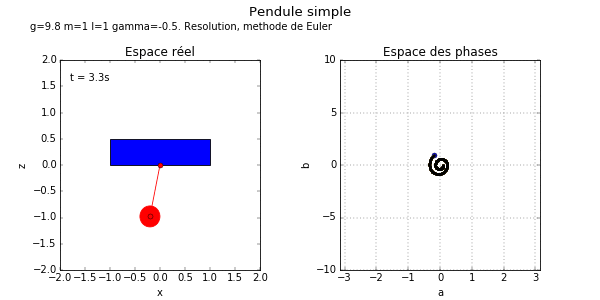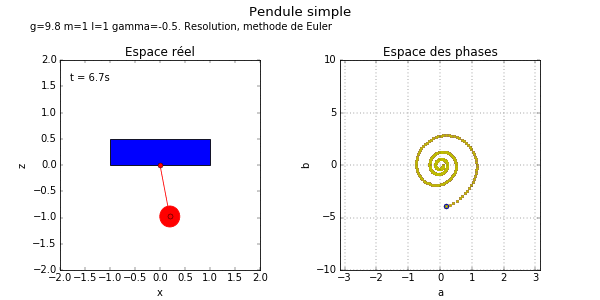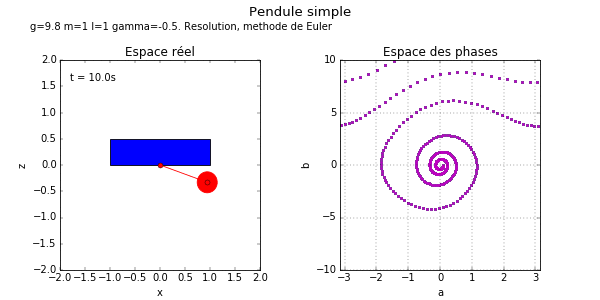
5.4 Le pendule (système dynamique, ODE)
L'objectif est de dessiner (créer une animation) dans l'espace réel et dans l'espace des phases, le mouvement d'oscillation d'un
pendule simple de masse
, longeur
, fixées, soumis à la force de pesanteur
avec
et à une force de frottement de coefficient
.
5.4.1 Equations physiques
si
est la position angulaire et
la vitesse angulaire au temps
on a
où
sont des fonctions de
. L'espace des phases est la plan
.
La position du pendule dans le plan vertical est:
Exercice 5.4.1.
(Mathématiques sur le papier).
- Vérifier les formules (1) en appliquant la loi de Newton sur la droite verte tangente au cercle.
- Pour les petites oscillations, sans frottement, c'est à dire , et , linéariser les équations du mouvement et montrer que la trajectoire du point est une ellipse parcourue dans le sens indirect avec une période
Solutions:
- Sur l'axe tangent au cercle, la loi de Newton s'écrit:
- Pour , les équations linéarisées sont donc
On pose
alors
dont la solution est
(mouvement circulaire indirect) avec la période
.
5.4.2 Méthode de résolution numérique de Euler
On a . Si , alors au premier ordre on peut écrire, d'après la formule de Taylor:et de même pour .
La
méthode de Euler, consiste à considèrer un petit intervalle de temps
et de négliger le terme
. Ainsi on écrit:
Voici comment on utilise ces formules. On choisit un pas de temps très petit. Par exemple On discrétise le temps avec un pas de temps : la date de départ est . ensuite il y a , , etc..
On suppose que sont les conditions initiales connues. Avec les formules de Euler on calcule , puis , etc
5.4.3 Programmation
A chaque étape suggérée ci-dessous, tester votre programme.
Exercice 5.4.2.
« Etape 1, sans graphisme ».
- Déclarer les paramètres suivants comme variables globales: le pas de temps , conditions initiales . Calculer et afficher . Tester ce programme.
- Définir une fonction qui en entrée prend et renvoit d'après les lois du mouvement (1). Tester cette fonction avec quelques valeurs.
- Faire une boucle sur par pas de temps et itèrer les formules de Euler (4). Afficher les valeurs de à chaque instant. Vérifier à la lecture des résultats que le point a bien parcouru un tour dans le sens indirect.
Exercice 5.4.4.
« Etape 2, avec graphisme ». Le but est d'obtenir les animations ci-dessous. Modifier et compléter le programme précédent pour
- Dans la boucle précédente de la méthode de Euler, rajouter quelques lignes de code qui font le dessin du pendule dans le plan vertical . Pour cela on utilisera la fonction plot() pour tracer un segment qui modélise la barre du pendule. Remarque: on fait le dessin du pendule à l'instant « présent » dans la boucle, il n'est donc pas utile d'utiliser une liste pour mémoriser les états passés.
- Rajouter le dessin du pendule dans l'espace des phases au cours du temps.
- Sauvegarder sous forme movie.mp4 et movie.gif (gif animé).
- Essayer avec et . Quel phénomène lié à l'approximation de Euler observez vous?
5.4.4 Méthode de résolution numérique avec la fonction odeint()
Afin d'avoir une meilleur précision (et rapidité) numérique on va remplacer l'approximation de Euler précédente par une approximation appelée « Runge Kutta » et qui est déjà implémentée dans la fonction odeint() expliquée en Section
4.
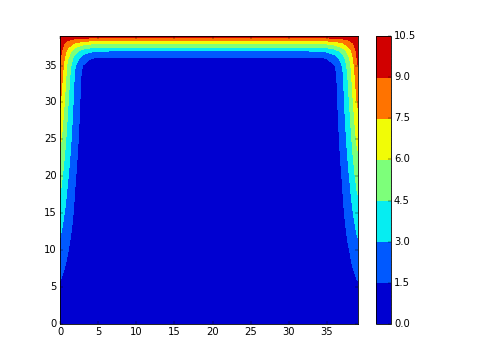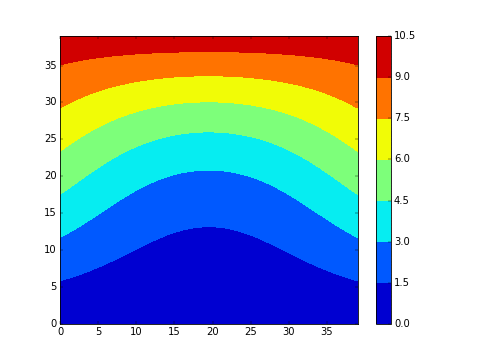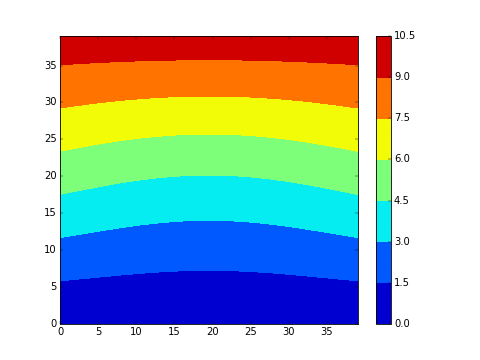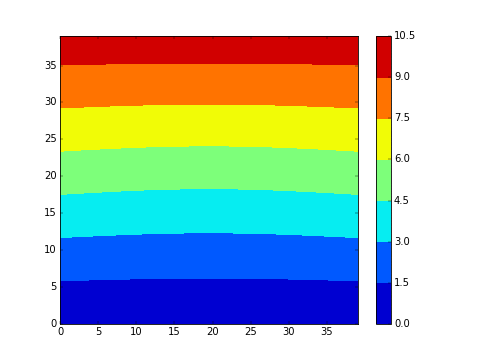
5.5 Equation de la chaleur
Difficulté: moyenne.
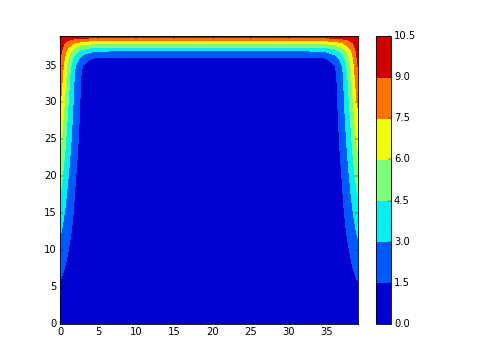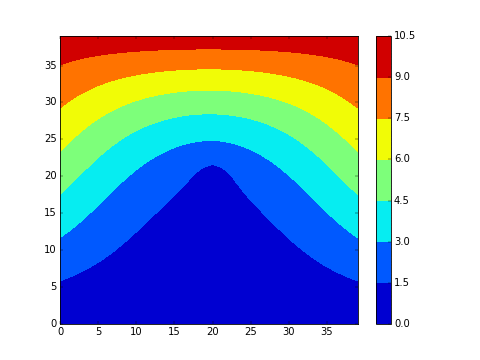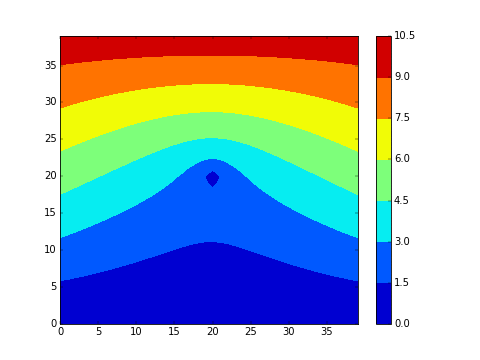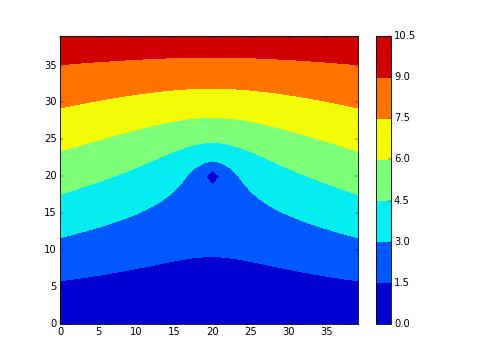
On souhaite visualiser la progression du champ de température dans un matériau lorsque la température est imposée et fixée au bords. Dans le premier exemple ci-dessous en dimension 2, la température initiale est 0 (bleu) partout et on impose un gradient de température au bord (chaud (rouge) en haut). Dans le deuxieme exemple, on impose de plus un point froid (à 0) au centre du matériau:
Notons
les variables d'espace et
la variable de temps.
Joseph Fourier a découvert en 1822 que la propagation de la température
dans un matériau est régit par l'équation d'évolution
appelée
équation de la chaleur, avec l'opérateur Laplacien:
La valeur de la température est imposée sur les bords du domaine.
On va modéliser cette évolution en dimension sur le domaine carré . On discrétise l'espace avec un pas très petit. On note donc , avec . Le champ de températures à l'instant est modélisé par une matrice de taille . On discrétise le temps avec un pas très petit et on note le champ de température à l'instant .
Exercice 5.5.1.
(Mathématiques) On remplaçant les dérivées par des différences finies montrer que l'équation de la chaleur ci-dessus devient (au premier ordre en ):
avec
. Sur les 4 bords, c'est à dire en
on souhaite imposer un gradient de « température »
avec
fixé. Ecrire ce que cela impose pour la matrice
. Montrer que le processus est convergent si
. Quelle est la solution attendue de l'équation stationnaire
?.
Solution:
D'après la formule de Taylor au 1er ordre:
donc
De même
et de même pour
. On déduit
On a de même
Donc l'équation de la chaleur
donne
ce qui donne (
5).
Conditions aux bords . On a et avec . Sur les bords et cette condition s'écritSur le bord cette condition s'écrit Sur le bord cette condition s'écritLe processus est convergent si .
Exercice 5.5.2.
(Programmation)
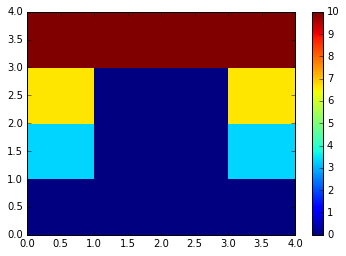
- Ecrire un programme qui définit (pour tester), , et initialise la matrice avec les valeurs aux bords et 0 à l'intérieur. Afficher la matrice et dessiner pour vérifier (Aide: Section 2.1.2.1). Le résultat devrait ressembler à:
N= 4
T=
[[ 0. 0. 0. 0. ]
[ 3.33333333 0. 0. 3.33333333]
[ 6.66666667 0. 0. 6.66666667]
[ 10. 10. 10. 10. ]]
- Écrire une fonction def Evolue(): qui fait évoluer tous les éléments du tableau T sur un pas de temps, d'après (5). Vérifier dans le cas et dessiner le tableau. Incorporer l'appel de cette fonction dans une boucle temporelle qui ne s'arrête que si le tableau n'évolue plus à près. Pour évaluer cela il faut mesure la norme (que l'on calcule au fur et à mesure dans la boucle sur ) et que la fonction Evolue() renvoie cette norme. Vérifier que vous obtenez la solution stationnaire attendue. Le résultat devrait ressembler à cela:
T=
[[ 0. 0. 0. 0. ]
[ 3.33333333 3.32288355 3.32288355 3.33333333]
[ 6.66666667 6.65621662 6.65621662 6.66666667]
[ 10. 10. 10. 10. ]]
norme= 9.67313700277e-05
- Modifier votre programme pour voir une animation. Avec , cela devrait ressembler aux animations présentées au début. Essayer différentes géométries.
5.6 Zeros d'un polynome aléatoire
On considère un polynome de degré et à coefficients aléatoires et indépendants, selon une loi uniforme :
On sait que
a
zéros
dans le plan complexe. Dessiner les
zéros du polynome et observez. Quelle conjecture avez vous? Consulter cet
article de Terence Tao et al.. On peut aussi considérer des coefficients complexes aléatoires:
avec
aléatoires et indépendants.
Aide: les zéros du polynome sont les valeurs propres de la “
matrice compagnon” du polynome. Construire cette matrice et utiliser une fonction pour trouver les valeurs propres.
Partie II
Compléments du langage python
Chapitre 6 Classes et Objets
Programmer une classe consiste à définir un nouveau type d'objets avec des opérations précises que l'on pourra faire avec. Vous avez utilisé par exemple la classe des nombres complexes déjà existante (écrite par d'autres informaticiens avant vous). Avec cette classe, on peut déclarer des variables complexes et effectuer directement des opérations sur les nombres complexes comme z3 = z1*z2*exp(z4),...sans devoir décomposer l'opération sur les parties réelles et imaginaires.
6.1 Exemple
Construisons par exemple une classe d'objets appelée Vecteur, et décrivant un déplacement dans le plan .
import math
import matplotlib.pyplot as plt
class Vecteur: # Déclaration de la classe
x,y = 4,3 # des variables membre de la classe, pour stocker les coordonnées
def Affiche(self): # fonction membre qui affiche les coordonnées
print ('x=', self.x, 'y=', self.y)
def Dessin(self): # fonction membre qui dessine le vecteur
plt.plot([0, self.x], [0, self.y], marker='o')
plt.show()
def Longueur(self): # fonction membre qui renvoie la longueur
self.L = math.sqrt(self.x**2 + self.y**2) # rajout d'une variable membre
return self.L
v = Vecteur() # Création d'un objet de type Vecteur
v.Affiche() # affiche ses coordonnées
v.Dessin() # dessin du vecteur
print ('L=', v.Longueur()) # affiche sa longueur
v.x = 0 # modification de x
v.Affiche() # affiche ses coordonnées
print ('L=', v.Longueur())
résultat:
x=4 y=3
L=5.0
x=0 y=3
L=3.0
6.1.1 Fonctions membres spéciales
Certaines fonctions membre ont des noms prédéfinis qui commence et finit par deux traits soulignés. Ces fonctions sont appelées dans des situations spécifiques.
6.1.1.1 Constructeur __init__
Cette fonction appelée « constructeur » est appelée à l'initialisation d'un nouvel objet. Ecrire:
import math
class Vecteur:
def __init__(self, x0, y0): # fonction constructeur
self.x, self.y = x0, y0
def Affiche(self): # fonction membre qui affiche les coordonnées
print ('x=', self.x, 'y=', self.y)
w = Vecteur(4, 3) # Création d'un objet avec le constructeur
w.Affiche() # affiche ses coordonnées
résultat:
x=4 y=3
6.1.1.2 Destructeur __del__
Le destructeur est la fonction qui est appelée lors de la destruction de l'objet. Il ne prend qu'un argument (self). Il peut servir à 'nettoyer' des données créées par l'objet.
6.1.1.3 Opérateurs __add__, __sub__, __mul__, __div__, __pow__
Au moment de leur utilisation ces fonctions sont appelées par les symboles respectivement (+, -, *, /, **). Ces fonctions prennent deux arguments, le premier qui est 'self' et un deuxième désignant le second membre de l'opération. Voici un exemple avec la fonction __add__()
import math
class Vecteur:
def __init__(self, x0, y0): # fonction constructeur
self.x, self.y = x0, y0
def Affiche(self): # fonction membre qui affiche les coordonnées
print ('x=', self.x, 'y=', self.y)
def __add__(self, w): # addition de deux vecteurs
return Vecteur( self.x + w.x, self.y + w.y)
v1 = Vecteur(1,2)
v2 = Vecteur(3,4)
v3 = v1 + v2 # cela appelle la fonction __add__(v1,v2)
v3.Affiche()
résultat
x=4, y=6
6.1.2 Héritage de classes
L'héritage permet de créer des classes qui héritent des propriétés de la (les) classe(s) parente(s).On peut ajouter des propriétés spécifiques à la classe « enfant ». L'héritage peut être très utile lorsque l'on génère de multiples classes ayant des propriétés similaires. Cela peut être aussi utile pour ré-utiliser du code, provenant par exemple d'une librairie développée par quelqu'un d'autre, en ajoutant quelques fonctions à une classe pré-existante.
Voici un exemple où la classe Segment hérite de Vecteur et rajoute l'information du point de départ.
import math
import matplotlib.pyplot as plt
class Vecteur: # Déclaration de la classe
def __init__(self, x0, y0): # fonction constructeur
self.x, self.y = x0, y0
def Dessin(self): # fonction membre qui dessine le vecteur
plt.plot([0, self.x], [0, self.y], marker='o')
plt.show()
class Segment(Vecteur): # Hérite de la classe Vecteur
def __init__(self, xO, yO, x1, y1, col0):
self.xO, self.yO = xO,yO # origine
self.x, self.y = x1, y1 # deplacement
self.col = col0 #couleur
def Dessin(self): # fonction membre qui dessine le segment
plt.plot([self.xO, (self.xO + self.x)], [self.yO, (self.yO + self.y)], self.col, marker='o')
plt.show()
s1 = Segment(0,0, 2, 1, 'blue')
s1.Dessin()
s2 = Segment(2, 1, 2, -1 ,'red')
s2.Dessin()
résultat:
6.1.3 Copie d'objets
Ecrire:
import copy
a = Vecteur(2, 1)
b = a # copie de l'adresse
c = copy.deepcopy(a) # copie de l'objet
a.x = 3
print('a.x=', a.x , ' b.x=', b.x, 'c.x=', c.x)
print( a==b, a==c)
résultat:
a.x= 3 b.x= 3 c.x= 2
True False
Chapitre 7 Analyse de données avec numpy
7.1 Curve fit
Chapitre 8 Quelques modules utiles
8.1 Commandes du systèmes d'exploitation
8.1.1 Exemple
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Programme python pour creation/destruction de repertoires.
"""
Instructions
===========
- sauvegarder ce programme dans un repertoire, par exemple dans /home/nadia/python
-Ouvrir un terminal.
- Se placer dans le repertoire voulu, où tu veux créer/détruire des répertoires, appelé "repertoire courant", par la commande:
cd repertoire
- Lancer le programme avec des informations supplementaires par exemple:
python3 /home/nadia/python/creation_repertoires.py NOM 2 5
- Sortie:
il cree les repertoires NOM_0002 NOM_0003 ... NOM_0005
dans le repertoire courant.
- option pour detruire ces repertoires (si ils existent) rajouter l'option "destroy" a la fin par exemple:
python3 /home/nadia/python/creation_repertoires.py NOM 2 5 destroy
Attention: il detruira les repertoires NOM_0002 ... NOM_0005, meme si ils contiennent des donnees.
Remarques:
- on peut modifier ces programmes pour changer des options, par exemple le nombre de zeros, etc..
References:
----------
sur le module os:
https://docs.python.org/fr/3.6/library/os.html
sur le formattage des entiers:
https://pyformat.info/
Informations utiles sur les commandes dans un terminal:
https://doc.ubuntu-fr.org/tutoriel/console_commandes_de_base
"""
#--- importation des librairies que l'on utilise
import os
import sys
#--- en entree sys.argv est une liste avec les parametres donnes
# print(sys.argv)
if (len(sys.argv) < 4): # teste la longueur de la liste de parametres
print('il manque des arguments. Recommencez.')
exit()
elif (len(sys.argv) > 5):
print('il y a trop d arguments. Recommencez.')
exit()
#--- tout semble ok on recupere les arguments
nom = sys.argv[1]
N1 = int(sys.argv[2])
N2 = int(sys.argv[3])
option='create'
if (len(sys.argv) == 5):
if (sys.argv[4] != 'destroy'):
print('l argument 4 devrait etre: destroy? Recommencez.')
exit()
else:
option = 'destroy'
# -- recapitulatif.
if (option == 'create'):
print("Je vais creer les repertoires: "+ nom + '_{:04d}'.format(N1) + " ... " + nom + '_{:04d}'.format(N2) )
elif (option == 'destroy'):
print("Je vais detruire les repertoires: "+ nom + '_{:04d}'.format(N1) + " ... " + nom + '_{:04d}'.format(N2) )
# ---- Effectue le travail --------------------
for i in range(N1, N2+1):
nom_rep = nom + '_{:04d}'.format(i)
if(option == 'create'):
try:
os.mkdir(nom_rep)
except:
print('Le repertoire '+ nom_rep +' existe deja.')
elif (option == 'destroy'):
try:
os.rmdir(nom_rep)
except:
print('Le repertoire '+ nom_rep +' ne peut etre detruit car il est non vide.')
print('fini.')
8.2 Envoyer un mail
import smtplib
server = smtplib.SMTP('smtp.free.fr')
expediteur='toto@free.fr'
destinataire='toto@free.fr'
Message='''\
From: (Regis) regis@free.fr
To: (Toto) toto@free.fr
Subject: Profil
J'aime bien ton profil!'''
# Message (il faut laisser une ligne blanche avant le contenu message # et faire attention a la marge
try:
server.sendmail(expediteur,destinataire,Message)
server.quit()
except SMTPException as why:
print (why)
8.3 Notation musicale
8.4 Analyse de signaux audio (sur fichiers, temps différé)
Référecnes mathématiques:
- S. Mallat « A wavelet tour of signal processing »
Reference informatiques:
Some examples:
8.4.1 Play/record sound
- sounddevice : pour play/record simplement ou en temps réel.
8.4.2 Wavelett transform with scipy
Morlet2 wavelet:
For ,
Sampling. Let
So that if is even, and if is even, .
We get a list by
Mathematical wave-packet
with so that .
Sampling: for ,, , we samplewith andso that with steps and
Relation
We haveifconversely take .
Preuve.
We have and hence
and
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Sat Jan 2 09:19:29 2021
@author: faure
"""
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
#===================
#wave packet with morlet2
f = 300 # frequency
sigma = 0.01 # width
omega = 2 *np.pi * f
delta = 1/44100. # time step
t0 = 3*sigma # time interval
M = int(2*t0/delta) # size of list
s = sigma/delta
w = sigma*omega
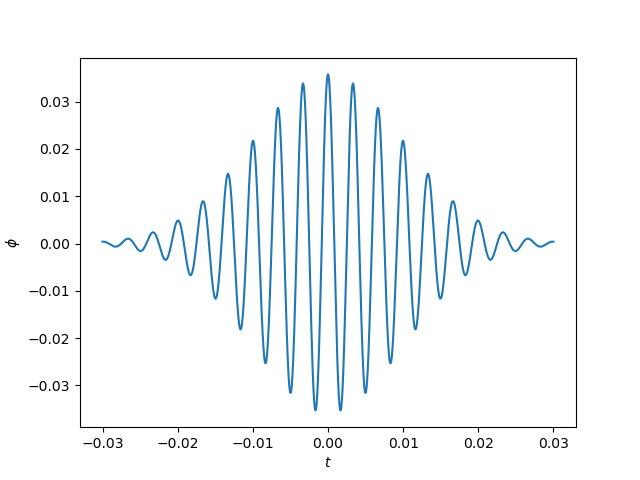
wavelet = signal.morlet2(M, s, w)
Lt = np.linspace(-t0, t0, M)
plt.plot(Lt, np.real(wavelet))
plt.xlabel('$t$')
plt.ylabel('$\phi$')
plt.show()
8.4.3 Plot a file in wav format
From this
wav file that was recorded with audacity.

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed Dec 23 17:03:59 2020
@author: faure
Plot a wav file
"""
import math
import wave
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
#=============================================
# using the module wave
# input: name of the file
# output: array with the data
def file_wav_to_array(name_file):
global n_chan, data_size, rate, N
# Read wav file
f = wave.open(name_file)
#f = wave.open("offrandes_oubliees.wav")
#informations on the sound
N = f.getnframes() # number of data
n_chan = f.getnchannels() # 1: mono, 2 : stereo
data_size = f.getsampwidth() # in octet: ex: 2
rate = f.getframerate() # ex: rate = 44100 Hz
# transfer the file to a list
L_u = f.readframes(N)
# Convert buffer to float32 using NumPy
buf_as_np_int16 = np.frombuffer(L_u, dtype = np.int16)
buf_as_np_float32 = buf_as_np_int16.astype(np.float32)
# Normalise float32 array so that values are between -1.0 and +1.0
max_int16 = 2**15
return buf_as_np_float32 / max_int16, N, rate
#======================================
# plot the signal
# input: array with the data
def plot_signal(L_u):
N = len(L_u)
t_max = N /rate
t = np.linspace(0, t_max, N) # N values equidistributed in [0,tmax]
plt.figure() # open a new window
plt.cla() # efface le graphisme precedent
plt.plot(t, L_u)
#plt.plot( L_u) # plot with data in abcisee
plt.xlabel('t(s):temps')
plt.ylabel('u(t)')
plt.title('Signal u')
plt.grid() # montre grille
plt.axis([0, 0.01, -1,1]) # selectionne la vue
plt.show() # montre le dessin
#========================================
#---- read wavefile using the module wave
#L_u, N, rate = file_wav_to_array("audio.wav") # L_u: list
#L_u, N, rate = file_wav_to_array("trumpet.wav") # L_u: list
#---- read wavefile using the module wavfile
rate, L_u = wavfile.read("audio.wav")
plot_signal(L_u)
D = 2 # duration
F= 44100 # frequency of sampling in Hz
dt = 1/F # time step
L_t = np.arange(0, D, dt) # list of discrete times
f0= 440
L_u = 0.5* np.cos(2.0 * np.pi * f0 * L_t + np.pi/4)
#---- write wavefile using the module wavfile. The maximale amplitude is 1
wavfile.write('audio.wav', F, L_u)8.4.4 Detect the pitch from a file in wav format
From this
wav file that was recorded with audacity.

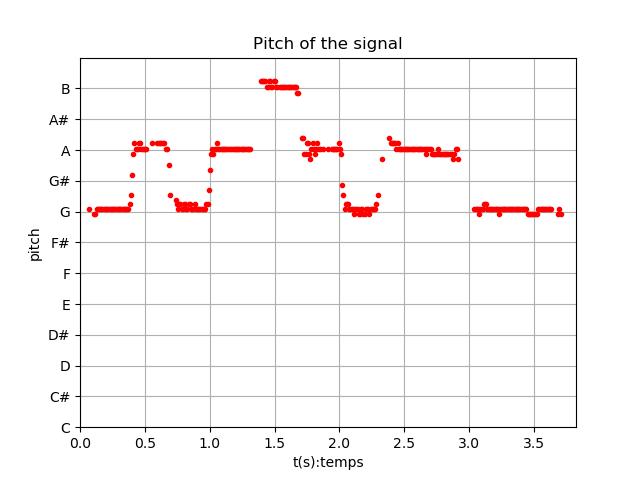
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed Dec 23 17:03:59 2020
@author: faure
Input: wav file
Ouput: pitch detect
"""
import math
import wave
import numpy as np
import matplotlib.pyplot as plt
from numpy import linalg as LA
f_A = 440 # freq of A in Hz
#=============================
def freq_to_pitch(f):
return 12/math.log(2) * np.log(f/f_A) + 69
#=============================
def pitch_to_freq(x):
return f_A * np.exp(math.log(2.)/12. * (x - 69))
#=============================================
# using the module wave
# input: name of the file
# output: array with the data
def file_wav_to_array(name_file):
global n_chan, data_size, rate, N
# Read wav file
f = wave.open(name_file)
#f = wave.open("offrandes_oubliees.wav")
#informations on the sound
N = f.getnframes() # number of data
n_chan = f.getnchannels() # 1: mono, 2 : stereo
data_size = f.getsampwidth() # in octet: ex: 2
rate = f.getframerate() # ex: rate = 44100 Hz
# transfer the file to a list
buf = f.readframes(N)
# Convert buffer to float32 using NumPy
buf_as_np_int16 = np.frombuffer(buf, dtype = np.int16)
buf_as_np_float32 = buf_as_np_int16.astype(np.float32)
# Normalise float32 array so that values are between -1.0 and +1.0
max_int16 = 2**15
return buf_as_np_float32 / max_int16, N, rate
#======================================
# plot the signal
# input: array with the data
def plot_signal(buf):
N = len(buf)
t_max = N /rate
t = np.linspace(0, t_max, N) # N values equidistributed in [0,tmax]
plt.figure() # open a new window
plt.cla() # efface le graphisme precedent
plt.plot(t, buf)
#plt.plot( buf) # plot with data in abcisee
plt.xlabel('t(s):temps')
plt.ylabel('u(t)')
plt.title('Signal u')
plt.grid()
plt.show() # montre le dessin
#=========================================
#Compute pitch
def Compute_pitch():
itau_max = 300 # size max for the shift
fmin = rate/itau_max
print("Lower frequency is :", fmin , " Lower pitch is:", freq_to_pitch(fmin))
N2 = int(N/itau_max)
C_seuil = 0.4 # seuil pour C
n2_seuil = itau_max * 1e-4 # seuil for norme n2
L_f = np.zeros(N2)
t_s = 1.8 # time selection for display
it2_s = int(t_s*rate /itau_max)
L_C_s = np.zeros(itau_max) # for display only
for it2 in range(0, N2 -2): # interval start
#print(N2-it2)
it = it2*itau_max
L1 = buf[it : it + itau_max] #extract
L3 = buf[it : it + 2*itau_max] #extract
n2 = LA.norm(L3)
C = 4;
itau_min = 0;
for itau in range(10, itau_max): # shift
L2 = buf[it+itau : it + itau + itau_max] #extract
if(n2 > n2_seuil):
C2 = LA.norm(L2-L1) / n2
if(it2 == it2_s): # for display
L_C_s[itau] = C2
if(C2 < C):
C=C2
itau_min = itau
if(C < C_seuil):
freq = rate/itau_min
L_f[it2] = freq_to_pitch(freq)
#====== plot C
plt.figure() # open a new window
plt.cla() # efface le graphisme precedent
plt.plot(L_C_s,'b.')
plt.xlabel('tau(s):time shift')
plt.ylabel('C(tau)')
plt.title('Difference')
#====== plot the pitch view
plt.figure() # open a new window
Lt2 = np.linspace(0, t_max, N2) # N2 values equidistributed in [0,tmax]
plt.cla() # efface le graphisme precedent
plt.plot(Lt2, L_f, 'r.') # red and points
plt.xlabel('t(s):temps')
plt.ylabel('pitch')
plt.title('Pitch of the signal')
plt.grid() # show a grid
xmin = 60
xmax = 73
plt.axis([0, t_max, xmin, xmax]) # select the view
plt.yticks(numpy.arange(xmin, xmax, 1)) # impose the list of labels
ay = plt.gca() # get current axis
a = ay.get_yticks().tolist() # get list of current axis
a = ['C5', 'C#', 'D', 'D#', 'E', 'F', 'F#', 'G', 'G#', 'A', 'A#', 'B', 'C6']
ay.set_yticklabels(a)
plt.show() # montre le dessin
#=============================================
buf = file_wav_to_array("flute.wav")
plot_signal(buf)
Compute_pitch()
8.4.5 Here is the code to draw a waveform and a frequency spectrum of a wavefile
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Fri Dec 18 17:57:04 2020
@author: faure
"""
import wave
import numpy as np
import matplotlib.pyplot as plt
signal_wave = wave.open('flute.wav', 'r')
sample_rate = 44100 # en Hz
sig = np.frombuffer(signal_wave.readframes(sample_rate), dtype=np.int32)
sig = sig[:] #For the whole segment of the wave file
#sig = sig[25000:32000] #For partial segment of the wave file
#left, right = data[0::2], data[1::2] #Separating stereo channels
plt.figure(1)
plot_a = plt.subplot(211)
plot_a.plot(sig)
plot_a.set_xlabel('sample rate * time')
plot_a.set_ylabel('energy')
plot_b = plt.subplot(212)
plot_b.specgram(sig, NFFT=1024, Fs=sample_rate, noverlap=900)
plot_b.set_xlabel('Time')
plot_b.set_ylabel('Frequency')
plt.show()8.5 Audio en temps réel
8.5.1 Exemple d'enregistrement en temps réel.
import pyaudio
import numpy as np
CHUNK = 2**10
RATE = 44100
p=pyaudio.PyAudio()
stream=p.open(format=pyaudio.paInt16,channels=1,rate=RATE,input=True, frames_per_buffer=CHUNK)
for i in range(int(10*RATE/CHUNK)): #go for a few seconds
data = np.fromstring(stream.read(CHUNK),dtype=np.int16)
peak=np.average(np.abs(data))*2
bars="#"*int(50*peak/2**16)
print("%04d %05d %s"%(i,peak,bars))
stream.stop_stream()
stream.close()
p.terminate()
Avec dessin:
import pyaudio
import numpy as np
import matplotlib.pyplot as plt
CHUNK = 2**10 # 1024 buffer size
RATE = 44100 # frequency of sampling
p = pyaudio.PyAudio() # nouvel objet p de la class PyAudio
stream = p.open(format = pyaudio.paInt16, channels=1, rate=RATE, input=True, frames_per_buffer = CHUNK)
for i in range(1000):
plt.cla() # efface le graphisme precedent
T = np.fromstring(stream.read(CHUNK), dtype=np.int16)
plt.plot(T)
plt.axis([0, 1024, -32000, 32000]) # selectionne la vue
plt.pause(0.001) # montre la figure et attend 0.001 sec.
stream.stop_stream()
stream.close()
p.terminate() Utilisant La capture audio dans un thread séparé:
#May 2020
import pyaudio
import numpy as np
import matplotlib.pyplot as plt
import time
CHUNK = 2**11 # 2**11 = 2048 buffer size
RATE = 44100 # frequency of sampling
p = pyaudio.PyAudio() # nouvel objet p de la class PyAudio
"""
this function is called on a separate thread for each new buffer on audio input
input: in_data: the input data
frame_count: taille du tableau = CHUNK
"""
def audio_event(in_data, frame_count, time_info, status):
global T
T = np.fromstring(in_data, dtype=np.int16) # transforme en tableau de chiffres
return (in_data, pyaudio.paContinue)
#----------------------------------------------
stream = p.open(format = pyaudio.paInt16, channels=1, rate=RATE, input=True, frames_per_buffer = CHUNK, stream_callback = audio_event)
stream.start_stream() # lance la fonction audio_event() dans un autre thread
while stream.is_active():
plt.cla() # efface le graphisme precedent
time.sleep(0.1)
plt.plot(T)
plt.axis([0, 1024, -32000, 32000]) # selectionne la vue
plt.pause(0.001) # montre la figure et attend 0.001 sec.
stream.stop_stream()
stream.close()
p.terminate()
8.6 Acquisition avec PyVisa
Chapitre 9 Librairie PyRoot pour le graphisme et l'analyse de données
Chapitre 10 Librairie opencv pour l'analyse d'images
10.1 Lecture et ecriture de fichiers images
Les commentaires expliquent les fonctions. Il faut avoir le fichier
Image.jpg dans le répertoire du programme.
Ecrire:
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
#..... Lecture d'une image -> img
img = cv.imread('Image.jpg')
#..... dessin de l'image img en utilisant opencv
cv.imshow('Titre',img)
#..... dessin de l'image img en utilisant matplotlib
plt.imshow(img, cmap = 'gray', interpolation = 'bicubic')
plt.xticks([]), plt.yticks([]) # to hide tick values on X and Y axis
plt.show()
#...... Ecriture d'une image: img -> fichier Image2.jpg
cv.imwrite('Image2.jpg',img)
#..... Lecture d'un pixel
x=img.shape[0]/2 # selectionne point (x,y) au centre de l'image
y=img.shape[1]/2
p= img[x,y] # valeur du pixel
print('La valeur du pixel en x=',x,', y=',y,' est (B,G,R): (',p,')')
#..... Attend qu'une touche soit appuyee.
c = cv.waitKey(0) # rem: montre le dessin. Renvoit le code de la touche. On peut mettre une duree t en ms. ex: 2000
Resultat:
- Affiche deux images: une en couleur et l'autre en noir et blanc.
- Pixel value (B,G,R): (3,7,12)
10.2 Video
Ecrire:
import numpy as np
import cv2
cap = cv2.VideoCapture(0)
while(True):
# Capture frame-by-frame
ret, frame = cap.read()
# Our operations on the frame come here
gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
# Display the resulting frame
cv2.imshow('frame',gray)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
# When everything done, release the capture
cap.release()
cv2.destroyAllWindows()
10.3 Références sur Opencv with python and deep-learning
10.3.1 Installations
10.3.2 Exemples
10.3.3 Object detection with pretrained models
10.3.3.1 with YOLO algo
10.3.3.2 with opencv::dnn module and SSD (Single Shot Detectors) and MobileNets algos.
10.3.4 Quelques articles d'algorithmes de deep learning
10.3.5 DataBase
10.3.6 Utiliser Coral de Google
10.3.7 Différents modèles
10.3.8 Create a GUI for opencv
10.3.9 Sites web
Chapter 11 Python virtual environments
permet de travailler avec des versions spécifiques pour un projet donné.
Creation d'un envirronement appelé cv:
mkvirtualenv cv -p python3
Lancer l'environement:
workon cv
Se deconnecter:
deactivate
On peut installer des librairies, par ex:
pip install numpy
Chapitre 12 Librairie Caffe pour le deep Learning (DL)
12.1 Deep learning
12.1.1 The model
Let the function « sigmoid »:so that , .
We extend to (keeping the same notation) by
Let an affine map, i.e.with and linear.
Définition 12.1.1.
A « Layer » is a map of the formA layer map is given bywith layer maps .
12.1.1.1 Training datas
Suppose that we have a set of « data points »with in the initial space and in the final space, called the « answer ». Usually can have two values.
12.1.1.2 Cost function
Définition 12.1.2.
For a given map
as above and training datas
, we associate the « cost » or « objective »
12.1.1.3 Training problem or optimization problem
For given datas , find the map (in a connected component, i.e. only parameters of ) that minimizes :
12.1.2 Algorithm of gradient flow
A problem is to compute .
Gradient flow is the flow generated by the gradient vector field on the space of all maps, equation of motion is
12.1.2.1 Computation of
We havewithandParameters of are with .
Hencewith
12.1.2.2 « stochastic gradient » method,
Numerically it is usual to apply the « stochastic gradient » method, which consists in:
- discretize time in small steps .
- Repeat many times:
- choose some randomly and compute
- apply the modification
Chapitre 13 Deep learning
13.1 Using Coral USB Accelerator with tensorflow Lite
Chapitre 14 Convertir python en javascript
Documents:
 a
a