Movies and pictures
Notice:
- “Movies” are animated gif. If you use browser Firefox, we advice you to install plugin "Toggle animated GIFs" and use keys :
- "Shift+M": to start again the movie
- "Ctrl+M": to stop/continue the movie
Objective: describe “emergent behaviors” in “complex dynamical systems”.
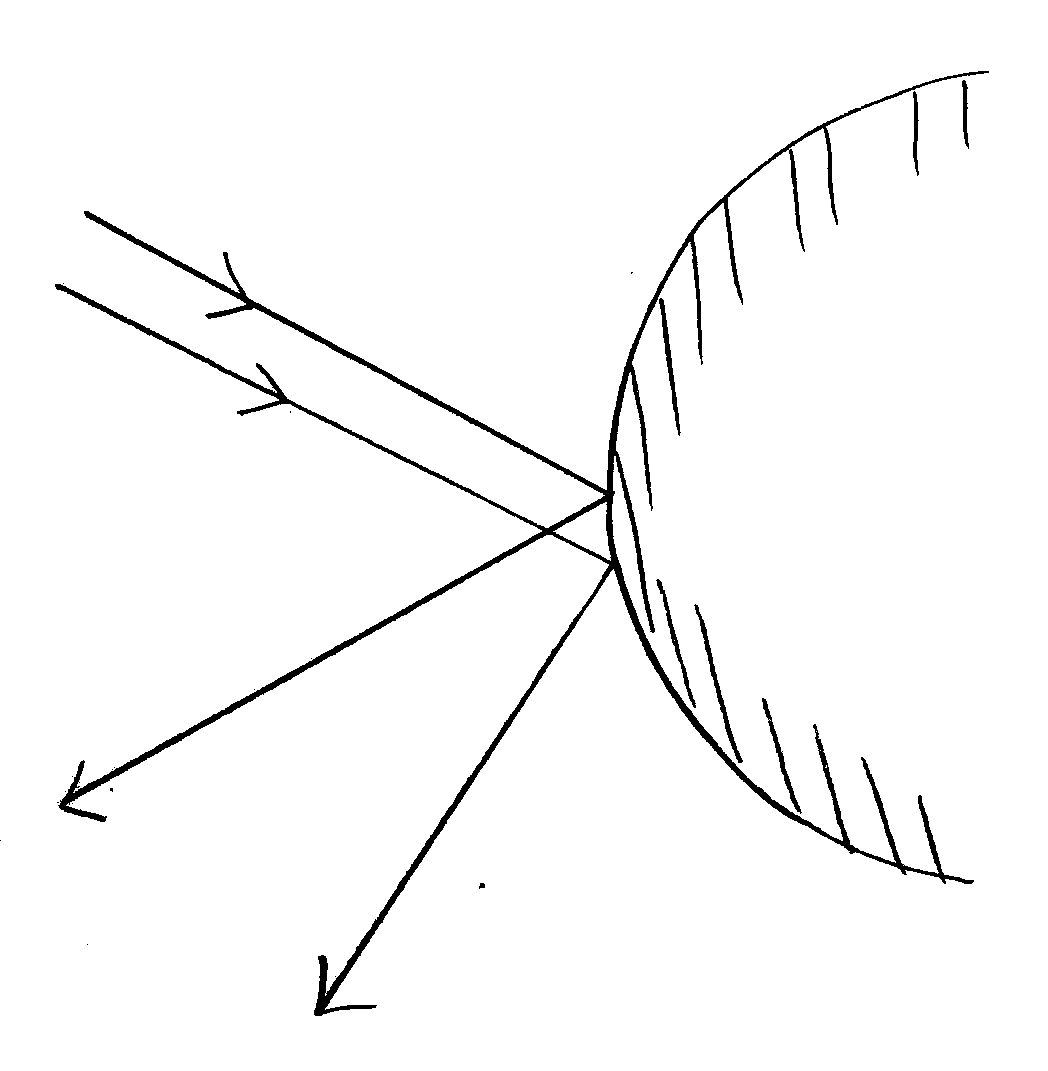
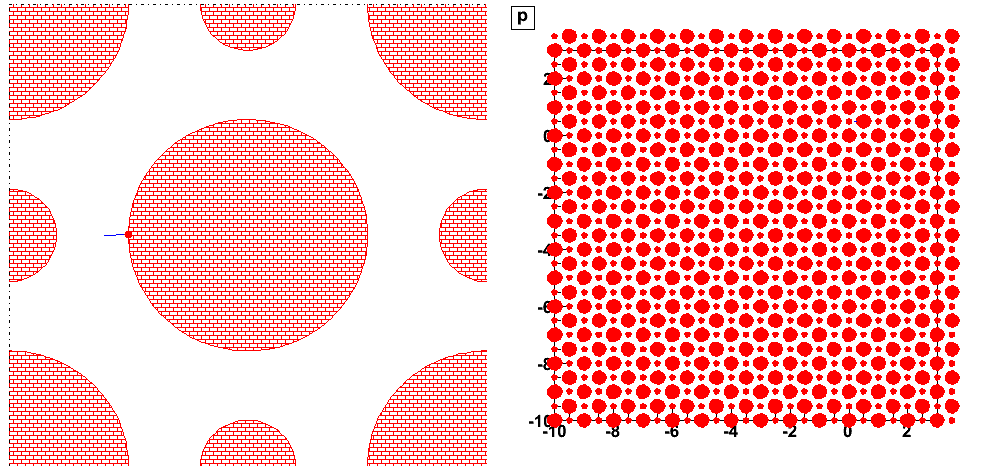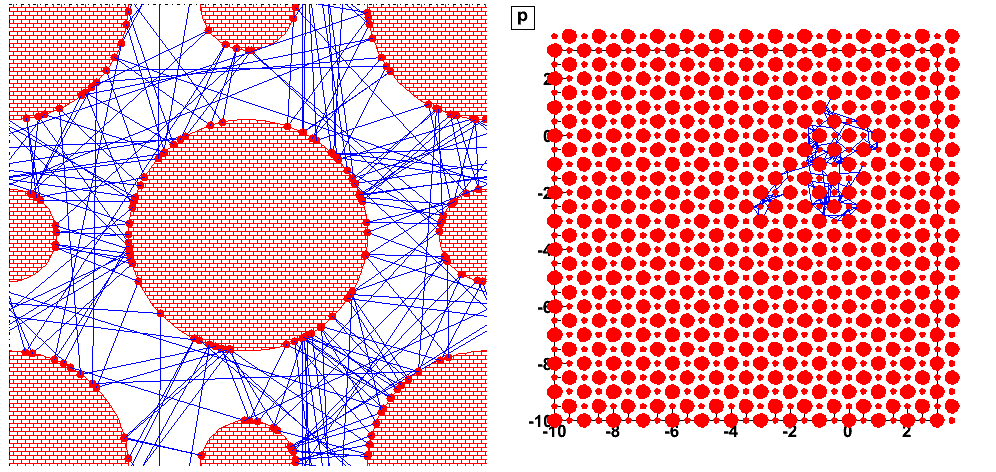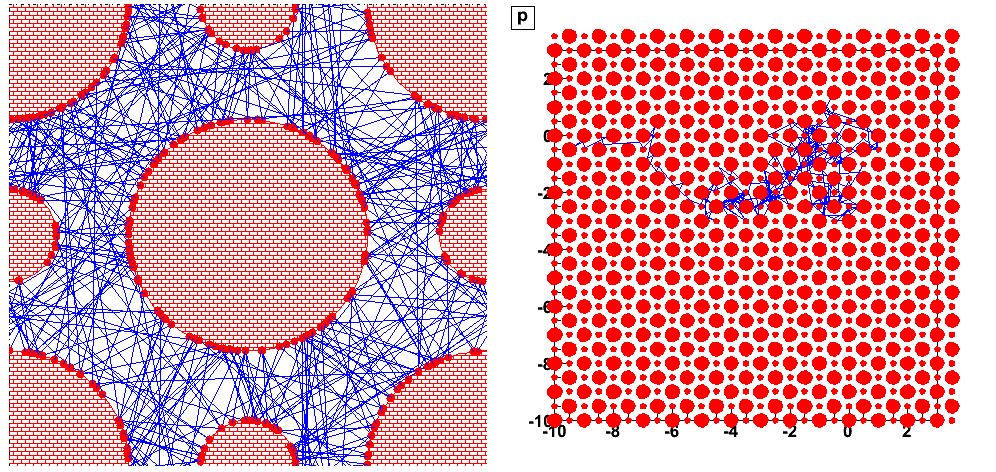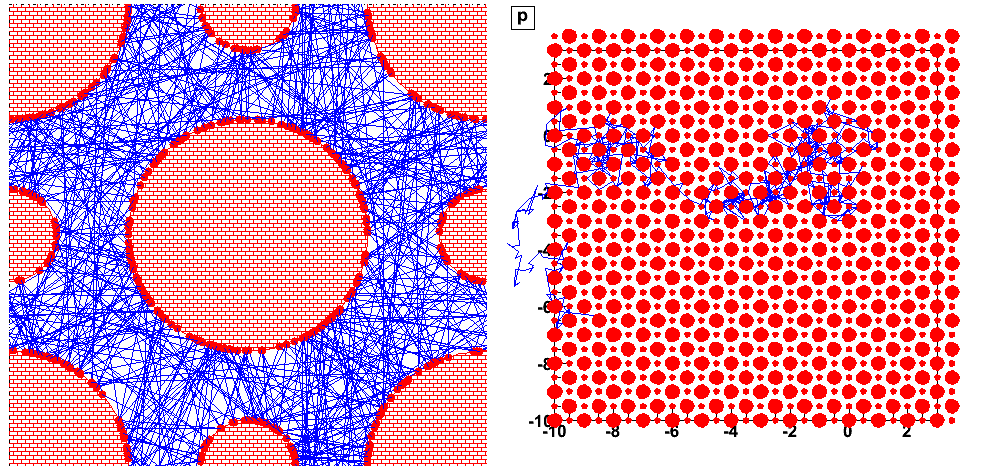
1 Dynamics in a Sinaï billard (with finite horizon)
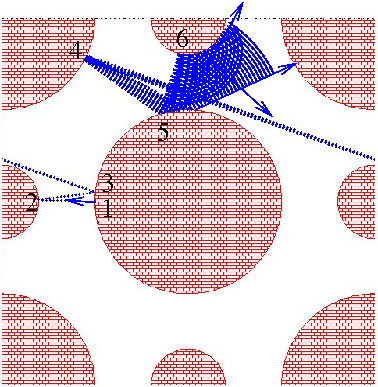
At each bounce there is “dispersion of trajectories”:
This is the limit case of the geodesic flow on a surface with negative curvature:
We observe an unpredictable, chaotic behavior of an individual trajectory (but reversible):
Trajectories starting from closed initial conditions (), have very different behaviour after few bounces only (they become decorrelated).
Observe through a smooth observable , the evolution of a smooth distribution of probability , i.e.
The distribution is represented here by independent points with closed initial conditions .
Colors of directions:

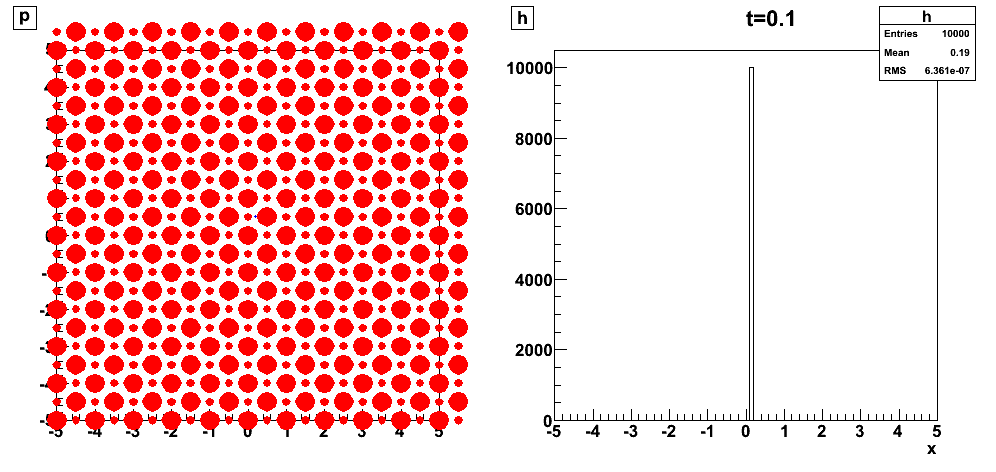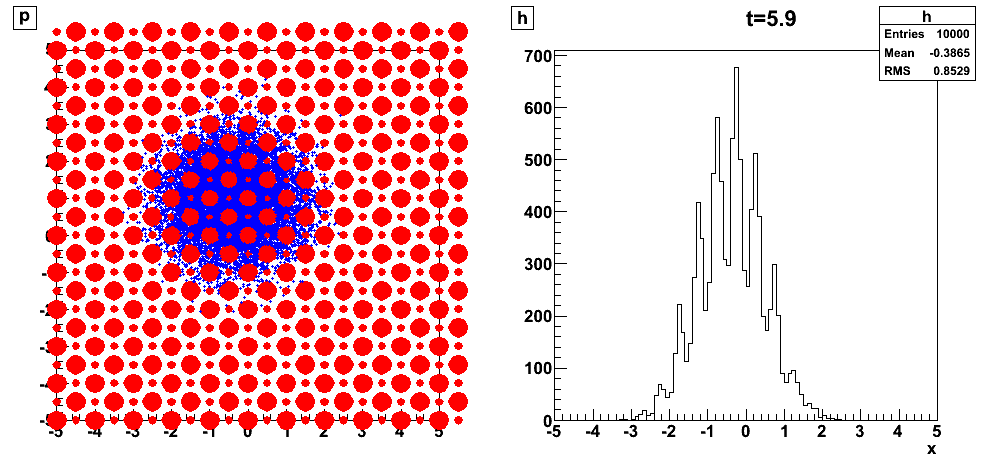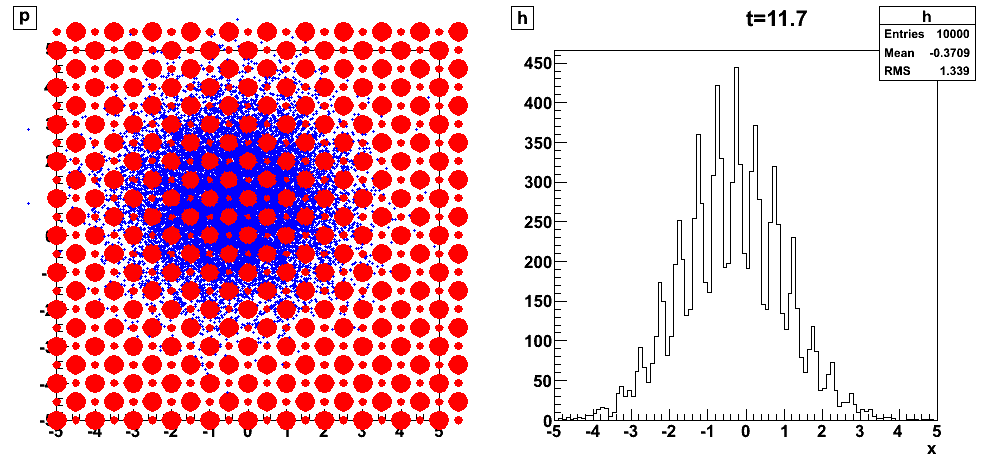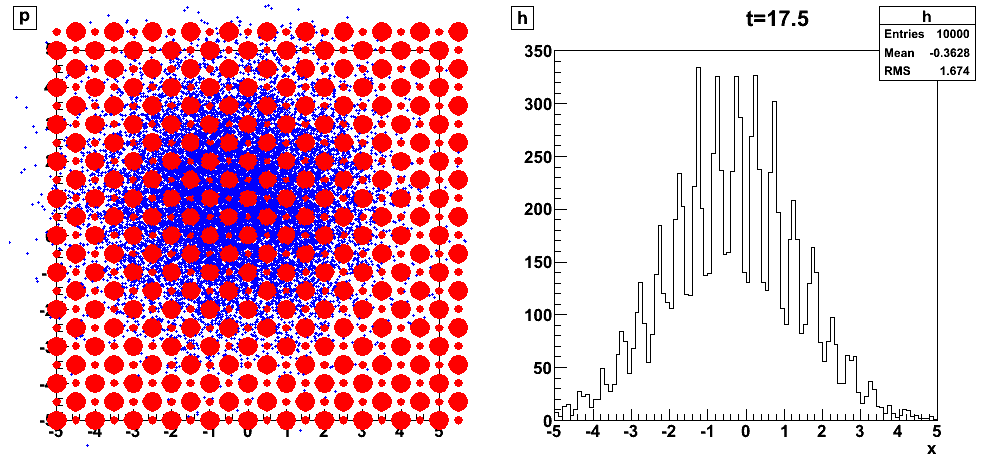
We observe a predictable but irreversible behavior:
Statistical laws emerge (diffusion):
Information escapes to microscopic scales escapes to high Fourier modes:
irreversibility at macroscopic scales, the entropy increases.
Emergent effective dynamics of fluctuations that we want to characterize.
Analogy: with the escape of quantum waves outside the nucleus (radioactive decay), or photon outside an excited atom (fluorescence). Stationnary decaying states are called meta-stable states, “resonances”. The decay of correlation functions and fluctuations is characterized by the discrete spectrum of resonances (not in ).
Studied in physics and semiclassical analysis (Combes 70', Helffer-Sjöstrand 80')
Results: (F.-Tsujii, 2013-2016).
For an Anosov geodesic flow, the emergent dynamics (correlation functions) is governed by a discrete spectrum of Ruelle resonances that concentrate on a vertical axis, and a wave equation or emergent Schrödinger equation that describes the fluctuations of the distribution.
This spectrum is determined by closed orbits, zeros of a Gutzwiller-Voros zeta function that generalizes Selberg zeta function to non variable curvature manifolds.
2 Partially expanding map
Model:Transfer operator:
Reduced transfer operator to Fourier mode :