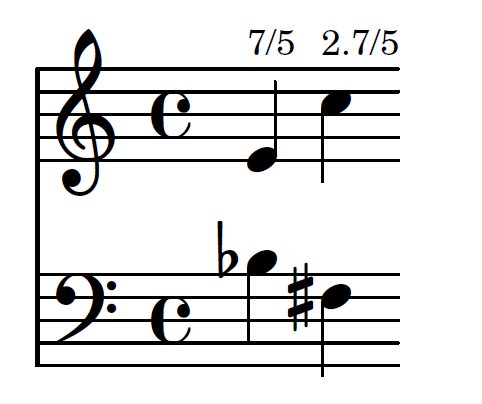Voix chantée, mathématiques et musique.
(Perception auditive de l'arithmétique (?)).
Remarques
c'est un document “multimédia”,
- Il y a des fichiers sonores, il faut cliquer sur l'icône “Son”. Il est préférable de cliquer avec le bouton droit et de choisir “ouvrir le lien dans une nouvelle fenêtre” que l'on fait de petite taille.
- Il y a des fichiers vidéo, il faut cliquer sur l'icône “Video”. Il est préférable de cliquer avec le bouton droit et de choisir “ouvrir le lien dans une nouvelle fenêtre” que l'on fait de petite taille.
- Il y a des liens vers des sites extérieurs, notamment vers wikipedia.
1 Introduction
- C'est un thème de recherche qui date au moins depuis l'antiquité (Babylone, Pythagore, Euclide,...), avec encore de nombreuses questions.
- Voici une présentation générale du sujet, liée à un travail de “recherche”. Il y a des interprétations (spéculations) personnelles, notée par (?). Collaboration avec Malik Mezzadri (artiste musicien “Magic Malik”) et Alexandre Ratchov (informaticien). Concerts avec Jean Luc Lehr (basse fretless) et Maxime Zampieri (batterie et touchpad).



- Références:
2 Voix chantée et audition. Séries de Fourier.
2.1 Origines
La voix est apparue entre -
millions d'années (sons),
ans (parole) pour palabrer et pour l'échange d'informations (?).
2.2 Émission de la voix
- Les cordes vocales qui génèrent une vibration (oscillateur entretenu par le souffle):
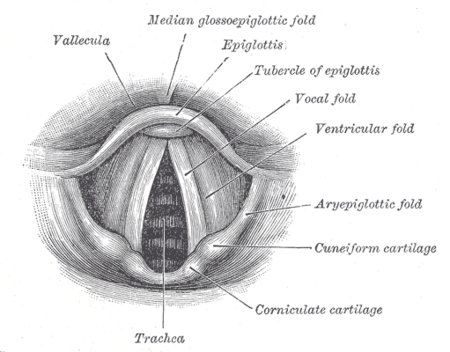
Video des cordes vocales.
Ce son “riche en fréquences” est “sculpté” par la cavité buccale pour former le
“timbre” (choix des voyelles).
Video .
2.3 Propagation de la voix
- Par exemple pour des voyelles , chantées par Malik, Son.
- l'amplitude est Atm.
- la fréquence Hz (Do), vitesse du son: donc la longueur d'onde est .
- Le signal (mesuré avec un micro) est (presque) périodique: “ON” et “A”:
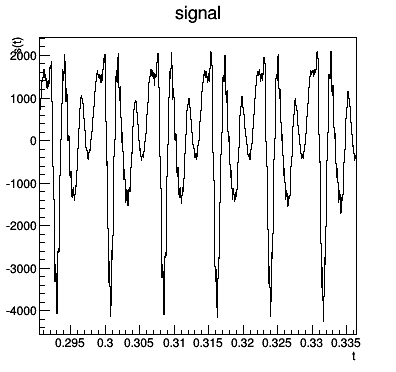
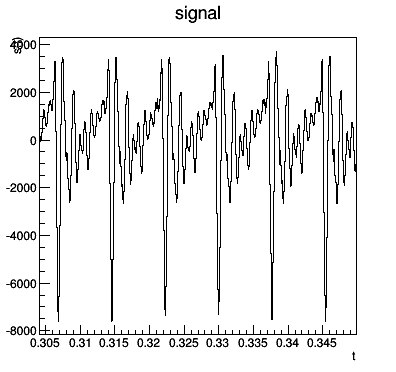
2.4 Réception
Video de la cochlée aux cellules ciliées par R Pujol, S Blatrix.
- Dans la cochlée, il y a 13000 cils , (ici échelle = ):
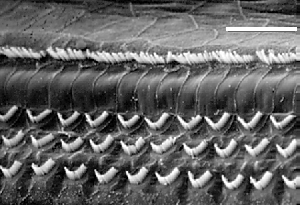
qui transmettent une excitation au cerveau (puis traitée par des réseaux de neurones, mais c'est encore mystérieux)
- Video sur la perception de la musique de Bach dans la cochlée.
- Chaque cil est un résonateur sensible à une fréquence propre entre et . Donc comme dans la théorie des séries de Fourier (1822), la voix (signal périodique ) est décomposée en “sons purs” (sinus ou “harmoniques”), et l'on détecte l'intensité de chaque harmonique (i.e. le module du coefficient de Fourier et non pas sa phase).
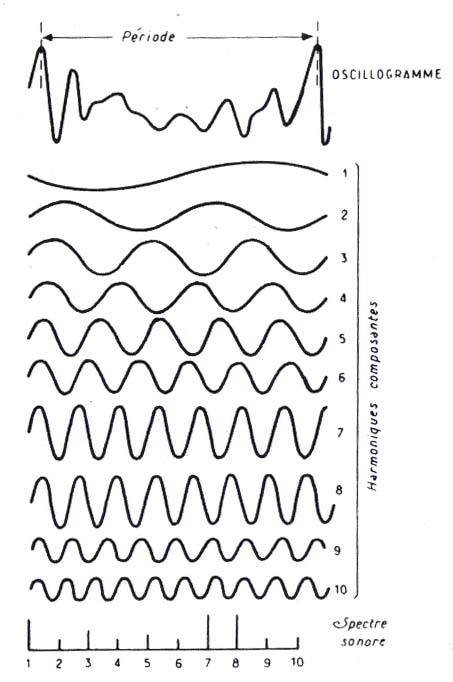
Ce
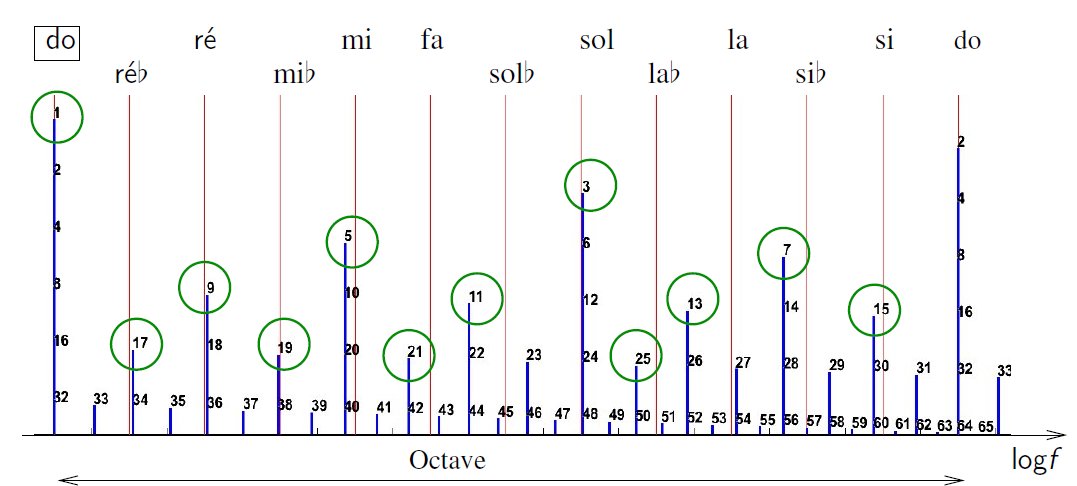
spectre d'harmoniques coïncide à peu près avec les notes musicales (ce sera expliqué après):
Même figure mais en “échelle log” ce qui correspond au clavier du piano:
- Voyelles chantées par Malik. Harmoniques et notes correspondantes. Video
- On ne détecte pas la phase des harmoniques:
- si on déphase indépendament les composantes de Fourier alors la forme d'onde très différente mais la différence est inaudible: Son de la voix sans phases. (Son original).
- Voyelle “on”, voici les formes d'ondes d'origine et déphasé et les modules coefficients de Fourier pour (qui sont inchangés):
- Voici un autre exemple de son artificiel, où chaque harmonique a un module et une phase aléatoire. On représente aussi la forme d'onde . Remarquer que lorsque les phase sont nulles, le signal est en “dent de scie”. On le percoit légèrement. Video.
- Cela signifie que “au départ” (avant traitement), le cerveau perçoit des notes pures quasi-indépendantes. A la “sortie”, on a conscience de la voyelle et de la hauteur de note (le pitch ). Que se passe t-il dans le cerveau?
- La perception des voyelles n'est pas dans les premières harmoniques:
- Video filtré avec les harmoniques 1,2,3: on n'entend plus les voyelles.
- “Le mystère de la fondamentale manquante”:
- Video filtré avec les harmoniques 5,6,7,8..: on entend les voyelles. On perçoit et la fondamentale (le “pitch” ou la période)! Le cerveau reconstruit l'illusion de la note (fondamentale)!? C'est encore un mystère pour les neurologues (). Le cerveau calcule le “pcdg” des fréquences présentes? Utilité possible (?): reconnaître l'appel de son enfant qui est parmi d'autres enfants.
- Illusion auditive:
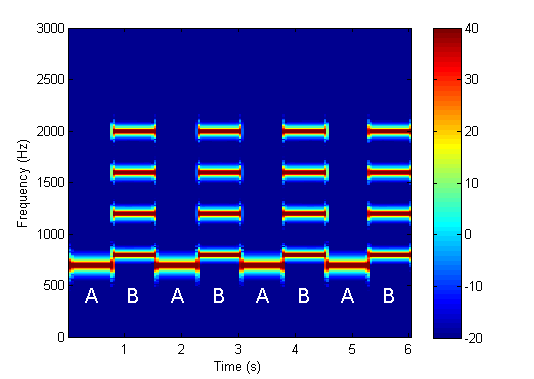
Son.
- Perception des fréquences
- Fréquences aléatoires: Voici un exemple artificiel, où les harmoniques sont d'amplitude , de phase nulle, et de fréquence avec Hz (do) et aléatoire. On représente sur ce diagramme pour différentes valeurs de qui mesure la fluctuation des fréquences. Video. Remarquer que l'on percoit parfois plusieurs notes (par exemple pour ). Remarquer que les pics de fréquences peuvent se croiser si .
- Amplification d'une harmonique (chant diphonique des mongols):
Si une harmonique est “trop” amplifiée alors elle ressort du timbre (de la perception collective) et on l'entend consciemment.
Ex: Harmoniques 6 à 12:

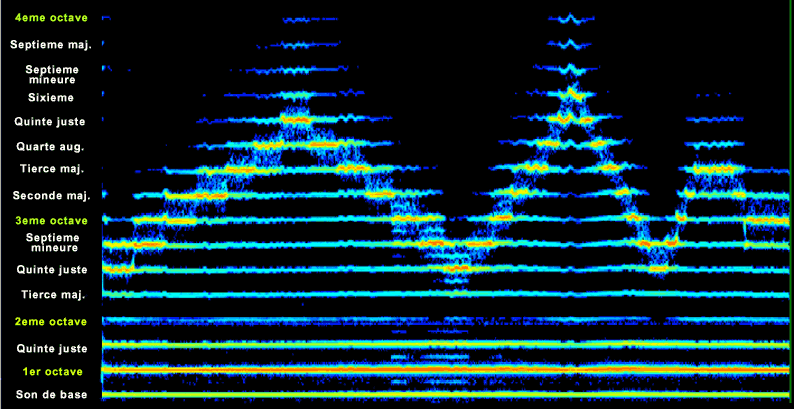
Son
- Video de Ana-Maria Hefele à 4mn.
- Résumé:
- A la sortie des oreilles, et à l'entrée du cerveau, on a effectué (inconsciemment) une décomposition du son en “notes pures” (mode de Fourier). Ensuite le cerveau effectue un “traitement complexe” de cette information. [2, p.138] (dans le cerveau il y a un processus de reconnaissance de pattern arithmétique?)
- Au final on est conscient de l'ensemble du spectre: “le timbre” et son “pitch” (fondamentale), et non pas des fréquences individuelles.
Références
2.5 Instruments de musique
Ils permettent aussi de générer un signal sonore périodique (imitation de la voix chantée) par un mécanisme physique adéquate. Souvent une oscillation entretenue.
- Pour les flûtes, ou sifflets, le biseau crée des tourbillons périodiques. Pour la trompette, les lèvres vibrent. Pour les saxos, l'anche vibre. Pour les violons, l'archer entretient l'oscillation des cordes; etc...
- Video montrant le spectre d'harmoniques de plusieurs instruments jouant la même note C4.
- Video (stroboscopique) des cordes d'une guitare (nicogetz youtube).
- Video des modes de vibration d'une corde pincée ou frappée.
3 Intervalles de musique, fractions rationnelles.
- Rappel: pour une note individuelle (voix ou instrument), on ne perçoit pas ses harmoniques individuelle, mais on perçoit le timbre qui est une impression collective, interprétée par le cerveau.
- Question: que perçoit-on si deux notes (timbrées) de fréquences sonnent ensemble?
3.1 Expériences
- Video qui montre une résonance à l'unisson .
- Video qui montre une résonance à l'octave .
- Video qui montre une résonance à la quinte .
- Video qui montre les résonances importantes.
- Video qui montre les résonances dans l'ordre descendant.
- Video qui montre les résonances avec le rajout de la “basse” . (la fondamentale manquante en rouge)
- Video qui montre les résonances avec la “basse” en rouge et le “sifflet” en vert.
- Résumé: un intervalle juste est un ensemble de deux notes dont le rapport des fréquences est avec petits entiers. On ressent cet intervalle comme “résonant” ou “consonant”.
- Schéma des rapports de fréquences résonants , leur résonance et comparaison avec la gamme tempérée ou tempérament égal, (traits bleus, utilisée pour les instruments occidentaux):
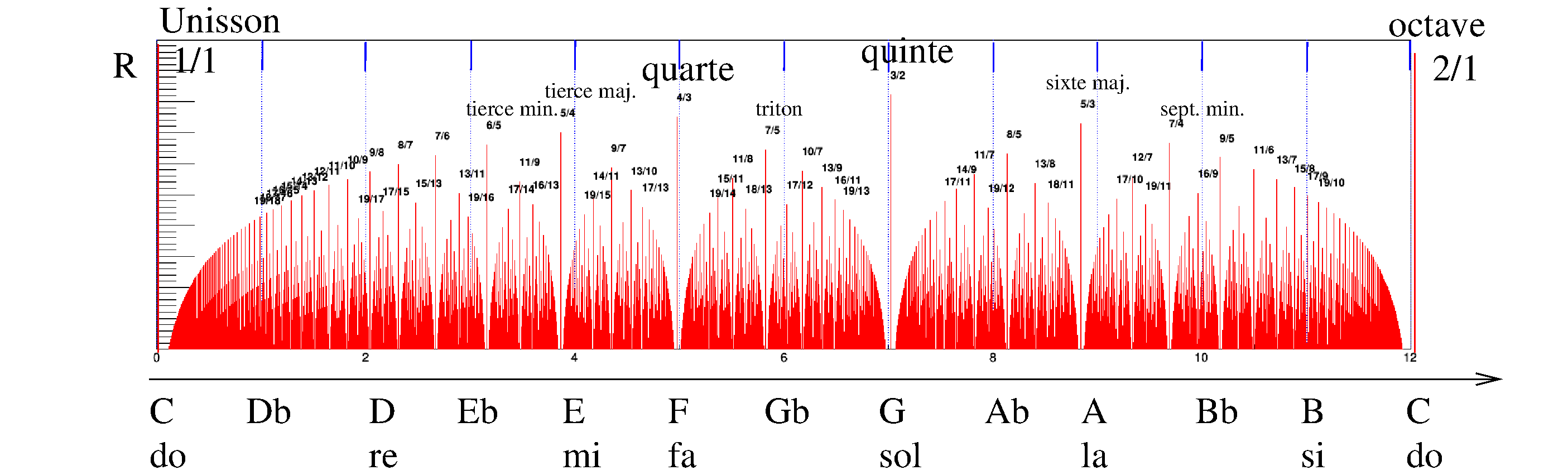
Cela forme une fractale (de Farey ou Thomae).
3.2 Dans la culture musicale
- Par ex. l'octave , la quinte , la quarte , sont des intervalles universels dans les cultures humaines. La quarte est le premier intervalle de la marseillaise. Son ou Son:

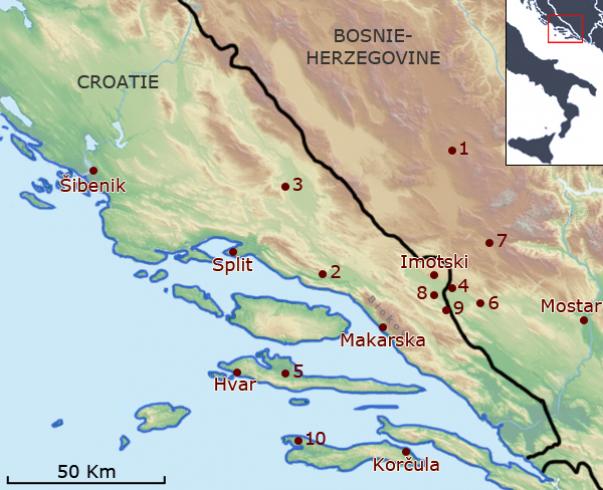
- Dans la fractale, observer les “gaps” près des fractions simples: on y trouve des intervalles “dissonants”. Par exemple, la ganga en Dalmatie: chants populaires, avec intervalles de notes qui “frottent” (pour le plaisir), ref: carnet de voyage avec Anne-Florence Borneuf. Son

- Organum est un genre musical à deux voix, du IXème au XIIème siècle en Europe, constitué d'octaves (), quintes et quartes . Les tierces et sixtes peuvent être entendues à partir du XIème siècl. ref: Musica Enchiriadis. C'est l'origine du contrepoint.
Video de Organum duplum : Alleluia, hic Martinus (“organum fleuri”).
- L' intervalle 7/5 qui est “isolé” dans la fractale, est revisité par les bee boppers (Charlie Parker, Dizzy Gillespie .., 1940'), par ex. dans l'introduction de “salt peanuts”, (intervalle quinte diminuée , puis ou ?, puis l'octave ) 1942.Son
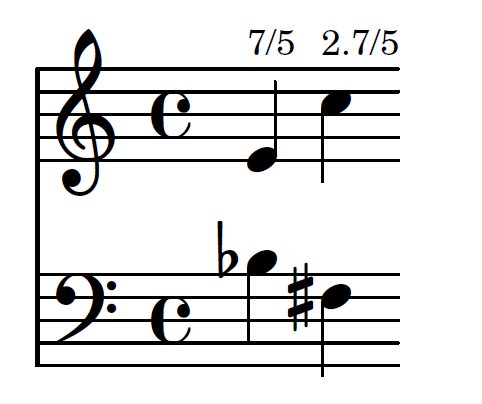

- Chants bulgares (musique traditionnelle actuelle). “Résonances ” entre des voix très timbrées (cad riches en harmoniques) qui se concluent par des unissons. Rythme en 2+2+3=7. Video.
- En musique indienne, on apprécie les résonances entre la tampura (riche en harmoniques) et la flûte.

- On entend des relations entres les notes et pas seulement avec la basse fixe (tampura). (résonances en noir, proximité de hauteur en rouge). On discute de cela après.
- Qu'observez vous sur le ré (qui est peu joué)? réponse: c'est le seul dont le dénominateur de la fraction (ici ) n'est pas une puissance de . On verra plus loin que si le musicien joue le ré de façon trop insistante, il ressort une couleur “mineur” qui n'est peut être pas voulue ici. (?)
- Video
- Intervalle et dans les chants suisses, et cor des alpes. Son (avec la “11#” à 45'', et la “13” à 1'56''). Remarquer que les musiciens évitent soigneusement de jouer l'harmonique et .


3.3 “Théorie” musicale sur les intervalles
- La théorie musicale de pythagore (à la suite des babyloniens) ne considérait que les intervalles construits à partir . Ex: . Contre-exemple: . D'après la figure suivante, cette théorie permet de décrire très peut d'intervaller résonants.
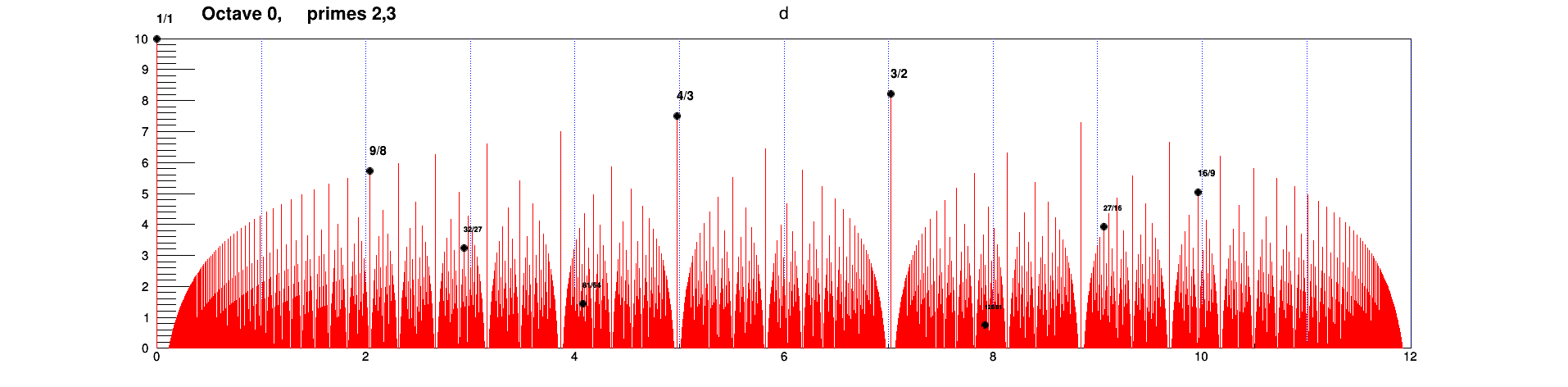
- La théorie musicale de Zarlino (1558) ne considérait que les intervalles construits à partir . Ex: . Contre-exemple:
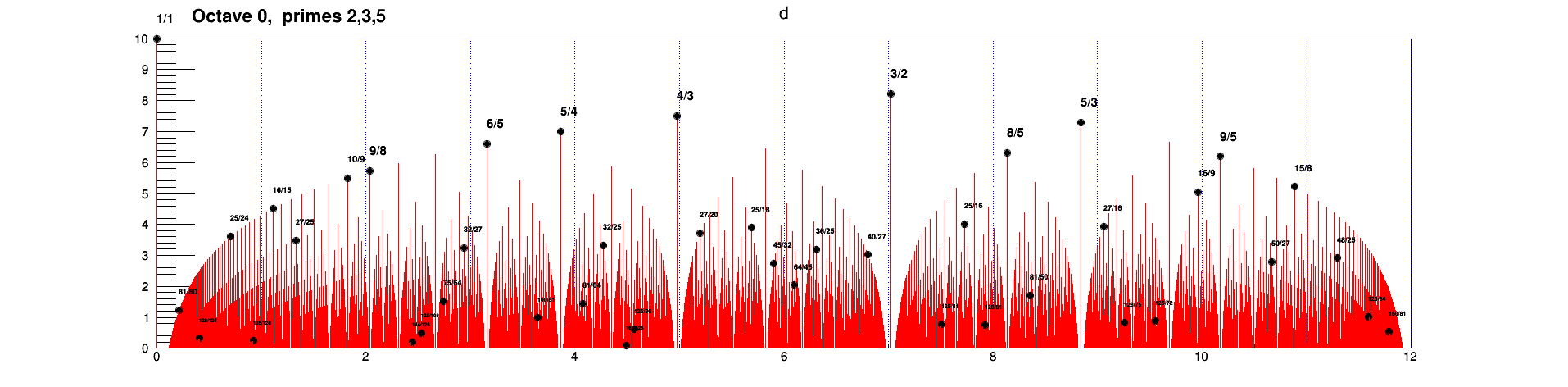
- J.P. Rameau, “Traité de l'harmonie” (1722), qui est encore une référence, écrit p.xv que la musique repose sur les chiffres seulement. Page 4 il exclut le nombre 7 car “ne pouvant donner aucun intervalle agréable, c'est évident aux connaisseurs”:


- Pourtant, les nombres ont une importance dominante dans les intervalles plus grands d'après la figure suivante pour les intervalles compris entre 1 et 2 octaves:
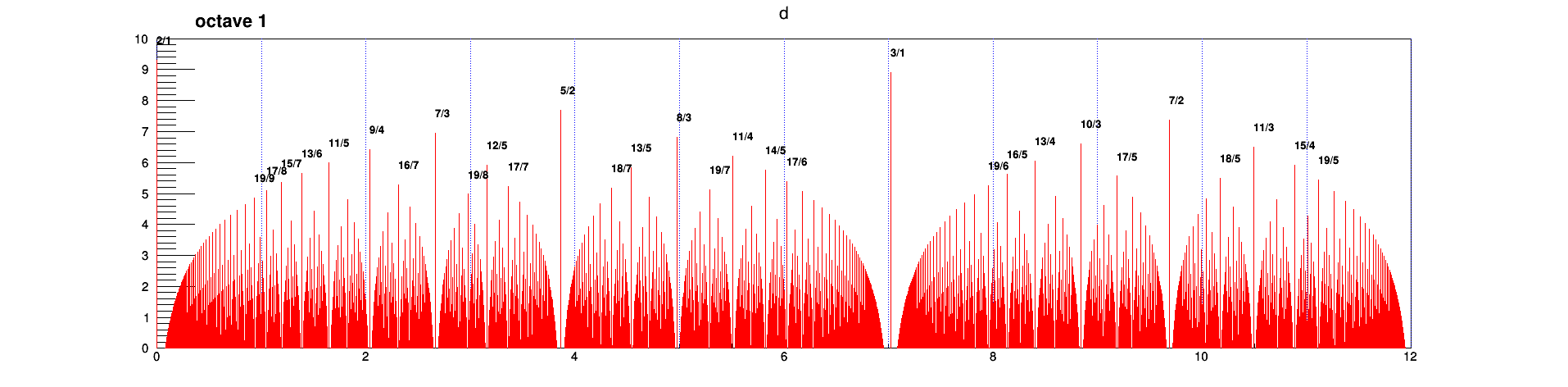
- et pour les intervalles compris entre 2 et 3 octaves:
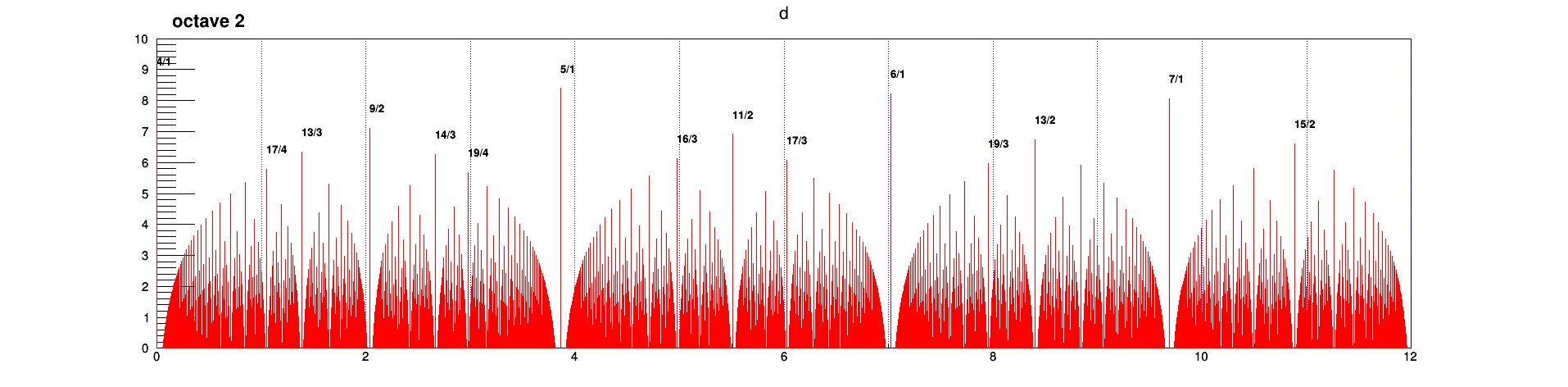
- Ces rapports ou en “quarts de tons”, semblent être utilisés en musique arabe. (?)
- Humour: sketch de Kammelott (Alexandre Astier). On entend l'unisson , quarte , quinte , tierce mineure , quinte diminuée appelé “Diabolus In Musica” au moyen âge par Guido d'Arezzo 1050(?) (reference). Video.
4 Plusieurs notes: accords et enchaînements harmoniques.
- Rappel: un intervalle juste est un ensemble de deux notes dont le rapport des fréquences est avec petits entiers. C'est un intervalle ressentit comme “consonant”.
- Question: comment décrire un accord de 3 notes (ou plus) simultanées?
- Première idée: pour généraliser la fractale de Farey/Thomae ci-dessus, pour notes , on représente la densité de résonance:Cela donne la fractale suivante où chaque point brillant est un accord (plus ou moins) résonant:
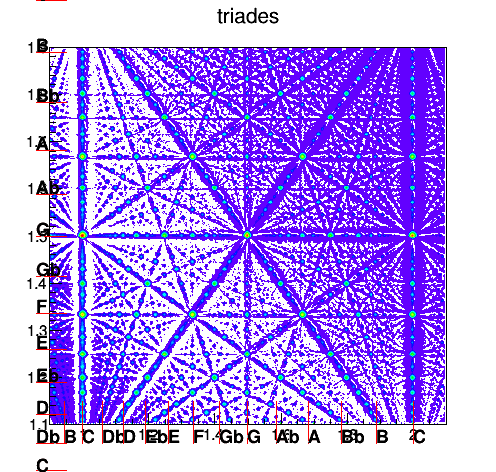
Mais cela ne semble pas très utile...(?)
- Idée naturelle de Euler (1739, il a 24 ans), dans “Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae”, représentation des intervalles sur le tonnetz (= “réseau des notes”):

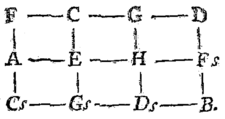
Une fraction se décompose de façon unique avec les nombres premiers sous la forme: .On représente les exposants:
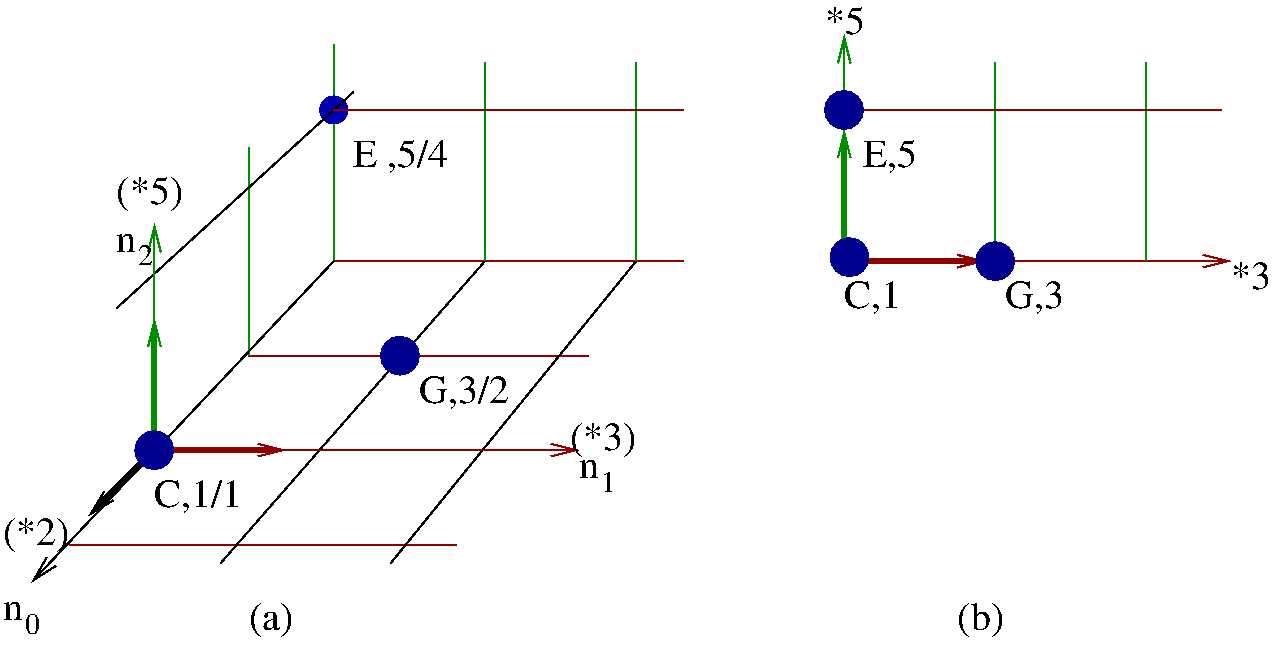
et si on oublie l'axe du
qui est l'octave, cela permet de représenter l'exposant du
:
- Un accord juste est un groupe de notes sur le tonnetz. Il est bien résonant si les notes sont regroupées sur le tonnetz (comme une molécule).
- Pour les mathématiciens, remarquer que la fonction résonance de est simplement une “norme l1 à poids” sur le tonnetz (cela donne une distance de Manhatan sur le tonnetz):
- Exemples:
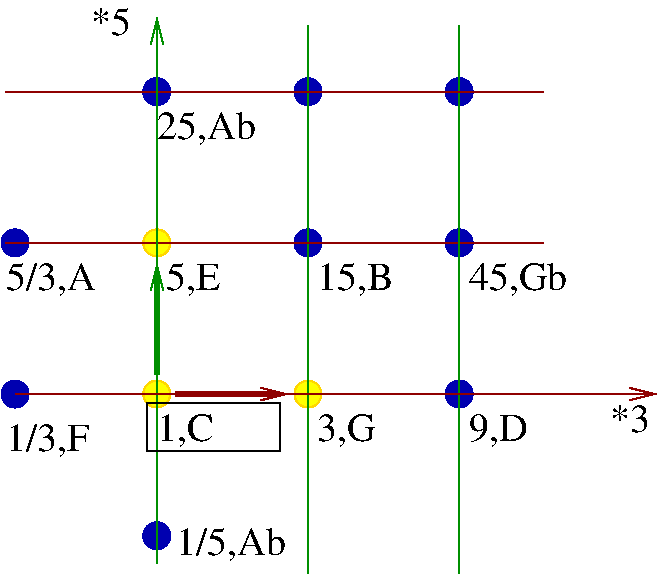
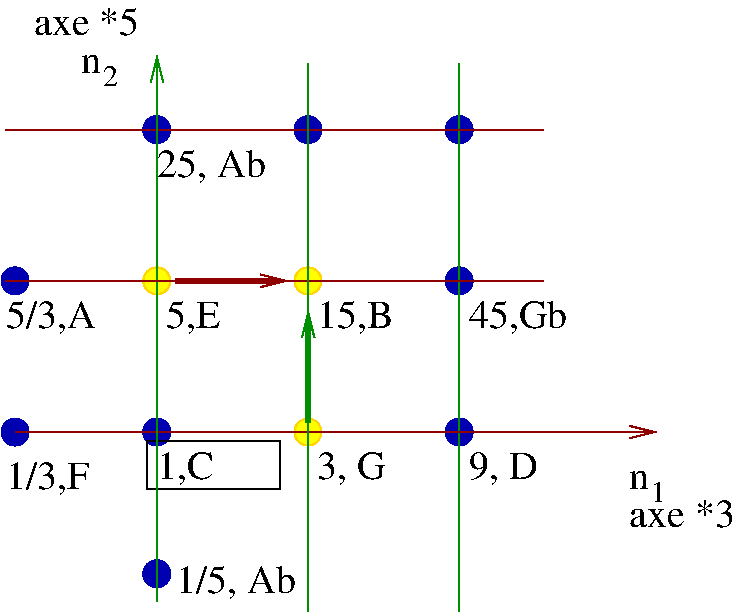
- la triade majeure C,E,G possède sa basse virtuelle qui est C. sensation de stabilité. Video
- la triade mineure Em=E,G,B n'a pas sa basse virtuelle qui est C. sensation de manque. Video
4.1 Enchaînement d'accords
- “Résolution du triton ” vers la tierce majeure : il y a un mouvement d'un demi-ton de (en tirets bleus) dont la fraction est . Il y a aussi un mouvement d'un demi-ton (en pointillés rouges) dont la fraction est . (On rappelle que le demi-ton chromatique est ). En musique ce dernier mouvement s'appelle “ résolution de la sensible”.
Video, et avec la basse virtuelle: Video.
- (Cadences II-V-I Majeure: Video et mineure Video.)
- Enchaînement d'accords basée sur trois “petits déplacements” : Video, et avec la basse virtuelle: Video.
- Rem: vraie musique jouée par Miles Davis, Sam Jones, Hank Jones: Video.
4.2 Les tempéraments
- Un tempérament est un “bon” choix de 12 notes par octave pour accorder un instrument. Il est naturel de choisir ces 12 notes parmi les notes du tonnetz (modulo l'octave). Mai sle tonnetz est infini, donc ce choix est arbitraire. Un choix “raisonable” de tempérament est un tempérament contenat des intervalles justes “importants” ou “utiles”.
- Exemples:
- Johannes Kepler, “ Harmonies mundi” 1619. Video

- J.J. Rousseau“Dictionnaire de la musique” 1768. Video

- Tempérament de cloches chinoises de 433 B.C. (ref: article de Cohn 1997, page 63, et Falkenhausen, “suspended music..” p.284 ) Video.

- J.S. Bach, “Clavier bien tempéré”, 1722. (ref: Benson p.188)

- Dans un tempérament juste (non égal), les transpositions donnent des gammes différentes. Conseils de Christian Schubart en 1784:

- Avec Magic Malik en concert le 27/2/2015:


- on a fait des morceaux utilisant le “tempérament des harmoniques” (cercles verts):
Son à 43'', , Video concert, à 30''.
Son: à 7'03'' et 11''10''.
- on a fait des morceaux utilisant le “tempéraments box” sur le réseau (3,5,7)Video

- On définit le tempérament adaptatif: les 12 notes les plus proches des notes principales qui sonnent déjà. Exemple du morceau du concert Video du tonnetz avec basse et sifflet. Son, concert à 6'10'' et 8'10''.
4.3 La gamme pentatonique
- Video de Bobby McFerrin sur l'universalité de la gamme pentatonique (colloque notes&neurons 2009)
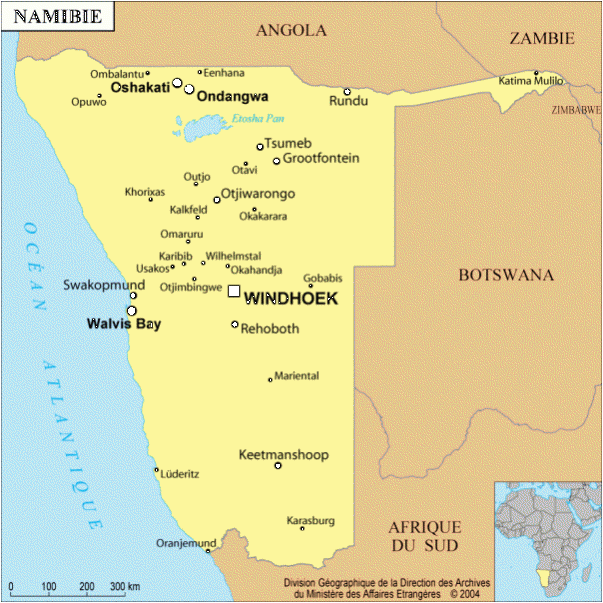
- Gamme pentatonique mineure en namibie, D,F,G,A,C, ref: carnet de voyage avec Emmanuelle Olivier. Son

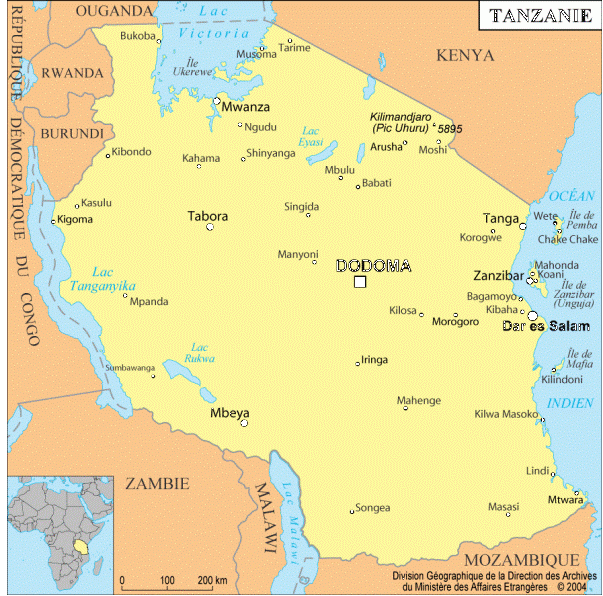
- Carnet voyages avec Pollo Vallejo, wagogo tanzanie, Rituel d'initiation. à 7'25”: gamme pentatonique sur G,A,B,D,F avec le F qui est en 7/8. Son

- Interprétation sur le tonnetz?
- Gamme pentatonique majeure sur le tonnetz: C,E,F,G,Bb Video
- Gamme pentatonique mineure sur le tonnetz: C,Eb,F,G,Bb Video.
Résumé:
- Il pourrait être interessant d'utiliser le tonnetz pour mettre en valeur les relations entre les notes d'un morceau, ou pour interpréter les notes et les accords d'un morceau.
- Comment analyser l'harmonie dans cette oeuvre de Olivier Messian 1930, “offrandes oubliées” Video à 5'47''?

5 Et le rythme?
Il y a aussi incontestablement le rôle de l'arithmétique dans le rythme.
- Musique Zimbabwe. Analyser la polyrythmie à 57mn. Faire ecouter des rapports de rythme en a/b puis sur le tonnetz.
- Faire ecouter, sur hydrogen: découpages en 1,2,3,4,5,6,7 puis seulement 4,5,6 (idem triade majeure) puis 10,12,15 (idem triade mineure).
- Rythmes 7/8 ou 11/8 de roumanie.
- Take 5: 3+2.
- Pour la blague: un rythme 3/2 accéléré donne une quinte.
6 Annexe
6.1 Le verger d'Euclide
Il est naturel de représenter un nombre rationnel positif
par un point
sur le réseau
. La valeur numérique
correspond à la pente de la droite passant par
. Partant de l'origine, le premier couple
que cette droite correspond à une
fraction irréductible. Voir figure
6.1.
- Observations:
- Dessin et explication du verger d'Euclide (orchard visibility problem). Dessin de la fractale des intervalles et comparaison avec la gamme tempérée Dessin des cercles d'appolonius (ou Farey-Stern Brocot). (Rem sur conjecture de Riemann?). On reviendra sur cette fractale avec le tempérament adaptatif.
- Le tempérament égal (division de l'octave en 12 parties égale sur l'echelle log) a plusieurs qualités:
- il approche bien la quarte et la quinte .,
- et en modulant à la quarte ou à la quinte on revient (à peu près) au ton de départ après 12 modulations, car , ou car .
- Le chiffre 12=2*2*3 a beaucoup de diviseurs -> nombreuses gammes symétriques (modes à transposition limité de O. Messian)?
- Ecoute et analyse du chant des peuls (ref et rajouter photos).
- arabe.
Références
1Benson, DJ, "Music: a mathematical offering", Free pdf version on http://homepages.abdn.ac.uk/mth192/pages/html/maths-music.html ().
2Schnupp, Jan and Nelken, Israel and King, Andrew, Auditory neuroscience: Making sense of sound (MIT Press, 2011).