DETAILED PROGRAM HERE
 Algebraic geometry is one of the most central branches of mathematics. It has strong connections with commutative algebra, complex analysis and geometry, topology and number theory, at the very least. Its development has been pursued without interruption from Antiquity, e.g. with the theory of conics and plane curves by the ancien Greeks, to the modern period, which has seen a flourishing of new theories and new connections to other branches of science, and especially physics.
Algebraic geometry is one of the most central branches of mathematics. It has strong connections with commutative algebra, complex analysis and geometry, topology and number theory, at the very least. Its development has been pursued without interruption from Antiquity, e.g. with the theory of conics and plane curves by the ancien Greeks, to the modern period, which has seen a flourishing of new theories and new connections to other branches of science, and especially physics.
The goal of the present Master II programm is to give a wide overview of several central aspects of algebraic geometry, in connection with other related branches of mathematics such as differential geometry and topology. Courses delivered during the first semester are meant to be introductory.
- The course by Philippe Eyssidieux is more algebraic in nature. It introduces the basic dictionary between algebraic varieties and their rings of functions, and then proceeds to discussing singular and regular points and the basic concepts of rational functions and divisors.
- Jean-Pierre Demailly's course has a more analytic focus: the objects under consideration can be similar to those of algebraic geometry, but the tools are borrowed from differential geometry and the theory of holomorphic functions of several variables. In the case of projective varieties, the two approaches have a strong interplay, as exemplified e.g. by Serre's famous GAGA theorem.
- The complex one dimensional case gives rise to theory of Riemann surfaces, initiated by Riemann in the XIXth century, which can also be thought of as real surfaces equipped with a complex structure; this is subject of the course of Louis Funar, Erwan Lanneau and Greg McShane, in which important topological concepts are also introduced (fundamental group, diffeotopies, mapping class group ...)
The second semester offers more advanced material.
- The course by Funar, Lanneau and McShane is a rather direct continuation of the first semester course on surfaces, covering classical topics in the geometry and topology of surfaces and their moduli (moduli spaces are spaces parametrizing possible deformations of a given structure). Applications to the study of geometric structures on low dimensional manifolds will be presented.
- The second advanced course by Jérémy Guéré deals with the enumerative theory of complex curves; to this aim, it also uses the theory of moduli spaces in a crucial manner, along with important theorems such as the Grothendieck-Riemann Roch formula. The theory has strong links with theoretical physics, namely string theory.
- An additional advanced courses might be given during the second semester if there is an
interested audience. Namely a course by Jean Fasel on intersection theory.
PLAN OF THE YEAR
DETAILED PROGRAM HERE
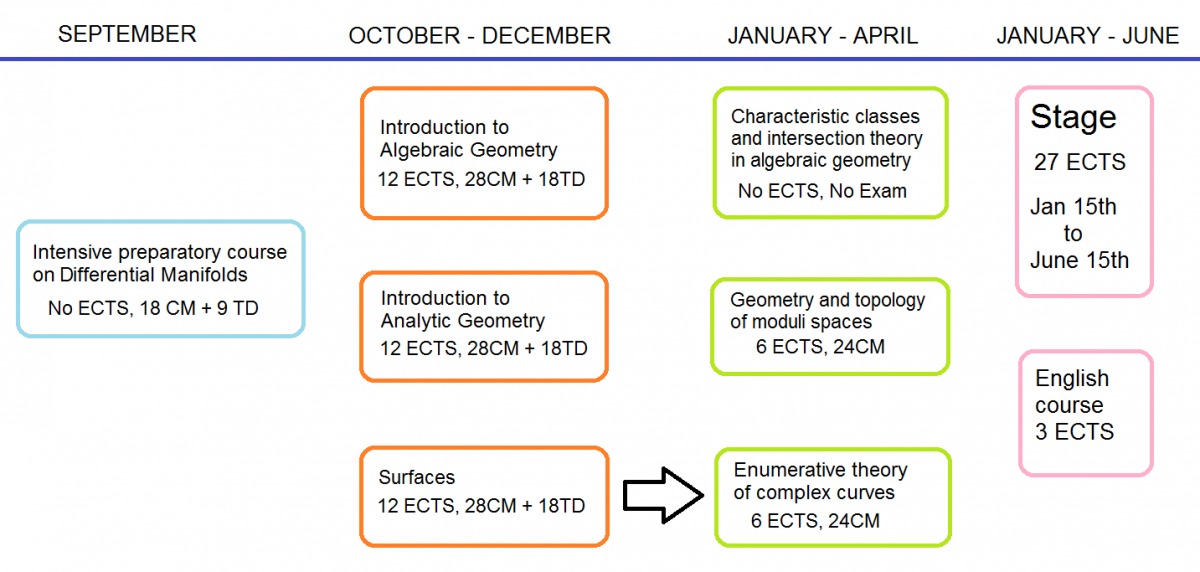
Preparatory course (September)
- Intensive preparatory course on differential manifolds (C.Maclean)
Fundamental courses (October to December with the final exam in the first half of January):
- Introduction to algebraic geometry (P. Eyssidieux)
- Introduction to analytic geometry (J.P. Demailly)
- Surfaces (L.Funar, E.Lanneau, G. Mc Shane, with tutorials by C.Maclean)
Each fundamental course provides each student with 12 ECTS and it comprises 28H of course and 18h of tutorials, i.e. about 5 hours/week
Advanced courses (January to April):
- Geometry and topology of moduli spaces (L.Funar, E.Lanneau, G. Mc Shane)
- Enumerative theory of complex curves (J.Guéré)
Each advanced course provides each student with 6 ECTS and it comprises 24h of course with no tutorials.
Supplementary possible courses (activated if enough students):
This advanced course comprises 24h of course, but it provides NO ECTS and no Exam. It will be activated if enough students will be interested.
In order to obtain the Master 2 degree, students are supposed to respect the following mandatory directives:
- Follow the preparatory course
- Pass at least two of the three fundamental courses
- Pass at least one of the two advanced courses
- Write a ``mémoire" during the stage
- Pass the exam of English language (if the student already has the right level of English, there is no need to pass the English exam).
Further technical description:
The intensive preparatory course take place in thre last three weeks of september, it counts 18H of theory and 12h of tutorials (it does not provide ECTS and there is no exam). Foundamental courses begins in October and finish in December with a final exam in the first half of January. Every fundamental course counts 28 hours of théory and 18h of tutorials (this may change according to the teachers). Globally this takes about 5 hours per week. Usually, the weekly hours of each foundamental course take all place in the same day.
Advanced courses will begin in January, immediately after the exams of the foundamental courses. They require about 2 or 3 months (according to the teachers). Every advanced course counts 24 hours od théory and no tutorials.
The stage also begins just after the exams of January, usually the 15th of January, and it finishes 5 months later in the middle of June.
Note : Students may replace one of these courses with another of a different Master 2 (this needs no timetable conflict and approval by the administration). See for instance the pages of Lyon's Master 2 degree.