Représentation d'une onde dans l'espace de phase

En mécanique classique, l'état d'une particule est caractérisé par un point dans l'espace de phase:

$\displaystyle \textrm{Etat classique }=\left(\textrm{position }x, \textrm{ET vitesse v}\right)$

Alors qu'une onde est spécifiée par ses valeurs $\psi\left(x\right)$ pour chaque position,

OU ses valeurs $\tilde{\psi}\left(p\right)$ pour chaque impulsion , par transformée de Fourier:

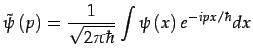
$\displaystyle \tilde{\psi}\left(p\right)=\frac{1}{\sqrt{2\pi\hbar}}\int\psi\left(x\right)e^{-ipx/\hbar}dx$

D'un point de vue mécanique, il serait préférable de lui associer une fonction sur l'espace de phase $\Phi\left(x,p\right)$ .

Analogie avec la musique:

Une onde acoustique est une fonction $\psi\left(t\right)$ du temps .

Ses fréquences sont obtenues par transformée de Fourier:

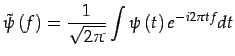
$\displaystyle \tilde{\psi}\left(f\right)=\frac{1}{\sqrt{2\pi}}\int\psi\left(t\right)e^{-i2\pi tf}dt$

Analogie: on remplace $x\Leftrightarrow t$ , $\qquad\left(p=mv\right)/2\pi\hbar\Leftrightarrow f$ .
En musique, fréquence $f\equiv$ hauteur de note. Ex: $445Hz\equiv$ La.
D'un point de vue musical, il serait préférable d'associer à $\psi\left(t\right)$ une fonction sur l'espace temps-fréquences $\Phi\left(x,f\right)$ . Ainsi un fort signal en $\Phi\left(x,f\right)$ signifie que la note de fréquence a été entendue à la date . C'est en effet ainsi que l'on percoit la musique.

Solution:

faire une transformée de Fourier ``fenétrée'' de largeur $\sigma$ petite en temps, autour de la date :

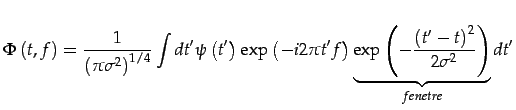
$\displaystyle \Phi\left(t,f\right)=\frac{1}{\left(\pi\sigma^{2}\right)^{1/4}}\i... ...brace{\exp\left(-\frac{\left(t'-t\right)^{2}}{2\sigma^{2}}\right)}_{fenetre}dt'$

De même pour la mécanique quantique, on utilisera:

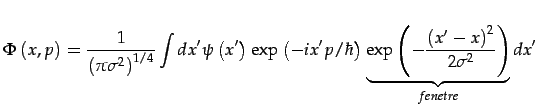
$\displaystyle \Phi\left(x,p\right)=\frac{1}{\left(\pi\sigma^{2}\right)^{1/4}}\i... ...brace{\exp\left(-\frac{\left(x'-x\right)^{2}}{2\sigma^{2}}\right)}_{fenetre}dx'$

Le principe d'incertitude:

L'information du signal $\psi\left(t\right)$ OU $\tilde{\psi}\left(f\right)$ est envoyée en $\Phi\left(t,f\right)$ . Il y a donc une redondance d'information inévitable.

Cela se traduit par le principe d'incertitude:

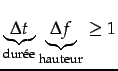
$\displaystyle \underbrace{\Delta t}_{\textrm{durée}}\underbrace{\Delta f}_{\textrm{hauteur}}\geq1$

$\includegraphics[scale=0.6]{paquet_onde_tf}$

En musique: la hauteur de la note est mal défini si elle est courte. Cela s'entend bien dans le grave: si , et $\Delta t=0.2s$ alors $\Delta f>1/2\textrm{ton}$ .

Ainsi en mécanique quantique, avec la correspondance $t\equiv x$ , $f\equiv\frac{p}{2\pi\hbar}=\frac{mv}{2\pi\hbar}$ , cela donne

$\includegraphics[scale=0.6]{paquet_onde_qp}$

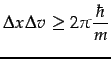
$\displaystyle \Delta x\Delta v\geq2\pi\frac{\hbar}{m}$

i.e. $\Delta x$ petit $\rightarrow\Delta v$ grand, et $\Delta v$ petit $\rightarrow\Delta x$ grand. Dans tous les cas, l'onde ne peut pas rester localisée (ce qui nécéssiterait $\Delta x$ petit et $\Delta v$ petit). L'onde se disperse.

Dispersion de l'onde en régime libre (régulier)

Valeurs numériques pour $\Delta x\Delta v\geq2\pi\frac{\hbar}{m}$ :

avec $\hbar=6.6 10^{-34}J.s$

Pour un électron (libre) $m=9 10^{-31}kg$ , $\qquad$ $\left(\hbar/m\right)=10 cm^{2}/s$
Donc les effets ondulatoires peuvent être de taille macroscopique pour l'électron. (si pas de décohérence).
Pour la Lune (libre) $m=7.10^{22}kg$ $\qquad$ $\left(\hbar/m\right)=10^{-56}m^{2}/s$
Les effets ondulatoires ne peuvent pas atteindre une taille macroscopique en des temps raisonnables.

On verra que le chaos invalide cette conclusion, faite ici pour une particule libre.

Dispersion de l'onde en régime chaotique:

Supposons une dynamique chaotique avec une sensibilité aux conditions initiales: $\Delta x\left(t\right)\simeq\Delta x\left(0\right)10^{t/\tau}$ avec $\tau\simeq1s.$

Exemple: boule de loto:

$\displaystyle \Delta x\left(0\right)\Delta v\left(0\right)\geq\hbar/m\sim10^{-36}m^{2}/s$

Alors au mieux: $\Delta x\left(0\right)\simeq10^{-18}m$ , $\Delta v\left(0\right)\simeq10^{-18}m/s$ .
alors $\Delta x\left(t\right)\simeq1m$ après le temps d'Erhenfest $t\simeq18 s$ qui est très court!

Donc pour un objet macroscopique ayant une dynamique chaotique, l'incertitude quantique peut rapidement atteindre la taille de l'objet.

L'onde n'apparait pas à notre échelle, car la décohérence intervient bien avant. Mais cela montre que pour les phénomènes chaotiques, le hasard quantique a une influence à notre échelle.

Frederic Faure, UJF Grenoble