- Pour un système dynamique hyperbolique
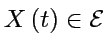 ,
Dans l'espace de phase
,
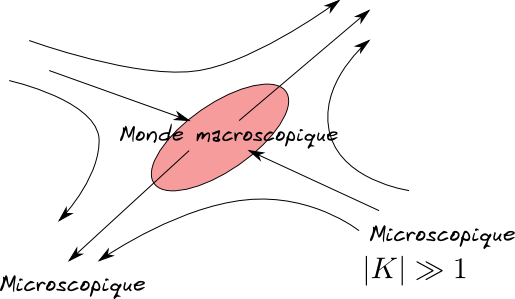
Dans l'espace de phase 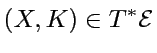 le
``monde macroscopique'' est comme un centre diffuseur
(ens. captif), et l'information fuit hors notre
observation
vers les modes microscopiques (
le
``monde macroscopique'' est comme un centre diffuseur
(ens. captif), et l'information fuit hors notre
observation
vers les modes microscopiques (
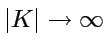 ).
).
- Cette fuite se décrit précisément par une
dynamique effective
linéaire avec un opérateur de Transfert ayant un spectre
discret de résonances. Analogie avec la mécanique ondulatoire.
- A partir de cette description spectrale, on peut déduire plusieurs
caractéristiques importantes: taux de
croissance de l'entropie
(Kolmogorov-Sinaï), le comportement aléatoire des
observables
(théorème central limite et théorie des grandes variations), les
constantes
de diffusion, dimension fractale de l'ens. captif ... et surement
d'autres. Il y a des formules semi-classiques
exactes (formule
de Trace de Atiyah-Bott en terme d'orbites périodiques, ...).
- Noter: dans la nature, le hasard quantique se manifeste à petite
échelle
mais a donc une influence certaine sur l'imprévisibilité des phénomènes
macroscopiques.
- D. Ruelle. ``Turbulence, strange
attractors, and chaos''.
World Scientific Series on Nonlinear Science. Series A. 16. Singapore:
World Scientific, 1995.
- P. Gaspard. ``Chaos, Scattering and
Statistical Mechanics''
Cambridge University Press (1998).
- F. Faure, N. Roy and J. Sjöstrand, Semi-classical
approach for Anosov diffeomorphisms and Ruelle resonances,
Open Math. Journal, vol. 1, 35-81, (2008).
Frederic Faure, UJF Grenoble
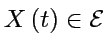 ,
Dans l'espace de phase
,
Dans l'espace de phase 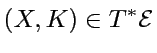 le
``monde macroscopique'' est comme un centre diffuseur
(ens. captif), et l'information fuit hors notre
observation
vers les modes microscopiques (
le
``monde macroscopique'' est comme un centre diffuseur
(ens. captif), et l'information fuit hors notre
observation
vers les modes microscopiques (
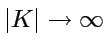 ).
).
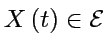 ,
Dans l'espace de phase
,
Dans l'espace de phase 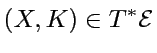 le
``monde macroscopique'' est comme un centre diffuseur
(ens. captif), et l'information fuit hors notre
observation
vers les modes microscopiques (
le
``monde macroscopique'' est comme un centre diffuseur
(ens. captif), et l'information fuit hors notre
observation
vers les modes microscopiques (
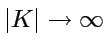 ).
).
