


Next: About this document ...
Up: miastp89_2003
Previous: Noyau et vecteurs isotropes
Exercice Q4 (à rendre à la fin de la séance 9)
On souhaite écrire une fonction gaussdecomp(q,x)
prenant en argument une forme quadratique
q et la liste de variables x dont elle dépend et renvoyant
une expression égale à q écrite comme somme/différence
de carrés indépendants. On va le faire récursivement.
Si x est de longueur 0 ou 1, que faut-il renvoyer?
Sinon, on calcule
aii = 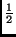
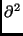 q/
q/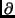 xi2 pour tous
les xi de la liste x:
xi2 pour tous
les xi de la liste x:
- Si on en trouve un aii non nul,
on va s'en servir pour former un carré. On calcule
bi =
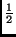
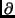 q/
q/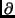 xi. En utilisant
xi. En utilisant
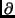 bi/
bi/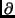 xi = aii, montrer que
q' = q -
xi = aii, montrer que
q' = q - 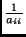 bi2 ne dépend pas de xi. On renvoie alors
bi2 ne dépend pas de xi. On renvoie alors
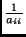 bi2 + gaussdecomp(q', x')
où x' est la liste x dont on a supprimé le i-ième élément
(vous pouvez utiliser
la fonction simplify pour simplifier l'expression de q' avant
l'appel récursif).
bi2 + gaussdecomp(q', x')
où x' est la liste x dont on a supprimé le i-ième élément
(vous pouvez utiliser
la fonction simplify pour simplifier l'expression de q' avant
l'appel récursif).
- Si tous les aii sont nuls, il n'y a pas de termes carrés, on
cherche alors un
aij =
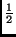
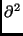 q/
q/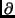 xi
xi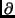 xj
non nul
(s'il n'y en a pas, q est nul et on renvoie 0). Construire alors
une différence de deux carrés qui élimine les variables xi et xj
de q (on pourra utiliser aij, bi et bj).
xj
non nul
(s'il n'y en a pas, q est nul et on renvoie 0). Construire alors
une différence de deux carrés qui élimine les variables xi et xj
de q (on pourra utiliser aij, bi et bj).
Écrire la fonction gaussdecomp.
Exercice Q5 (à rendre à la fin de la séance 9)
Tester le programme précédent pour trouver une base orthogonale
relativement à q lorsque :
q(x) = x12 + 4x1x2 + 2x1x3 - 2x2x3 pour
x = (x1, x2, x3) 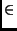
 3
3
Exercice Q6 (à rendre au début de la séance 10)
Soit pour
a 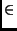
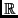 la forme quadratique définie par :
la forme quadratique définie par :
qa(x) = x12 + 3x22 + ax32 - 2x1x2 + 2x1x3 pour
x 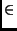
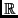 3
3
a/ Écrire la matrice Ma de qa relativement à la base canonique de
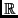 3.
3.
b/ Utiliser le programme précédent pour décomposer qa
comme combinaison
linéaire de carrés de formes linéaires indépendantes.
Expliciter les formes linéaires trouvées.
Pour quelles valeurs de a, qa est-elle : non dégénérée ? définie
positive ?
c/ Dans le cas où qa est définie positive,
montrer qu'il existe une matrice carrée d'ordre 3 Sa telle que :
Ma = tSaSa



Next: About this document ...
Up: miastp89_2003
Previous: Noyau et vecteurs isotropes
Bernard Parisse
2004-06-04
![]()
![]() 3
3
![]()
![]() la forme quadratique définie par :
la forme quadratique définie par :
![]()
![]() 3
3
![]() 3.
3.