Matrice d'une forme quadratique

Exercice Q1 (à rendre fin de la séance 8)
Écrire une fonction est_constant(q,l) qui vérifie qu'une expression q dépendant de plusieurs variables est constante par rapport à la liste l de ces variables (i.e. toutes les dérivées partielles sont nulles). Par exemple pour q:=a+1 et l:=[x1,x2], est_constant doit renvoyer vrai. Rappel: nops(l) donne la taille d'une liste l, et diff(f,x) calcule la dérivée de f par rapport à x

Écrire une fonction est_lineaire(q,l) qui renvoie la matrice de q sous forme d'une liste si q est l'expression d'une forme linéaire par rapport à la liste de variables l et renvoie 0 sinon (indication: on pourra tester que les dérivées partielles sont constantes et utiliser la fonction subs(q,l[i]=0) (MuPAD/xcas) ou subs(l[i]=0,q) (maple) qui permet de remplacer l[i] par 0 dans l'expression q).

Écrire une fonction qui vérifie qu'une expression q dépendant des variables d'une liste l est une forme quadratique et renvoie alors sa matrice ou renvoie 0 sinon. Tester avec q:=x1^2+2*x1*x2 et l:=[x1,x2].
Indication: On remarquera qu'une expression est quadratique en l:=[x1,...,xn]; si elle vaut zéro en (x₁,..., x_n) = (0,..., 0) et si ses dérivées partielles sont des formes linéaires.

Exercice Q2 (à rendre au début de la séance 9)
On considère dans 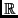$\mathbb {R}$⁴ la forme quadratique :
q(x) = - (x₁ + 5x₂ + x₃ - x₄)² + 3(x₁ - x₂ - 2x₃)² + (x₄ + x₂ + 2x₃)²
Écrire la forme bilinéaire symétrique f, forme polaire de q .
Écrire la matrice associée à f dans la base canonique.
Tester la fonction de l'exercice Q1 avec q, q + 1 et x1³.