


Next: Algorithme de Héron
Up: Complément de cours
Previous: Théorème du point fixe
Pour résoudre l'équation 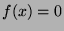 , on itère la fonction :
, on itère la fonction :
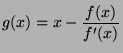 .
.
Puisque
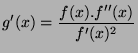 ,
si
,
si 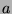 est un zéro de
est un zéro de 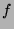 , on a :
, on a :
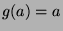 ,
, 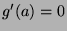 et la suite des itérées de
et la suite des itérées de 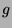 (
(
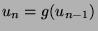 ) converge de façon quadratique (
) converge de façon quadratique (
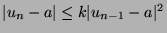 ).
).
Cette méthode
nécessite de partir d'un point assez proche de la racine.
2003-02-19
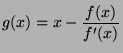 .
.
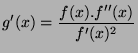 ,
si
,
si