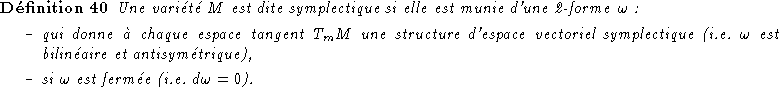
Exemple fondemental:
Preuve
Soit 
la projection canonique de T*X sur X définie par:
Cette projection est une application 
donc admet une application
linéaire tangente:
A l'aide de cette application linéaire tangente, on définit la 1-forme
canonique 
sur T*X (c'est une section de T*(T*X)) par:
La structure symplectique de T*X est alors donnée par la 2-forme:
L'antisymétrie de 
est évidente, de même que le fait
que 
. Il reste à vérifier que est non
dégénéré.
On choisit un système de coordonnées locales (x1,...,xn), soit
la base correspondante de T*xX, et
les coordonnées de la forme
dans cette base.
Soit 
. On a:
donc:
d'où:
ce qui signifie que pour deux vecteurs v et v' de 
de coordonnées (q,p) et (q',p'), on a:
qui est la forme canonique d'une forme bilinéaire antisymétrique non dégénérée.
Exemple de sous-variété lagrangienne de T*X
Soit 
une fonction et:
C'est une sous-variété de dimension n de T*X (où
n=dimX) qui est le graphe de 
. La fonction
est appelée fonction génératrice de la variété
.
Montrons que 
est lagrangienne. En coordonnées
locales, 
si
qui est l'équation
d'un sous-espace vectoriel de dimension n=dimT*X/2, de plus
est isotrope car:
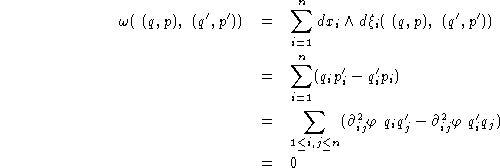
Plus généralement, 
où 
est une 1-forme
est lagrangienne si 
. Localement, une telle
sous-variété est de la forme . En fait, pour
qu'une sous-variété lagrangienne soit localement le graphe d'une
différentielle de fonction, il suffit que la projection canonique
restreinte à Y soit un difféomorphisme local de Y sur X.
Caractérisation:
On munit 
de la 2-forme 
:
ce qui en fait une variété symplectique.
Alors est canonique si et seulement si le graphe Y de
est une sous-variété lagrangienne de .
En effet:
Comme Y a la dimension d'une variété lagrangienne, il suffit de vérifier que:
Or
si et seulement si:
i.e. si et seulement si 
donc si et seulement si est canonique.
