


suivant: Types composÚs.
monter: Les réels
précédent: Erreurs
Index
On a vu précédemment que pour représenter un réel, on devait
l'arrondir, ce qui introduit une erreur même si le réel est
connu exactement (par exemple 1/10).
Voyons comment se propagent les erreurs
dans les opérations arithmétiques
de base : on distingue l'addition, la multiplication
et l'inversion. La soustraction se ramène à l'addition car
le calcul de l'opposé n'introduit aucune erreur nouvelle.
Pour l'addition, si
| x - x0| 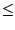
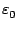 et si
| y - y0|
et si
| y - y0| 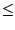
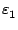 alors par l'inégalité triangulaire (
| a + b|
alors par l'inégalité triangulaire (
| a + b| 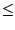 | a| + | b|), on a :
| a| + | b|), on a :
|(
x +
y) - (
x0 +
y0)|
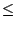
|
x -
x0| + |
y -
y0|
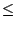
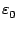
+
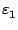
Définition 1
L'erreur absolue
est définie comme un majorant de la valeur absolue
de la différence entre le nombre réel et
son représentant double :
|
x -
x0|
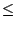
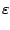
Mais comme il faut représenter x0 + y0
en machine, on doit ajouter une erreur d'arrondi, qui est
proportionnelle à la valeur absolue de x0 + y0 d'où la notion
d'erreur relative :
Définition 2
L'erreur relative est égale à l'erreur absolue divisée par
la valeur absolue du nombre
|
x -
x0|
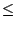
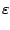
|
x0|
Remarquons au passage que les erreurs de mesure expérimentales sont
pratiquement toujours des erreurs relatives.
Donc lorsqu'on effectue une addition (ou une soustraction) de deux réels
sur machine, on doit additionner les deux erreurs absolues sur les opérandes
et ajouter une erreur d'arrondi (relative de 2-53, à titre
d'exercice, on pourra vérifier que cette erreur
d'arrondi est majorée par l'erreur absolue de la somme x + y dès l'instant où
x et y ont eux-même une erreur d'arrondi).
Lorsqu'on effectue une multiplication de deux nombres x, y dont les
représentants x0, y0 sont non nuls, on a
l'erreur relative est donc la somme des erreurs relatives et du produit
des erreurs relatives (on peut souvent négliger le produit devant la somme). Il
faut aussi y ajouter une erreur relative d'arrondi de 2-53 sur x0y0.
On observe que la multiplication est une opération posant moins
de problèmes que l'addition, car on manipule toujours des erreurs
relatives, par exemple si l'erreur relative sur deux doubles
x et y non nuls
est de 2-53, alors l'erreur relative sur xy sera de
2
-53 +2
-53 +2
-106 +2
-53 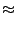
3×2
-53
Une autre conséquence importante est que l'addition de réels sur machine
n'est pas une opération associative,
par exemple
(2.0
-53 +2.0
-53) + 1.0
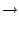
1 + 2
-52
(2.0
-53 +1.0) + 2.0
-53 
1
Exercice : pour calculer la valeur
numérique d'une dérivée de fonction, il vaut mieux
calculer
(f (x + h) - f (x - h))/(2h) que
(f (x + h) - f (x))/h. Attention
à ne pas prendre h trop petit, sinon x + h = x.
Remarquons néanmoins que les erreurs calculées ici sont des majorations
des erreurs réelles (ou si on préfère l'erreur obtenue dans le pire
des cas), statistiquement les erreurs sur les résultats sont moindres.
Il est d'ailleurs souvent trop difficile de calculer la majoration
rigoureuse de l'erreur pour des calculs complexes.
Lorsqu'on doute de la précision d'un calcul, un test peu couteux consiste
à refaire ce calcul en utilisant des flottants en précision plus
grande et tester si le résultat varie en fonction du nombre de chiffres
significatifs utilisés. On peut aussi faire varier légèrement
les données et observer la sensibilité du résultat.
Si on veut travailler en toute rigueur sans
pour autant calculer les erreurs à priori, il faut utiliser un logiciel
utilisant des intervalles pour représenter les réels (par exemple
la bibliothèque C MPFI).



suivant: Types composÚs.
monter: Les réels
précédent: Erreurs
Index
Retour à la page principale de mat249