


suivant: Itérations inverses
monter: Réduction approchée des endomorphismes
précédent: Réduction approchée des endomorphismes
Index
Méthode de la puissance
Elle permet de déterminer la plus grande valeur propre en valeur absolue
d'une matrice diagonalisable lorsque celle-ci est unique.
Supposons en effet que les valeurs propres de A soient
x1,..., xn avec
| x1| 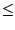 | x2|
| x2| 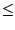 ...
... 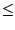 | xn-1| < | xn|
et soient
e1,..., en une base de vecteurs propres correspondants.
On choisit un vecteur aléatoire v et on calcule la suite
vn = Avn-1 = Anv. Si v a pour coordonnées
V1,..., Vn)
dans la base propre, alors
| xn-1| < | xn|
et soient
e1,..., en une base de vecteurs propres correspondants.
On choisit un vecteur aléatoire v et on calcule la suite
vn = Avn-1 = Anv. Si v a pour coordonnées
V1,..., Vn)
dans la base propre, alors
vn =
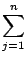 Vjxjnej
Vjxjnej =
xnnwn,
wn =
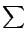 Vj
Vj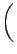
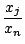
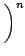 ej
ej
L'hypothèse que xn est l'unique valeur propre
de module maximal entraine alors
que
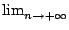 wn = Vnen puisque la suite
géométrique de raison xj/xn converge vers 0.
Autrement dit, si Vn
wn = Vnen puisque la suite
géométrique de raison xj/xn converge vers 0.
Autrement dit, si Vn 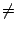 0 (ce qui a une probabilité 1 d'être
vrai pour un vecteur aléatoire),
vn est équivalent à
Vnxnnen. Lorsque n
est grand, vn est presque colinéaire au vecteur propre
en (que l'on peut prendre comme vn divisé par sa norme),
ce que l'on détecte en testant si vn+1 et vn
sont presques colinéaires, et de plus le facteur de colinéarité
entre vn+1 et vn est presque xn, la valeur propre
de module maximal.
0 (ce qui a une probabilité 1 d'être
vrai pour un vecteur aléatoire),
vn est équivalent à
Vnxnnen. Lorsque n
est grand, vn est presque colinéaire au vecteur propre
en (que l'on peut prendre comme vn divisé par sa norme),
ce que l'on détecte en testant si vn+1 et vn
sont presques colinéaires, et de plus le facteur de colinéarité
entre vn+1 et vn est presque xn, la valeur propre
de module maximal.
Exercice : tester la convergence de Anv vers l'espace propre
associé à 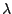 = 3 pour la matrice
= 3 pour la matrice [[1,-1],[2,4]]
et le vecteur (1, 0).
Lorsqu'on applique cette méthode a une matrice réelle, il peut arriver
quíl y ait deux valeurs propres conjuguées de module maximal. Le même
type de raisonnement montre que pour n grand,
vn+2 est presque colinéaire à l'espace engendré par vn et vn+1,
la relation
vn+2 + xvn+1 + x2vn = 0 permet de calculer les
valeurs propres.
La convergence est de type série géométrique, on gagne le même nombre
de décimales à chaque itération.



suivant: Itérations inverses
monter: Réduction approchée des endomorphismes
précédent: Réduction approchée des endomorphismes
Index
Retour à la page principale de mat249
![]() = 3 pour la matrice
= 3 pour la matrice