


suivant: Polynome minimal
monter: Réduction exacte des endomorphismes
précédent: Réduction exacte des endomorphismes
Index
Polynome caractéristique
On peut le calculer en développant le déterminant det
A - 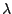 I, mais
il est plus efficace de le calculer par interpolation.
Soit A une matrice carrée de taille n,
on sait que son polynome caractéristique
est un polynome de degré n, il suffit
de connaitre sa valeur en n + 1 points distincts, on calcule
donc n + 1 déterminants det
A -
I, mais
il est plus efficace de le calculer par interpolation.
Soit A une matrice carrée de taille n,
on sait que son polynome caractéristique
est un polynome de degré n, il suffit
de connaitre sa valeur en n + 1 points distincts, on calcule
donc n + 1 déterminants det
A - 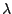 I en remplaçant
I en remplaçant 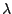 par
sa valeur (il y a plus de déterminants à calculer mais
ce sont des déterminants sans paramètre
par
sa valeur (il y a plus de déterminants à calculer mais
ce sont des déterminants sans paramètre 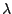 donc beaucoup
plus simple à calculer), ce qui permet de reconstruire le polynome
caractéristique par interpolation de Lagrange.
donc beaucoup
plus simple à calculer), ce qui permet de reconstruire le polynome
caractéristique par interpolation de Lagrange.
Exercice : pour [[1,-1],[2,4]], calculer
det
(A - 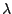 I) en
I) en
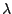 = 0, 1, 2 puis le polynome d'interpolation,
vérifier que c'est bien le polynome caractéristique.
= 0, 1, 2 puis le polynome d'interpolation,
vérifier que c'est bien le polynome caractéristique.
Il faut effectuer n + 1 calculs de déterminants, ce qui nécessite
O(n4) opérations. Il existe des méthodes plus efficaces, par
exemple le calcul du polynome minimal probabiliste présenté
plus bas (O(n3) opérations).
Retour à la page principale de mat249
![]() I) en
I) en
![]() = 0, 1, 2 puis le polynome d'interpolation,
vérifier que c'est bien le polynome caractéristique.
= 0, 1, 2 puis le polynome d'interpolation,
vérifier que c'est bien le polynome caractéristique.