


suivant: Applications de Gauss
monter: Le pivot de Gauss
précédent: Efficacité de l'algorithme
Index
Erreurs d'arrondis du pivot de Gauss
Comme
| ajc| 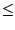 | alc|, une étape de réduction multiplie
au plus l'erreur absolue des coefficients par 2. Donc la
réduction complète d'une matrice peut multiplier au pire l'erreur
absolue sur les coefficients par 2n (où n est le nombre
d'étapes de réduction, inférieur au plus petit du nombre de lignes
et de colonnes). Ceci signifie qu'avec la précision d'un double,
on peut au pire perdre toute précision pour des matrices pas
si grandes que ça (n = 52). Heureusement, il semble qu'en pratique,
l'erreur absolue
ne soit que très rarement multipliée par un facteur supérieur à 10.
| alc|, une étape de réduction multiplie
au plus l'erreur absolue des coefficients par 2. Donc la
réduction complète d'une matrice peut multiplier au pire l'erreur
absolue sur les coefficients par 2n (où n est le nombre
d'étapes de réduction, inférieur au plus petit du nombre de lignes
et de colonnes). Ceci signifie qu'avec la précision d'un double,
on peut au pire perdre toute précision pour des matrices pas
si grandes que ça (n = 52). Heureusement, il semble qu'en pratique,
l'erreur absolue
ne soit que très rarement multipliée par un facteur supérieur à 10.
Par contre, si on ne prend pas la précaution de choisir le pivot
de norme maximale dans la colonne, les erreurs d'arrondis se
comportent de manière bien moins bonnes, cf. l'exemple suivant.
Exemple
Soit à résoudre le système linéaire
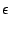 x
x + 1.0
y = 1.0,
x + 2.0
y = 3.0
avec
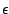 = 2-54 (pour une machine utilisant des doubles pour
les calculs en flottant,
plus générallement on choisira
= 2-54 (pour une machine utilisant des doubles pour
les calculs en flottant,
plus générallement on choisira 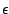 tel que
(1.0 + 3
tel que
(1.0 + 3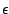 ) - 1.0
soit indistinguable de 0.0).
) - 1.0
soit indistinguable de 0.0).
Si on résoud le système exactement,
on obtient
x = 1/(1 - 2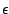 ) (environ 1)
et
y = (1 - 3
) (environ 1)
et
y = (1 - 3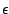 )/(1 - 2
)/(1 - 2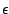 ) (environ 1).
Supposons que l'on n'utilise pas la stratégie du pivot partiel,
on prend alors comme pivot
) (environ 1).
Supposons que l'on n'utilise pas la stratégie du pivot partiel,
on prend alors comme pivot 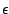 , donc on effectue la
manipulation de ligne
L2
, donc on effectue la
manipulation de ligne
L2 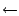 L2 -1/
L2 -1/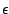 L1 ce qui
donne comme 2ème équation
(2.0 - 1.0/
L1 ce qui
donne comme 2ème équation
(2.0 - 1.0/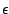 )y = 3.0 - 1.0/
)y = 3.0 - 1.0/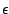 .
Comme les calculs sont numériques, et à cause des erreurs
d'arrondis, cette 2ème équation sera remplacée par
(- 1.0/
.
Comme les calculs sont numériques, et à cause des erreurs
d'arrondis, cette 2ème équation sera remplacée par
(- 1.0/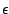 )y = - 1.0/
)y = - 1.0/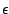 d'où y = 1.0, qui sera remplacé
dans la 1ère équation, donnant
d'où y = 1.0, qui sera remplacé
dans la 1ère équation, donnant
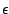 x = 1.0 - 1.0y = 0.0 donc
x = 0.0.
x = 1.0 - 1.0y = 0.0 donc
x = 0.0.
Inversement, si on utilise la stratégie du pivot partiel, alors
on doit échanger les 2 équations L2' = L1 et L1' = L2 puis on effectue
L2 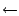 L2' -
L2' - 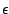 L1', ce qui donne
(1.0 - 2.0
L1', ce qui donne
(1.0 - 2.0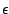 )y = 1.0 - 3.0
)y = 1.0 - 3.0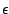 , remplacée en raison
des erreurs d'arrondi par 1.0*y = 1.0 donc y = 1.0, puis on remplace
y dans L1' ce qui donne
x = 3.0 - 2.0y = 1.0.
, remplacée en raison
des erreurs d'arrondi par 1.0*y = 1.0 donc y = 1.0, puis on remplace
y dans L1' ce qui donne
x = 3.0 - 2.0y = 1.0.
On observe dans les deux cas que la valeur de y est proche de la
valeur exacte, mais la valeur de x dans le premier cas est
grossièrement eloignée de la valeur correcte.
On peut aussi s'intéresser à la sensibilité de la solution d'un
système linéaire à des variations de son second membre. Le traitement
du sujet à ce niveau est un peu difficile, cela fait intervenir
le nombre de conditionnement de la matrice A du système (qui
est essentiellement la valeur absolue du rapport de la valeur propre
la plus grande sur la valeur propre la plus petite), plus
ce nombre est grand, plus la solution variera (donc plus on
perd en précision).



suivant: Applications de Gauss
monter: Le pivot de Gauss
précédent: Efficacité de l'algorithme
Index
Retour à la page principale de mat249