On dit qu'une méthode d'intégration est d'ordre n si il y a égalité ci-dessus pour tous les polynômes de degré inférieur ou égal à n et non égalité pour un polynôme de degré n + 1. Par exemple, les rectangles à droite et gauche sont d'ordre 0, le point milieu et les trapèzes sont d'ordre 1. Plus générallement, si on approche f par son polynôme d'interpolation de Lagrange en n + 1 points (donc par un polynôme de degré inférieur ou égal à n), on obtient une méthode d'intégration d'ordre au moins n.
Si une méthode est d'ordre n avec des wj ![]() 0 et
si f est n + 1 fois continument dérivable,
alors sur une subdivision, on a :
0 et
si f est n + 1 fois continument dérivable,
alors sur une subdivision, on a :
En effet, on fait le développement de Taylor de f par exemple
en ![]() à l'ordre n
à l'ordre n
| f (t) | = | Tn(f )+ 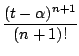 f[n+1]( f[n+1]( |
|
| Tn(f ) | = | f (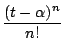 f[n]( f[n]( |
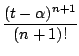 | f[n+1](
| f[n+1](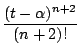
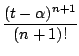

| | |
= | | |
|
| | |
|||
Mn+1 + +  |
Après sommation sur les n subdivisions, on obtient que pour une méthode d'ordre n à coefficients positifs
 (b - a)(
(b - a)(On observe que cette majoration a la bonne puissance de h sur les exemples déja traités, mais pas forcément le meilleur coefficient possible, parce que nous avons traité le cas général d'une méthode d'ordre n.