


suivant: Calcul approché des racines
monter: Factorisation des polynômes
précédent: Multiplicité des racines.
Index
Reste maintenant à trouver des racines!
On a le :
Théorème 9 (d'Alembert)
Soit P un polynome de degré non nul, alors P admet au moins
une racine complexe.
On peut alors factoriser P par X - r si r est la racine, et
recommencer avec le quotient, d'où le corollaire.
Théorème 10
Soit P un polynome de degré n non nul, alors P admet n
racines complexes (comptées avec multiplicité)
x1,..., xn,
on a donc :
P(X) = an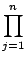 (X - xj) (X - xj) |
(4) |
où an est le coefficient dominant de P.
Démonstration du théorème de d'Alembert :
On va montrer que le minimum de la valeur absolue de P est atteint
en un nombre complexe puis que ce minimum est forcément nul.
Soit
P(
x) =
anxn + ... +
a0,
an 
0
Lorsque | x| tend vers l'infini, | P(x)| tend vers l'infini, en
effet
P(
x) =
anxn(1 +
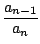
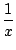
+ ... +
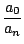

)
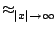 anxn
anxn
plus précisément il existe R > 0 tel que si
| x| > R alors
| P(x)| > | an|| x|n/2. Quitte à augmenter R on
peut donc supposer que
| P(x)| > | P(0)| si | x| > R, donc il existe
un complexe x0 qui réalise le minimum de | P| sur
 (ce
minimum est en fait le minimum pour | x|
(ce
minimum est en fait le minimum pour | x| 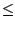 R). On va montrer par
l'absurde que ce minimum est nul (donc que x0 est la racine
cherchée). Supposons donc que
P(x0)
R). On va montrer par
l'absurde que ce minimum est nul (donc que x0 est la racine
cherchée). Supposons donc que
P(x0) 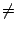 0. On fait le
développement de Taylor de P en x0 à l'ordre n=degré de P, donc
le développement n'a pas de reste :
0. On fait le
développement de Taylor de P en x0 à l'ordre n=degré de P, donc
le développement n'a pas de reste :
P(
x) -
P(
x0) = (
x -
x0)
P'(
x0) + .. + (
x -
x0)
n![$\displaystyle {\frac{{P^{[n]}(x_0)}}{{n!}}}$](img140.png)
Comme P n'est pas constant, l'un des termes du membre de droite est
non nul, soit k l'indice du premier terme non nul, on a alors :
P(
x) =
P(
x0) + (
x -
x0)
k![$\displaystyle {\frac{{P^{[k]}(x_0)}}{{k!}}}$](img141.png)
+
o((
x -
x0)
k)
Comme
P(x0) 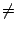 0, on peut le factoriser en :
0, on peut le factoriser en :
P(
x) =
P(
x0)(1 + (
x -
x0)
k![$\displaystyle {\frac{{P^{[k]}(x_0)}}{{P(x_0) k!}}}$](img142.png)
+
o((
x -
x0)
k)
on pose alors x = x0 + tw où w est une racine k-ième (cela
existe dans
 ) de
on a alors :
) de
on a alors :
P(x) = P(x0)(1 - tk + o(tk+1))
lorsque t est positif, suffisamment petit, on a
0 < 1 - tk + o(tk+1 < 1, donc
| P(x)| < | P(x0)|, ce qui est absurde (x0 réalisant
le minimum de P sur
 ).
).
Remarque :
Si on développe la relation (4), on obtient
des relations entre les coefficients du polynome et les racines, par
exemple :
an-1 =
an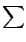 j
j=1
n(-
xj),...,
a0 =
an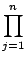
(-
xj),



suivant: Calcul approché des racines
monter: Factorisation des polynômes
précédent: Multiplicité des racines.
Index
Retour à la page principale de mat249
![$\displaystyle {\frac{{P^{[n]}(x_0)}}{{n!}}}$](img140.png)
![$\displaystyle {\frac{{P^{[k]}(x_0)}}{{k!}}}$](img141.png) + o((x - x0)k)
+ o((x - x0)k)
![$\displaystyle {\frac{{P^{[k]}(x_0)}}{{P(x_0) k!}}}$](img142.png) + o((x - x0)k)
+ o((x - x0)k)
![$\displaystyle {\frac{{-P^{[k]}(x_0)}}{{P(x_0) k!}}}$](img144.png)