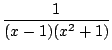


suivant: Factorisation des polynômes
monter: Polyn˘mes : arithmétique, factorisation, interpolation
précédent: Polyn˘mes : arithmétique, factorisation, interpolation
Index
On considère les polynômes à une variable à coefficients
dans
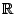 ou
ou
 ou
ou
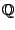 . Les algorithmes de base déjà
évoqués sont l'évaluation en un point (méthode de Horner),
l'addition, la soustraction, la multiplication et la division
euclidienne de A par B
. Les algorithmes de base déjà
évoqués sont l'évaluation en un point (méthode de Horner),
l'addition, la soustraction, la multiplication et la division
euclidienne de A par B 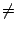 0 :
0 :
A = BQ + R, deg(R) < deg(B)
A l'aide de la division euclidienne, on peut calculer le PGCD de
deux polynômes par l'algorithme d'Euclide. Nous allons présenter
l'algorithme d'Euclide étendu (ou de Bézout)
Théorème 7
Étant donnés 2 polynômes A et B, il existe deux polynômes U,
V tels que
AU + BV = pgcd(A, B), deg(U) < deg(B),deg(V) < deg(A)
Algorithme :
On construit en fait 3 suites (Un), (Vn) et (Rn) telles que :
AUn + BVn = Rn
Exemple :
A = x3 -1, B = x2 + 1, les rangs 0 et 1 sont donnés ci-dessus.
Au rang 2, Q0 est le quotient euclidien de A par B (fonction
quo) donc x, d'où
U2 = 1, V2 = - x, R2 = - x - 1
Puis on divise x2 + 1 par - x - 1, quotient - x + 1, donc
U3 = x - 1, V3 = 1 + x(- x + 1) = 1 + x - x2, R3 = 2
Preuve de l'algorithme :
On montre facilement par récurrence que la relation
AUn + BVn = Rn est conservée. Comme Rn est la suite des restes, le dernier
reste non nul est bien le pgcd de A et B.
D'autre part, examinons les degrés des Vk. Supposons que
deg(A) 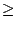 deg(B) (sinon on échange A et B).
Au rang n = 0, V0 = 0 donc
V2 = - Q0V1, aux rangs suivants
le degré de Qn est non nul (car le degré de Rn+1 est
strictement inférieur au degré de Rn)
On montre donc par récurrence que la suite des degrés de Vn
est croissante et que :
deg(B) (sinon on échange A et B).
Au rang n = 0, V0 = 0 donc
V2 = - Q0V1, aux rangs suivants
le degré de Qn est non nul (car le degré de Rn+1 est
strictement inférieur au degré de Rn)
On montre donc par récurrence que la suite des degrés de Vn
est croissante et que :
deg(Vn+2) = deg(Qn) + deg(Vn+1)
Comme deg(Qn)=deg(Rn)-deg(Rn+1), on en déduit que
deg(Vn+2) + deg(Rn+1) = deg(Vn+1) + deg(Rn) = ... = deg(V1) + deg(R0) = deg(A)
Donc si n + 2 est le rang du dernier reste non nul, Vn+2 = V et
degV=degA-degRn+1 est donc strictement
inférieur au degré de A (car Rn+1,
l'avant-dernier reste non nul,
est de degré plus grand ou égal à 1).
On en déduit enfin que le degré de U est strictement
inférieur au degré de B, car AU = R - BV, le degré
de BV est strictement inférieur à celui de B plus
celui de A.
L'identité de Bézout permet de résoudre plus générallement
une équation du type
Au + Bv = C
où A, B, C sont trois polynômes donnés, à condition que
C soit divisible par le pgcd de A et B.
L'ensemble des solutions s'obtient à partir d'une solution
particulière U, V de Bézout, notons
c = C/gcd(A, B),
on a alors
A(cU) + B(cV) = c gcd(A, B) = C
et l'ensemble des solutions est donné par
u = cU - PB, v = cV + PA où P est un polynôme
quelconque.
Si le degré de C est plus petit que le degré de A
plus le degré de B, il existe une solution
``priviligiée'', on prend pour u le reste de la division
euclidienne de cU par B, v est alors le reste
de la division euclidienne de cV par A pour des
raisons de degré.
Exemple : si on veut résoudre
(x3 -1)u + (x2 +1)v = 2x2
on multiplie U = x - 1 et V = 1 + x - x2 par x2 ce qui donne une solution
u = x2(x - 1), v = x2(1 + x - x2)
l'ensemble des solutions est de la forme
u + P(x2 +1), v - P(x3 - 1)
et la solution priviligiée (de degrés minimaux) est
- x + 1 = rem(x2(x - 1), x2 +1), x2 - x + 1 = rem(x2(1 + x - x2), x3 - 1)
L'identité de Bézout intervient dans de nombreux problèmes
en particulier la décomposition en éléments simples d'une fraction
rationnelle. Si le dénominateur D d'une fraction se factorise
en produit de 2 facteurs D = AB premiers entre eux, alors
il existe deux polynômes u et v tels que N = Au + Bv, donc
Si de plus N/D est une fraction propre (degré de N plus petit
que celui de D), alors u/B et v/A sont encore des fractions
propres (en calculant le reste de la division euclidienne pour u et
v comme expliqué ci-dessus).
Par exemple :
Les applications sont diverses, citons
- le calcul de primitive de fraction rationnelles (et tout
ce qui s'y ramène), par exemple
Puis on fait apparaitre la dérivée du dénominateur au numérateur
pour éliminer les x,
2x = (x2 + 1)'
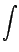 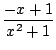 |
= |
- 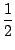 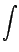 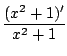 + + 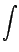 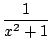 + + 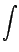 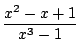 |
|
| |
= |
- 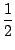 ln(x2 +1) + arctan(x) + ln(x2 +1) + arctan(x) + 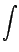 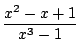 |
|
pour faire le calcul complet, il faut aussi décomposer
la fraction restante (exercice!)
- le calcul de transformée de Laplace inverse de fractions
rationnelles, l'idée est la même, sauf qu'on remplace l'intégrale
par la transformée de Laplace inverse (et les formules donnant
la transformée inverse de 1/(x - p),
1/(x2 + p2),
p/(x2 + p2)
respectivement
exp(px), sin(xp)/p, cos(px))
(calcul non exigible à l'examen)
- le calcul du terme d'ordre n du développement de Taylor
en 0 d'une fraction rationnelle. On décompose, et on se ramène à des
séries dont le terme général est connu, comme
(a + x)-n.
Par exemple pour connaitre le développement de
1/(x2 - 3x + 2),
on factorise le dénominateur
1/((x - 1)(x - 2)), on décompose
et on développe, le terme d'ordre n est donc
1 - (1/2)n+1.
Il faut néanmoins savoir factoriser un polynôme, ce dont nous
parlerons dans la section suivante.
Exercice :
Calculer l'intégrale
en utilisant l'identité de Bézout pour décomposer la fraction rationnelle.
Trouver à l'aide de cette décomposition le terme d'ordre
n du développement de Taylor de la fraction à intégrer, vérifier
avec un logiciel de calcul formel que les termes d'ordre 0 à 3 sont
corrects.
Una autre application est l'élimination dans les systèmes
polynomiaux, par exemple considérons le système de 2 équations
à 2 inconnues (intersection d'une ellipse et d'un cercle) :
x2 + y2 -9 = 0, x2 +2y2 - 2xy - 7 = 0
En calculant les coefficients de Bézout des 2 polynômes en x
x2 + y2 - 9 et
x2 +2y2 - 2xy - 7 et en multipliant au besoin par
le PPCM (plus grand commun multiple) des dénominateurs, on obtient
à droite de l'équation de Bézout un polynôme ne dépendant que
de y et qui s'annule aussi aux solutions du système, on peut alors
résoudre en y (en factorisant) puis en x. Ici par exemple
ce polynome est
5y4 -32y2 + 4.
Cette méthode se systématise, le polynome obtenu par élimination
d'une variable est appelé résultant.



suivant: Factorisation des polynômes
monter: Polyn˘mes : arithmétique, factorisation, interpolation
précédent: Polyn˘mes : arithmétique, factorisation, interpolation
Index
Retour à la page principale de mat249
![]() deg(B) (sinon on échange A et B).
Au rang n = 0, V0 = 0 donc
V2 = - Q0V1, aux rangs suivants
le degré de Qn est non nul (car le degré de Rn+1 est
strictement inférieur au degré de Rn)
On montre donc par récurrence que la suite des degrés de Vn
est croissante et que :
deg(B) (sinon on échange A et B).
Au rang n = 0, V0 = 0 donc
V2 = - Q0V1, aux rangs suivants
le degré de Qn est non nul (car le degré de Rn+1 est
strictement inférieur au degré de Rn)
On montre donc par récurrence que la suite des degrés de Vn
est croissante et que :
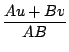 =
= 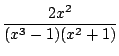 =
= 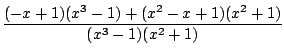 =
= 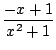 +
+ 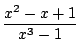
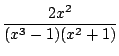 = =
= = 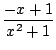 +
+ 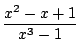
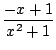
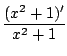 +
+ 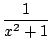 +
+ 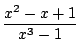
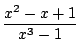
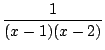 =
=